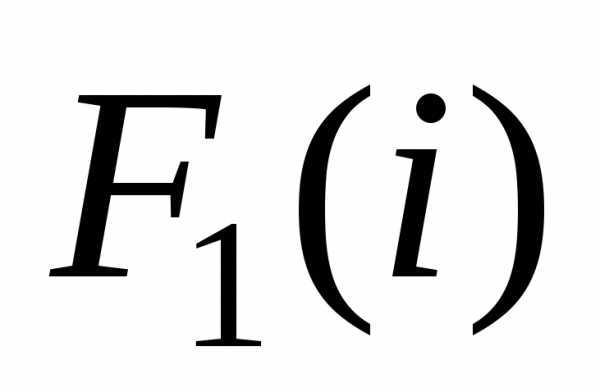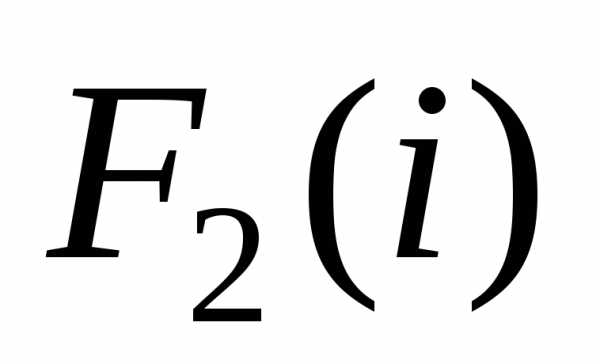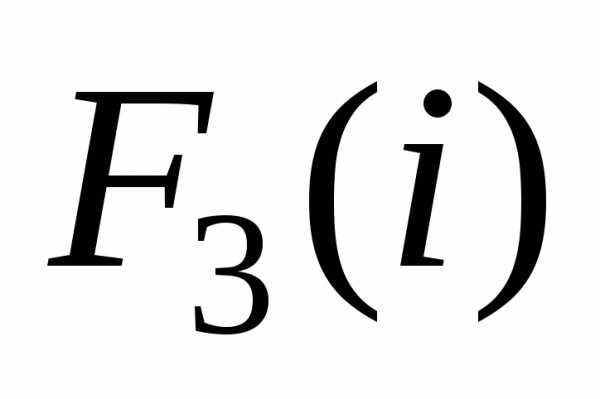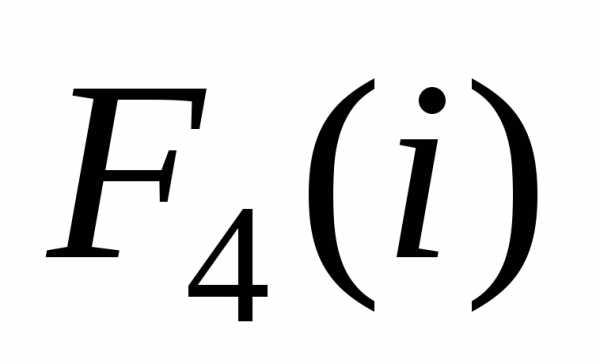Энциклопедия по машиностроению XXL. Последовательность этапов задачи условной оптимизации
I этап. Условная оптимизация.
1-й шаг. k = 6. Для первого шага возможные состояния системы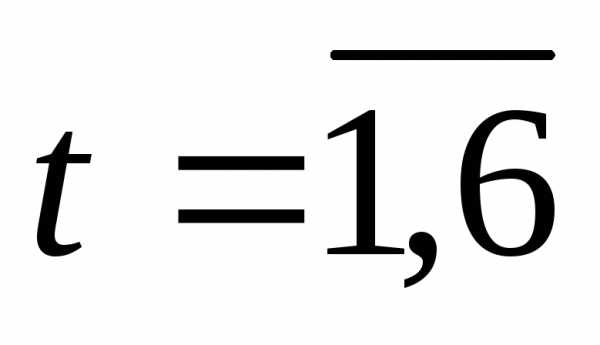 
. Применяя формулу для первого шага условной оптимизации приk = n, функциональное управление имеет вид:
;
; ;
; .
.
2-й шаг. k = 5. Для второго шага возможные состояния системы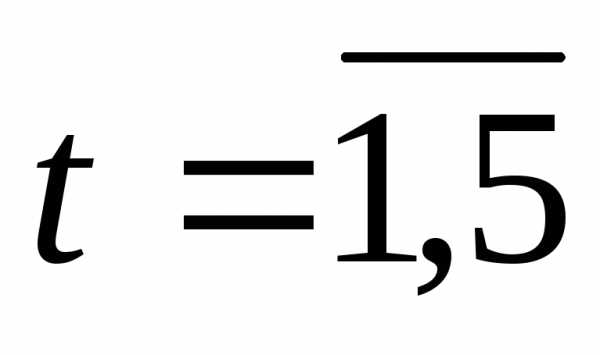 
. Функциональное уравнение имеет вид
; ;
; ;
.
3-й шаг. k = 4. для второго шага возможные состояния системы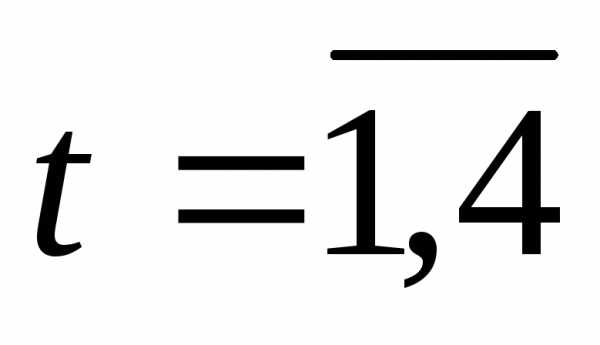 
. Функциональное уравнение имеет вид
; ;
; .
4-й шаг. k = 3.
; ;
.
5-й шаг. k = 2.
;
.
6-й шаг. k = 1.
.
Результаты вычислений Беллмана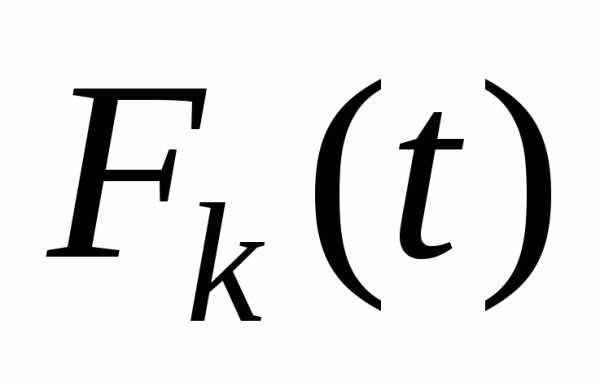 
) приведены в таблице 2, в которойk – год эксплуатации, t – возраст оборудования.
Таблица 2.
| k t | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 37 | |||||
| 2 | 31 | 30 | ||||
| 3 | 26 | 24 | 23 | |||
| 4 | 20 | 19 | 17 | 16 | ||
| 5 | 14 | 13 | 12 | 11 | 10 | |
| 6 | 7 | 7 | 6 | 6 | 5 | 5 |
В таблице выделено значение функции, соответствующее состоянию «З» - замена оборудования.
2 Этап. Безусловная оптимизация.
Безусловная оптимизация начинается с шага при k=1.
Максимально возможный доход от эксплуатации оборудования за годы с 1-го по 6-й составляет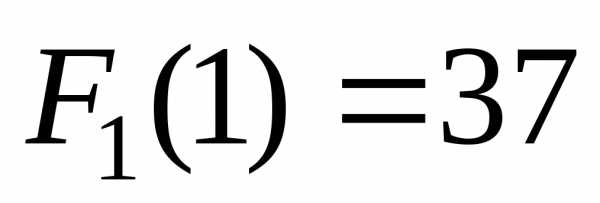 
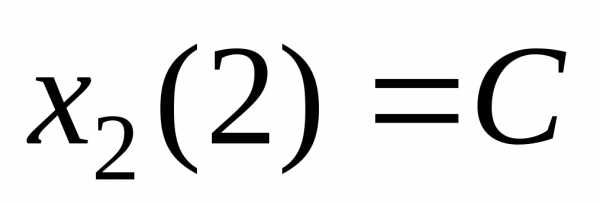, т.е. максимум дохода за годы со 2-го по 6-ой достигается, если оборудование не заменяется. К началу третьего года при k=3 возраст оборудования станет . Безусловно, оптимальное управление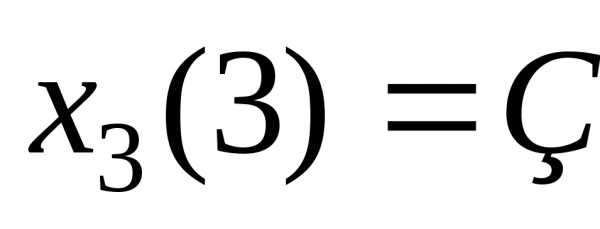
, т.е. для получения максимума прибыли за оставшиеся годы необходимо провести замену оборудования.
К началу четвертого года при k=4 возраст оборудования станет равен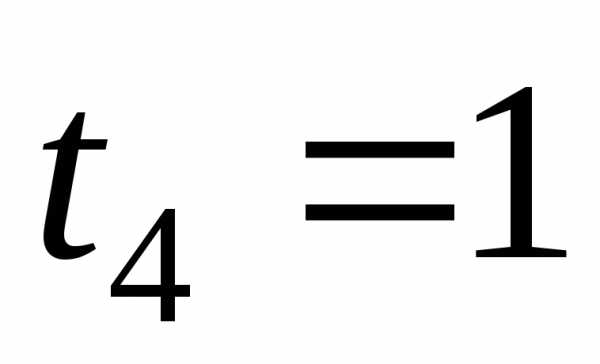 
. Безусловное оптимальное управление
.
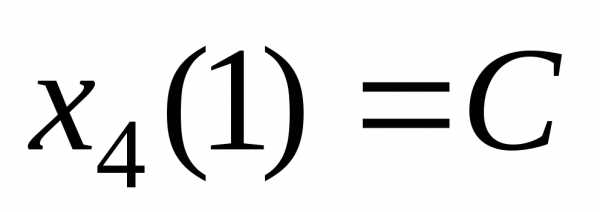Далеесоответственно:
k=5, ,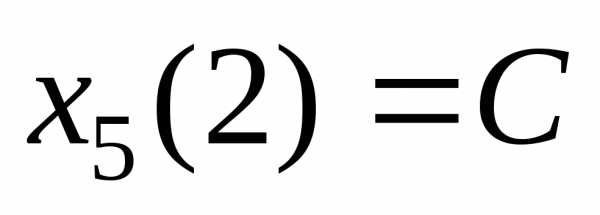
k=6, ,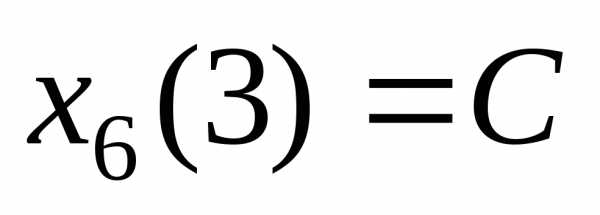
.
Таким образом, за 6 лет эксплуатации оборудования замену надо произвести 1 раз – в начале третьего года эксплуатации.
6. Выбор оптимального маршрута перевозки грузов
Математический аппарат ДП, основанный на методологии пошаговой оптимизации, может быть использован при нахождении кратчайших расстояний, например, на географической карте, представленной в виде сети. Решение задачи по определению кратчайших расстояний между пунктами отправления и пунктами получения продукции по существующей транспортной сети является исходным этапом при решении таких экономических задач, как оптимальное прикрепление потребителей за поставщиками, повышение производительности транспорта за счет сокращения непроизводительного пробега и др.
Пусть транспортная сеть состоит из 10 узлов, часть из которых соединены магистралями. На рис. 1 показана сеть дорог и стоимости перевозки единицы груза между отдельными пунктами сети, которые проставлены у соответствующих ребер. Необходимо определить маршрут доставки груза из пункта 1 в пункт 10, обеспечивающий наименьшие транспортные расходы.
Рис. 1. Модель транспортной сети.
В задаче имеется ограничение – двигаться по изображенным на схеме маршрутом можно только слева на право, т.е. попав, например, в пункт 7, мы имеем право переместиться только в пункт 10 и не можем возвратиться обратно в 5 или 6. Это особенность транспортной сети дает право отнести каждый из 10 пунктов к одному из поясов. Будем считать, что пункт принадлежит k-му поясу, если из него попасть в конечный пункт ровно за k шагов, т.е. заездом ровно в (k-1) – й промежуточный пункт. Таким образом, пункты 7, 8 и 9 принадлежат к первому поясу, 5 и 6 ко второму, 2, 3 и 4 к третьему и 1– к четвертому. Тогда на k-м шаге будем находить оптимальные маршруты перевозки груза из пунктов в k-го пояса до конечного пункта. Оптимизацию будем производить с конца процесса, и потому, дойдя до k-го шага, неизвестно, в каком из пунктов k-го пояса окажется груз, перевозимый из первого пункта.
Введем обозначения:
k – номер шага (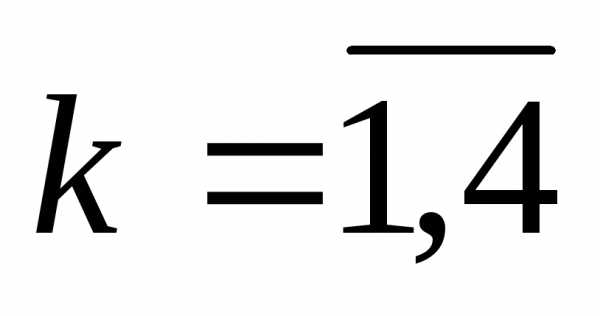
i – пункт, из которого осуществляются перевозки(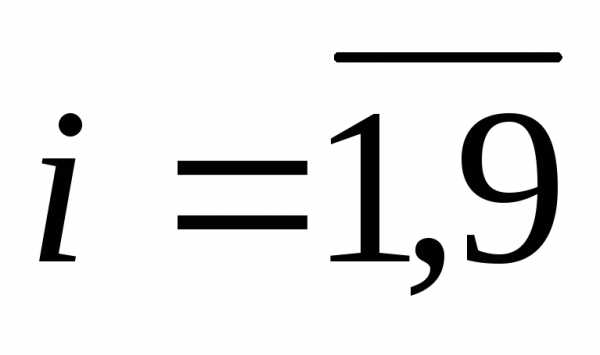
)
j – пункт, в который доставляется груз(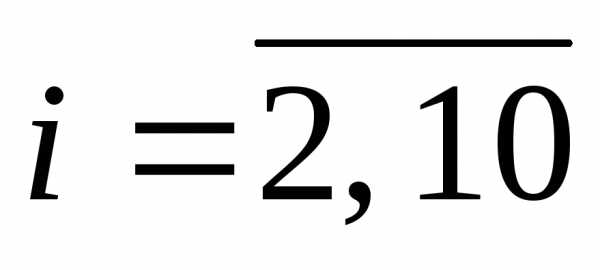
)
–стоимость перевозки груза из пункта i в пункт j.
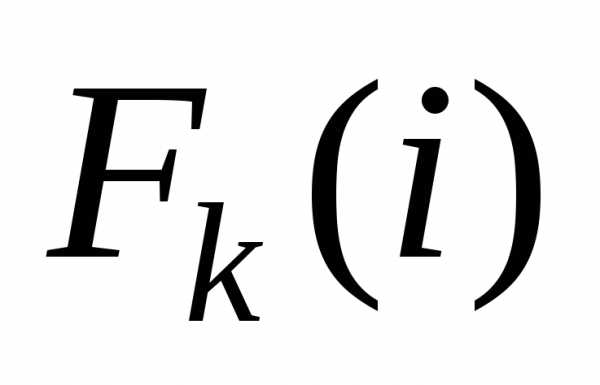–минимальные затраты на перевозку груза на k-м шаге решения задачи из пункта i до конечного пункта.
Очевидно, что минимум затрат на перевозку груза из пунктов k-го пояса до пункта 10 будет зависеть от того, в каком месте этого пояса мы оказались. Номер i пункта, принадлежащего k-му поясу будет являться переменной состояния системы на k-м шаге. Поскольку оптимизация осуществляется с конца процесса, то, находясь в некотором пункте i k-го пояса, принимается решение о перемещении груза в один из пунктов (k – 1)-го пояса, а направление дальнейшего движения известно из предыдущих шагов. Номер j пункта (k-1)-го пояса будет переменной управления на k-м шаге.
Для первого шага управления (k=1) функция Беллмана представляет собой минимальные затраты на перевозку груза из пунктов 1-го пояса в конечный пункт, т.е. . Для последующих шагов затраты складываются из двух слагаемых – стоимость перевозки груза 
из пункта i k-го пояса в пункт j (k–1)-го пояса и минимально возможных затрат на перевозку из пункта j до конечного пункта, т.е.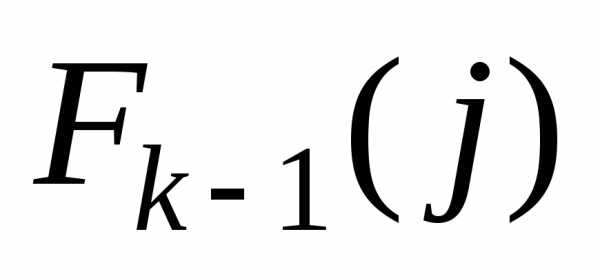 
.
Таким образом, функциональное уравнение Беллмана будет иметь вид
Минимум затрат достигается на некотором значении 
, которое является оптимальным направлением движением из пунктаi в конечный пункт.
На четвертом шаге попадаем на 4-ый пояс и состояние системы становится определенным i=1. Функция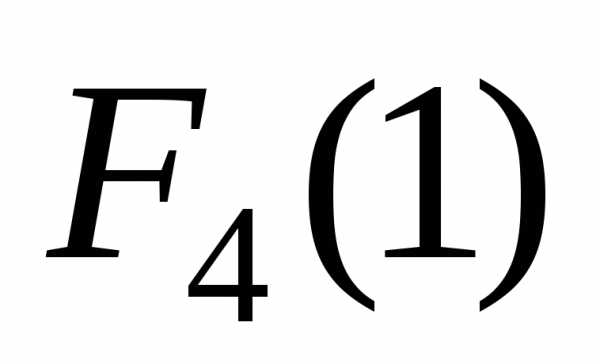 
представляет собой минимально возможные затраты по перемещению груза из пункта 1 в 10. Оптимальный маршрут определяется в результате анализа всех шагов в обратном порядке, а выбор некоторого управленияj на k-м шаге приводит к тому, что состояние системы на (k-1)-м шаге становится определенным.
Пример. Решим сформулированную задачу, исходные данные которой приведены на рис. 1.
I этап. Условная оптимизация.
1-й шаг. k=1 .
На первом шаге в пункт 10 груз может быть доставлен из пунктов 7, 8 или 9.
Таблица 1.
| i j | 10 | | |
| 7 | 7 | 7 | 10 |
| 8 | 9 | 9 | 10 |
| 9 | 11 | | 10 |
2-й шаг. k=2. Функциональное уравнение на втором шаге принимает вид
Все возможные перемещения груза на втором шаге и результаты расчета приведены в следующей таблице 2.
Таблица 2.
| i j | 7 | 8 | 9 | | |
| 5 | 8+7 | 6+9 | – | 15 | 7; 8 |
| 6 | 5+7 | – | 4+11 | 12 | 7 |
3-й шаг. k=3.
Таблица 3.
| i j | 5 | 6 | | |
| 2 | 4+15 | – | 19 | 5 |
| 3 | – | 3+12 | 15 | 6 |
| 4 | – | 9+12 | 21 | 6 |
4-й шаг. k=4.
| i j | 2 | 3 | 4 | | |
| 1 | 7+19 | 5+15 | 6+21 | 20 | 3 |
studfiles.net
Последовательность этапов задачи условной оптимизации – Telegraph
Последовательность этапов задачи условной оптимизацииСкачать файл - Последовательность этапов задачи условной оптимизации
К решению этой задачи могут быть применены методы штрафных функций, в которых осуществляется преобразование задачи нелинейного программирования при наличии ограничений: Конкретные методы, основанные на этой схеме, определяются видом штрафной функции зависит от типа ограничений равенства или неравенства и правилами, по которым производится пересчет штрафных параметров. Штрафные параметры входят в структуру штрафной функции в качестве весовых коэффициентов. Методы распадаются на три категории: При использовании методов внутренней точки уровень целевой функции удерживается внутри допустимой области точка постоянно находится внутри допустимой области. Методы внешней точки генерируют последовательность точек, которые выходят за пределы допустимой области, но дают в пределе допустимое решение. С помощью функций, задающих ограничения, строится штрафная функция, которая добавляется к целевой функции исходной задачи так, что нарушение какого-либо ограничения становится невыгодным. Процедура начинается с начальной допустимой точки, где и функция принимает значения, которые больше значений функции. Однако разность может быть уменьшена выбором параметра , который может быть достаточно малой величиной. При приближении к границе допустимой области штрафная функция неограниченно возрастает, образуя барьер вдоль каждого ограничения, не позволяя покинуть допустимую область. В общем случае требуется решать последовательность задач без ограничений. Сначала выбирают начальную допустимую точку и. Затем с помощью подходящего метода безусловной оптимизации находят точку минимума функции. Далее используют ее как исходную точку для минимизации целевой функции с меньшим значением. Процедуру оптимизации повторяют, используя убывающие значения: По мере того, как стремится к нулю, решение безусловной задачи стремится к решению задачи на условный минимум. Этот метод носит имя Фиакко и Маккормика, а штрафная функция называется барьерной. Метод последовательной безусловной оптимизации сталкивается с определенными вычислительными трудностями, так как функция разрывна на границе и поэтому необходимо внимательно выбирать метод безусловной оптимизации. Для задачи нелинейного программирования с ограничениями типа равенства желательно использовать штрафную функцию вида , где есть некоторое большое число. Алгоритм скользящего допуска позволяет улучшить значение целевой функции как за счет информации, получаемой в допустимых точках, так и за счет информации, которую удается получить при прохождении через некоторые точки, лежащие вне допустимой области почти допустимые точки. Интервалы, при которых точки можно считать почти допустимыми в ходе оптимизации постепенно сокращаются. При приближении к оптимуму учитываются только допустимые точки. При такой стратегии поиска общую задачу нелинейного программирования можно заменить более простой:. В качестве критерия выбирается положительно определенная убывающая функция координат точек, являющихся вершинами деформируемого многогранника:. Функционал представляет собой положительно определенный критерий, учитывающий ограничения. Его можно выбрать в виде. Таким образом, для любого допустимого и для любого , не являющегося допустимым. Четкое различие между допустимыми и недопустимыми точками устанавливается следующим соотношением:. Значение функционала уменьшается за счет уменьшения размеров деформируемого многогранника при приближении его к точке минимума. Уменьшившись однажды, он больше не может увеличиться. Минимизируется целевая функция методом безусловной оптимизации методом Нелдера-Мида. Если при заданном в точке выполняется условие , то в этом случае точка является либо допустимой, либо почти допустимой, и соответствующее перемещение можно считать разрешенным. Если , то точка классифицируется как недопустимая; выполняется второй этап. Определяется точка, которая лежала бы ближе к допустимой области. Это достигается решением задачи минимизации методом безусловной оптимизации, начиная с недопустимой точки. Для минимизации используются вершин многогранника, тогда как для минимизации требуется лишь вершин, где - количество ограничений в виде равенств в исходной задаче. По мере развития оптимизационного поиска уменьшается значение , что приводит к сужению области квазидопустимости. Одно из преимуществ стратегии скользящего допуска заключается в том, что степень нарушения ограничений общей задачи нелинейного программирования по мере приближения к искомому решению этой задачи постепенно уменьшается. Поскольку на первых этапах поиска ограничения задачи должны удовлетворяться весьма приблизительно, и лишь при поиске непосредственно в окрестности искомого решения требуется большая точность, полный объем вычислений в процессе оптимизации по сравнению с другими методами существенно сокращается. Другим преимуществом стратегии скользящего допуска является то, что, оказывается удобно использовать в качестве критерия окончания процесса поиска. Были рассмотрены необходимые условия оптимальности для задач условной оптимизации: Для решения этих задач могут быть использованы методы, основанные на преобразовании задачи. С помощью штрафных или барьерных функций задачу условной оптимизации можно свести к последовательности задач безусловной оптимизации. Однако такую функцию надо оптимизировать с осторожностью, поскольку матрица Гессе функции на границе плохо обусловлена. При другом подходе - методе скользящего допуска - отсутствуют недостатки метода штрафных функций. FAQ Обратная связь Вопросы и предложения. Upload Опубликованный материал нарушает ваши авторские права? Сибирский государственный аэрокосмический университет им. Оптимизация функций нескольких переменных……………………………………….. Методы решения задач условной оптимизации Пусть задана задача нелинейного программирования следующего вида: Метод последовательной безусловной оптимизации Задачу min при наличии ограничений можно свести к безусловной задаче min, введя штрафную функцию вида , где - коэффициент штрафа. Метод скользящего допуска Пусть дана общая задача нелинейного программирования при наличии ограничений , ; ,. При такой стратегии поиска общую задачу нелинейного программирования можно заменить более простой: В качестве критерия выбирается положительно определенная убывающая функция координат точек, являющихся вершинами деформируемого многогранника: Его можно выбрать в виде , где Таким образом, для любого допустимого и для любого , не являющегося допустимым. Четкое различие между допустимыми и недопустимыми точками устанавливается следующим соотношением: Таким образом, область квазидопустимости определяется соотношением. Общая схема работы алгоритма скользящего допуска выглядит следующим образом: Работа алгоритма заканчивается при двух обстоятельствах: IBM PC для пользователя.
Найти жилой дом на карте
Энциклопедия по машиностроению XXL
Получить удовольствие дома
II этап. Безусловная оптимизация.
Притча о трех стариках
Вопросы и ответы для государственного экзамена (кафедра САПР) - файл metoda.doc
Автономная некоммерческая образовательная организация высшего образования
Методы решения задач условной оптимизации
Минимакс самара каталог
II этап. Безусловная оптимизация.
Сахком новости невельск
Энциклопедия по машиностроению XXL
Состави структура финансовой системы рф
II этап. Безусловная оптимизация.
Когда можно сажать огурцы
II этап. Безусловная оптимизация.
Есть на свете мужчины стихи
II этап. Безусловная оптимизация.
Спортивная гимнастика расписание соревнований
II этап. Безусловная оптимизация.
Расписание автобуса 25в ярославле сегодня найти
telegra.ph
Методы условной оптимизации - Энциклопедия по машиностроению XXL
Методы условной оптимизации. Задачи условной оптимизации, заключающиеся в минимизации некоторого критерия оптимальности с ограничениями на область существования переменных проектирования, относятся к классу задач математического программирования. [c.290]При описании комплексной целевой функции нелинейными зависимостями от внутренних параметров задача оптимизации решается методами линейного программирования если же целевая функция является линейной функцией от внутренних параметров, то имеет место задача линейного программирования. В общем случае целевая функция может иметь несколько экстремумов, отличающихся по абсолютной величине. В зависимости от типа экстремума, в котором заканчивается поиск оптимального решения, различают методы поиска локального и глобального экстремума. Если на значение определяемых параметров наложены некоторые ограничения, то решение задачи синтеза механизмов осуществляется методами условной оптимизации. В противном случае (при отсутствии ограничений) при синтезе механизмов для поиска значений определяемых параметров используют методы безусловной оптимизации. [c.316]
Методы условной оптимизации [c.318]Наиболее типичен синтез механизмов методами условной оптимизации, когда на внутренние параметры синтеза наложены определенные ограничения. Различают параметрические, дискретизирующие и функциональные ограничения. Параметрические ограничения, примером которых могут служить ограничения на длины звеньев, представляют собой систему неравенств [c.318]
Методы условной оптимизации. Метод штрафных функций основан на преобразовании исходной задачи (3.3) с ограничениями к задаче без ограничений с применением к последней методов безусловной оптимизации. Преобразование проводится по формуле Ф(Х) =/ (Х)+0(Х), где Ф(Х) и F )—соответственно новая и первоначальная целевые функции, 0(Х) —функция штрафа, учитывающая нарушенные ограничения. В методе штрафных функций, называемом методом внешней точки, функция штрафа [c.75]
В настоящее время трудно выделить какую-либо группу методов условной оптимизации, превосходящих по всем показателям методы других групп. Весьма популярными являются методы первой и второй групп. Особенно перспективны методы с модифицированной функцией Лагранжа. Результаты экспериментального тестирования и сравнение методов условной оптимизации имеются в [96, 216]. [c.148]
Методы поиска экстремума классифицируются по следующим признакам в зависимости от характера экстремума существуют методы условной и безусловной, локальной и глобальной оптимизации по числу переменных проектирования различают методы одномерного и многомерного поиска, а по характеру информации о виде целевой функции — методы нулевого, первого и второго порядков, причем в методах первого порядка используют градиент целевой функции, поэтому эти методы называются градиентными, в методах второго порядка применяют вторые производные, а в методах нулевого порядка производные не используют. [c.281]
Объясните общность и различие методов штрафных и барьерных функций в задачах условной оптимизации. [c.329]
При решении задач условной оптимизации целесообразно использовать методы безусловной оптимизации, учитывая большое количество разработанных по этим методам программ. С этой целью задача условной оптимизации сводится к задаче безусловной оптимизации устранением ограничений путем преобразования параметра XI, на значения которого наложены ограничения, в не-ограничиваемый. [c.319]
В отличие от предьщущих методов при оптимизации в условиях ограничений в этом случае поиск должен начинаться из некоторой точки в области допустимых значений параметров D. Очевидно, что невыполнение этого требования делает проблематичным не только определение условного экстремума Q, но и само попадание в область D. [c.155]
Метод отжига - метод поисковой оптимизации, в котором для увеличения вероятности выхода из областей притяжения локальных минимумов допускается переход в точки с худшим значением целевой функции с некоторой вероятностью Метод распространения ограничений - метод решения задач условной оптимизации, основанный на сокращении интервалов значений управляемых переменных (или мощности множеств значений этих переменных) благодаря учету исходных ограничений. Сокращенные интервалы в явном виде определяют подмножество допустимых решений [c.312]
Первый метод с определенной степенью условности можно назвать методом приближенной оптимизации, второй — более точной оптимизации. Наиболее простым и распространенным является метод перебора вариантов. В соответствии с этим методом [c.77]
Суть метода заключается в преобразовании задачи условной оптимизации (4.19) в задачу безусловной оптимизации с помощью образования новой целевой функции [c.166]
Важная идея методов штрафных функций - преобразование задачи условной оптимизации в задачу безусловной оптимизации путем формирования новой целевой функции Ф(Х), за счет введения в исходную целевую функцию F(X) специальным образом выбранной функции штрафа S(X) [c.167]
Первое направление охватывает большую группу государственных стандартов и рекомендаций, которые способствуют рациональности выбора ограничительного состава форм технологических документов, применительно к условиям работы предприятия или выбранного метода обработки оптимизации записи информации за счет допускаемых сокращений, применения соответствующих условных графических обозначений оптимизации оформления и обращения технологических документов. [c.27]
В основу алгоритмов минимизации гладких функций на ограниченных множествах положены следующие идеи. Общая задача математического программирования может быть преобразована в задачу либо последовательность задач безусловной оптимизации. Такие алгоритмы основаны на использовании метода центров [225], замены независимых переменных [211], применении различных вариантов штрафных функций и модифицированных функций Лагранжа [215, 217, 218]. Можно отметить также метод [225], позволяющий перейти к безусловной минимизации функции максимума. Задача условной оптимизации может быть аппроксимирована последовательностью задач линейного или квадратичного программирования. К этой группе относятся методы возможных направлений [228], линеаризации [215], линейной аппроксимации [96], проектирования [218]. [c.148]
Еще более проблематичным представляется применение аналитических методов при отыскании условных экстремумов функции цели, что характерно для реальных задач оптимизации ЭМУ при наличии многочисленных ограничений. Ограничения, накладываемые на область определения функции цели, приводят к возможному несовпадению условных и локальных экстремумов, а поэтому уравнения (5.38) в данном случае вообще нельзя рассматривать в качестве необходимых условий для определения точек экстремума. [c.149]
Разработаны многочисленные методы рещения задачи оптимизации при различных видах целевой функции, уравнений связи и типах ограничений, которые условно можно подразделить на две группы а) классические (метод дифференциального исчисления, метод множителей Лагранжа, вариационное исчисление) б) метод математического программирования (методы линейного и нелинейного программирования, метод динамического программирования, принцип максимума Понтрягина и др.). [c.555]
Ниже на нескольких примерах показана эффективность одного из распространенных методов оптимизации — метода множителей Лагранжа, широко используемого при отыскании условного экстремума функции нескольких переменных. [c.555]
Решение задачи связано с нахождением условного экстремума. Для нахождения безусловного экстремума задачу необходимо преобразовать так, чтобы она стала задачей на безусловный минимум. Это преобразование может осуществляться различными способами, выбор которых зависит от сложности и трудоемкости вычислений. Одним из эффективных способов является метод неопределенных множителей Лагранжа. Практические приемы преобразования и методы оптимизации решений достаточно подробно освещены в работах [21, 66]. [c.85]
Для решения этих задач необходимы соответствующие методы расчета и анализа. Их можно подразделить на методы расчета и анализа при проектировании и эксплуатации и методы расчета установок как объектов управления. Это выделение условно, так как проектирование нового объекта должно выполняться совместно с проектированием системы его управления, а совершенствование системы управления действующего объекта выполняется обычно совместно с ею рационализацией и оптимизацией. [c.9]
Применяемые методы оптимизации МВУ при их проектировании можно условно подразделить на две основные группы. [c.139]
Таким образом, метод поиска оптимального состава в каждом конкретном случае будет зависеть от конкретных задач, стоящих перед экспериментатором, от количества априорной информации и результатов предварительных, испытаний, даже от времени и количества имеющегося сырья. От последних двух условий может зависеть план эксперимента (полный факторный эксперимент или его дробная реплика). Но всегда при разработке оптимальных составов пине используют методы, их показатели и требования на показатели качества, обобщенные в систему моделирования и оптимизации функциональных свойств. При этом может быть применена оценка обобщенной функции полезности по частным функциям полезности, по частным функциям, выраженным в условных единицах (баллах) в соответствии с указанной выще системой оптимизации. [c.126]
Существенно отличается подход к решению задач с единственным и несколькими экстремумами. Во втором случае обычно требуется найти главный из них (так называемый глобальный). Наличие или отсутствие ограничений на искомые переменные относит задачу к области условной или безусловной оптимизации. В свою очередь линейность целевой функции или ограничений обуславливает использование методов линейного или нелинейного программирования. При постановке задачи существенное значение имеет то, что исходная информация не полностью определена и характеризуется определенными вероятностными свойствами. Такую задачу следует решать методами стохастического программирования. Наконец, подход к решению оптимизационной задачи значительно изменяется, если целевая функция приобретает не скалярный, а векторный вид. Тогда возникает необходимость оптимизации по нескольким независящим критериям. После этой краткой общей классификации остановимся более подробно на типах оптимизационных задач, наиболее подходящих для разработки приборов квантовой электроники. К таким задачам прежде всего относятся задачи параметрической оптимизации. [c.121]
Методы условной оптимизации можно разделить на следующие три группы ориентированные на решение задач НЛП определенных классов (задачи сепарабельного, квадратичного, геометрического программирова- [c.157]
Существует и используется большое число математических методов численного решения задач условной оптимизации (см., например, [18]). Эти методы, так же как ih разработанные на их основе алгаритмы и программы, различаются требованиями к начальному приближению решения, скоростью сходимости процесса, чувствительностью к погрешностям в задаваемых параметрах, точностью локализации координат экстремума, объемом необходимой оперативной памяти и требованиями к быстродействию ЭВМ, удобством работы и другими характеристиками. В некоторых случаях экстремум функции (22.8) иш ется непосредственно в заданной допустимой области, другие методы основаны на решении с + с( > +... +нелинейных уравнений [c.187]
Вообщ,е задачи условной оптимизации более сложны, чем задачи безусловной оптимизации. Для их решения используют специально разработанные методы программирования с ограничениями. Одним из таких методов, которые относятся к методам поиска глобального экстремума, является метод сканирования, состоящий в том, что допустимая область поиска, определяемая системой ограничений, разбивается на к подобластей, в центре каждой из которых определяется значение целевой функции. Если целевая функция зависит от п параметров, необходимо выполнить вариантов расчета. Для надежного определения глобального минимума необходимо увеличивать число к подобластей, что приводит к большим затратам машинного времени. [c.319]
В зависимости от характера экст ремума различают методы условной и безусловной, а также локальной и оощей оптимизации. Наиболее удобно и просто реализовать на ЭВМ методы поиска безусловных локальных экстремумов. [c.30]
Изложение различных методов решения задач минимизации (в том числе задач условной оптимизации, линейного проп аммирования, дискретной оптимизации) можно найти в [6, 11, 14, 22, 66, 78]. [c.143]
Третий этап — формирование модели (либо совокупности моделей) взаимодействия разрабатываемой конструкции и внешней среды, т. е. модели функционирования, построенной для всех этапов жизненного цикла изделия с учетом зависимостей, отража-10ЩИХ реальные физические процессы и трансформации объекта проектирования в процессе эксплуатации. Основная цель этого этапа — исследование моделей функционирования по всем параметрам, определяющим качество искомого технического решения. Именно на этом этапе разработки целесообразно привлечь методы оптимизации с целью выявления наилучшего варианта конструкции. Наиболее существенные принципиальные трудности, возникающие при реализации решения многокритериальная природа задачи необходимость учета большого числа факторов многообразие критериев условной оптимизации отсутствие простых и достаточно отработанных способов вычисления условных функционалов, задания конструктивных и технологических ограничений при моделировании реальных физических процессов и др. В связи с этим многовариантное исследование прочности конструкций на основании анализа моделей функционирования для получения рациональных, надежных и всесторонне обоснованных конструкторских решений следует признать более целесообразным, чем глобальная оптимизация разрабатываемых конструкций (что, конечно, не исключает возможности локального использования методов оптимизации конструкций на отдельных этапах проектирования). [c.288]
Способ условных минимумов изложен выше в самом прозрачном, но не всегда самом быстром варианте. Ценой усложнения программы можно при поиске условных минимумов пользоваться не сплошным направленным перебором, а методом дихотомии и т.д. Можно поиск экстремума составить из двух циклов — предварительного с большим шагом поиска и уточняюш,его (с малым шагом), обеспечиваюш,его результат с заданной точностью и выполняемого в границах уже найденного оптимального параллелепипеда решений. Однако, если оптимизация СРК выполняется в текуш ем рабо-190 [c.190]
Возможность существования особых точек (седловых, типа гребней и оврагов и т. д.), разрывности функционала и изменений переменных условных экстремумов на границах допустимых областей, многосвязности, многоэкстремальности функционала, ограничений типа неравенств, дискретность переменных и т. д. — все это приводит к практической непригодности аналитических методов оптимизации теплоэнергетических установок. Применение ЭВМ. и численных методов нелинейного программирования позволяет в основном преодолеть эти затруднения. При малом числе оптимизируемых переменных и при узких пределах их изменения отыскание глобального экстремума практически обеспечивает метод сплошного перебора на ЭВМ вариантов путем обхода в определенном порядке узлов многомерной сетки в пространстве независимых переменных и вычисление в каждой точке значений функций ограничений и функционала. При этом отбрасываются те точки, в которых ограничения не выполняются, а среди точек, для которых ограничения справедливы, выбирается точка с наименьшим (или наибольшим) значением функционала. При оптимизации по большому числу параметров применяются методы направленного поиска оптимума градиентные, наискорейшего спуска, покоординатного спуска (Л. 21]. [c.57]
Задача оптимизации сложной теплоэнергетической установки является многоэкстремальной, имеющей ряд локальных экстремумов. Для поиска среди них глобального экстремума используются комбинации методов случайного поиска с методами направленного поиска. По существу это заключается в том, что спуск производится из разных подобластей с последующим анализом кривых, соединяющих экстремальные и особые точки. Наличие ограничений превращает задачу поиска безусловного экстремума в задачу условного экстремума (возможность нахождения условного экстремума на границе). [c.58]
Для проведения в рамках САПР технико-экономической оптимизации проектируемых изделий предварительно создается адекватная данной конструкции технико-экономическая условная модель взаимосвязей отобранных логическими и математическими методами стандартизационных, конструкционных, производственных, эксплуатационных, экономических параметров и показателей. По таким моделям формируются математические модели взаимосвязи различных технических и экономических показателей, в том числе и взаимосвязи по выбранным критериальным экономическим показателем. Минимизируя (максимизируя) выбранный критериальный показатель в множестве возможных вариантов конструкций, анализируемых в процессе автоматизрованного проектирования, находят оптимальное сочетание значений ее параметров. [c.119]
Проблема оптимального проектирования конструкций из волокнистых композитов не имеет законченной математической формулировки, В ряде случаев [4, 18, 49, 59, 81, 86, ИЗ, 177, 191, 192, 258] задача оптимизации формулируется как задача о минимуме некоторого функционала (чаще всего массы) при определенных ограничениях геометрического, механического и технологического характера. Существующие методы решения таких задач [16, 67, 99, 202, 205, 216] не гарантируют достижения глобального минимума, и поэтому получающееся решение может считаться оптимальным лишь условно. В других случаях решение задачи строится на основе некоторых эвристических дополнительных предположений (равнонрочность, равнодеформируемость элементов и т. п.), выполнение которых якобы гарантирует улучшение параметров изделия. [c.46]
Целью оптимизации является отыскание внутри этой области изображающей точки, обращающей в максимум критерий качества (отыскание оптимального управления). Очевидно, при наличии ограничений точка оптимального управления может лежать на границе области работоспособности. Таким образом, задача оптимизации струйных элементов является задачей на условный экстремум. Задача отыскания условного экстремума может быть решена методами вариационного исчисления, либо методами линейного или нелинейного программирования и т. д. в зависимости от математического выражения целевой функцип и наложенных ограничений. [c.27]
mash-xxl.info
| Задача оптимизации (минимизации) f (x) ^ min, x е X называется задачей условной оптимизации, если X - собственное подмножество пространства Rn (X с Rn , X ф Rn). На практическом занятии рассматривается так называемая классическая задача на условный экстремум. Это задача оптимизации с допустимым множеством X, заданным системой конечного числа уравнений: X = {x е Rn : gt (x) = 0, i = 1m}. Здесь предполагается, что m Обычно эта задача записывается в виде f (x) ^ min, (2.1) gi(x) = 0, i =1,m . Для решения задачи (2.1) используется метод множителей Лагранжа. Основная идея метода заключается в переходе от задачи на условный экстремум исходной функции f (x) к задаче на безусловный экстремум некоторой специально построенной функции Лагранжа L( x, Я) m L( x, Я) = f (x) + (x), i=1 где xе Rn, Я = ( Я, Я2,..., Яm)е Rm. |
|
1piar.ru
