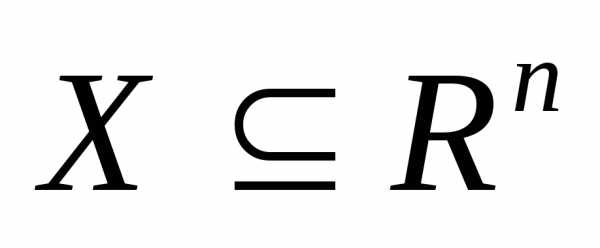ГлавнаяОптимизацияМатематика оптимизация

Оптимизация (математика). Математика оптимизация


Оптимизация (математика) — с русского

См. также в других словарях:

Книги

Другие книги по запросу «Оптимизация (математика)» >>

translate.academic.ru

Оптимизация (математика) - Вики

У этого термина существуют и другие значения, см. Оптимизация.

Оптимизация — в математике, информатике и исследовании операций задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.

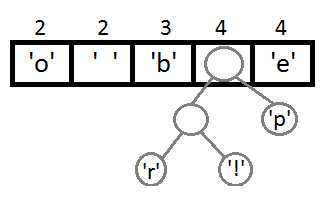
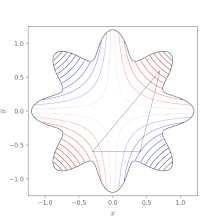Граф параболоида описанного функцией z = f(x, y) = −(x² + y²) + 4. Глобальный максимум от (x, y, z) = (0, 0, 4) обозначен синей точкой Поиск минимума Нелдера-Мида Функции оптимизации. Симплексные вершины упорядочиваются по их значению, при этом 1 имеет наименьшее (лучшее) значение.

Теорию и методы решения задачи оптимизации изучает математическое программирование.

Математическое программирование — это область математики, разрабатывающая теорию, численные методы решения многомерных задач с ограничениями. В отличие от классической математики, математическое программирование занимается математическими методами решения задач нахождения наилучших вариантов из всех возможных.[1]

В процессе проектирования ставится обычно задача определения наилучших, в некотором смысле, структуры или значений параметров объектов. Такая задача называется оптимизационной. Если оптимизация связана с расчётом оптимальных значений параметров при заданной структуре объекта, то она называется параметрической оптимизацией. Задача выбора оптимальной структуры является структурной оптимизацией.

Стандартная математическая задача оптимизации формулируется таким образом. Среди элементов χ, образующих множества Χ, найти такой элемент χ*, который доставляет минимальное значение f(χ*) заданной функции f(χ). Для того, чтобы корректно поставить задачу оптимизации, необходимо задать:

  1. Допустимое множество — множество X={x→|gi(x→)≤0,i=1,…,m}⊂Rn{\displaystyle \mathbb {X} =\{{\vec {x}}|\;g_{i}({\vec {x}})\leq 0,\;i=1,\ldots ,m\}\subset \mathbb {R} ^{n}};
  2. Целевую функцию — отображение f:X→R{\displaystyle f:\;\mathbb {X} \to \mathbb {R} };
  3. Критерий поиска (max или min).

Тогда решить задачу f(x)→minx→∈X{\displaystyle f(x)\to \min _{{\vec {x}}\in \mathrm {X} }} означает одно из:

  1. Показать, что X=∅{\displaystyle \mathbb {X} =\varnothing }.
  2. Показать, что целевая функция f(x→){\displaystyle f({\vec {x}})} не ограничена снизу.
  3. Найти

ru.wikiredia.com

Математическая оптимизация - Энциклопедия по экономике

Критерии и способы оценки сравнительной экономической эффективности проектов детально излагаются в главе 5. Однако вопросы, рассматриваемые на стадии ТЭО, настолько широки и разноплановы, что одних экономических критериев здесь явно недостаточно. Формальные методы математической оптимизации здесь играют подчиненную роль. А главное внимание обращено на творческую проработку ft анализ имеющихся альтернатив. Оценку их эффективности дают с помощью целой группы экономических, социальных, экологических, технико-технологических, а нередко - и международных аспектов. Наиболее удачный вариант проектных решений принимают к осуществлению и утверждают в виде "Технического задания на разработку проекта строительства предприятия" (ТЗ).  [c.55] Математическая оптимизация представляет собой задачу отыскания максимального или минимального значения некоторой целевой функции по заданному параметру (s). Целевая функция есть, таким образом, нечто такое, что может быть оптимизировано только с помощью итеративной процедуры.  [c.172]

Например, отыскание оптимального/для одной рыночной системы или одного сценарного спектра является задачей математической оптимизации. В этих случаях методы математической оптимизации могут быть достаточно грубыми, вроде перебора всех значений / от 0 до 1,0 с шагом 0,01. В качестве целевой функции для отыскания среднего геометрического HPR при различных условиях и заданном значении/может выступать одна из функций, представленных в главе 1. Роль варьируемого параметра здесь играет то значение / которое тестируется в интервале от 0 до 1.  [c.172]

Теперь, когда у нас есть координаты для отдельной точки (ее широта, долгота и высота), нам нужна некая процедура поиска, метод математической оптимизации, для изменения значений / подставляемых в целевую функцию таким образом, чтобы возможно скорее и проще добраться до вершины поверхности.  [c.173]

В прошлом было разработано множество методов математической оптимизации, многие из которых весьма продуманны и эффективны. У нас есть из чего выбирать. Ключевым вопросом является К какой целевой функции мы будем применять эти методы математической оптимизации в нашей новой методологии инвестирования капитала Целевая функция является ее сердцевиной. Далее мы обсудим этот вопрос и проиллюстрируем на примерах, как работать с целевыми функциями. После этого мы займемся методами оптимизации целевых функций.  [c.173]

Далее, руководствуясь используемым методом математической оптимизации, мы стали бы изменять наши значения/ В итоге мы нашли бы оптимальные значения 0,21, 0,21, 0,21 для / , f2 и fv соответственно. Это дало бы нам  [c.181]

Это среднее геометрическое HPR дает нам высоту в (п + 1)-мерном пространстве. Нам нужно найти вершину в этом пространстве, поэтому далее нам следует выбрать и опробовать новый набор значений /, который помог бы нам найти эту вершину. Этот процесс и называется математической оптимизацией.  [c.182]

Математическая оптимизация или отыскание корней  [c.183]

Можно сказать, что отыскание корней имеет отношение к математической оптимизации, так как первая производная в точке оптимума функции (т. е. на экстремуме) будет равна 0. Следовательно, вы могли бы заключить, что традиционные методы отыскания корней, например метод Ньютона, можно использовать для решения оптимизационных задач (применение собственно методов оптимизации для отыскания корней уравнения, напротив, чревато обилием трудностей).  [c.183]

Кроме двух описанных грубых методов математической оптимизации существуют и более совершенные. Это — замечательная ветвь современной математики, и я настоятельно призываю вас познакомиться с ней, просто в надежде, что вы извлечете из этого какую-то долю того удовлетворения, которую получил я от ее изучения.  [c.185]

В целом, различные методы математической оптимизации могут быть классифицированы по принципу используемого аппарата следующим образом  [c.186]

Хотя вы можете использовать любой упомянутый алгоритм многомерной оптимизации, я предпочел генетический алгоритм потому, что он является, возможно, единственным наиболее устойчивым методом математической оптимизации, за исключением весьма грубых приемов перебора всех возможных комбинаций значений переменных.  [c.188]

Методы математической оптимизации, 623  [c.768]

Наиболее важным и перспективным и в то же время наименее разработанным является применение методов математической оптимизации в народнохозяйственном планировании.  [c.93]

Методы оптимизации означают попытку установить оптимальный уровень цен с использованием аналитической зависимости или просто в числовом виде. В общих чертах установление оптимальных цен включает (1) описание и оценку функций спроса и затрат (последние работы также включают функции конкурентной реакции в оптимизационном подходе) (2) выбор целей ценообразования (в большинстве случаев максимизация прибыли) (3) назначение оптимальных цен с использованием методики математической оптимизации.  [c.521]

Как и оптимизационное ценообразование, имитационные методы в первую очередь уточняют и оценивают соотношение спроса и цены, после чего выбираются цели ценообразования и в конце определяется цена, которая наилучшим образом отвечает данным целям. Оба метода различаются, однако, тем, как устанавливаются оптимальные цены. Поскольку методы оптимизации используют технику математической оптимизации для исчисления оптимальной цены, методы имитации оценивают и сравнивают результаты различных сценариев ценообразования. Тот сценарий, который дает лучшие результаты, обеспечивает почти оптимальные цены.  [c.522]

Экономико-математическое моделирование является важным инструментом планового управления. Различаются группы моделей графические, корреляционные (регрессионные), балансовые, модели оптимизации экономики.  [c.72]

Модели оптимизации экономики имеют целью добиться наибольшей результативности (эффективности) использования имеющегося потенциала и ресурсов. Любая экономико-математическая модель — это воспроизведение связей между экономическими явлениями и процессами. Критерии оптимального плана могут быть разными, поэтому в общей форме подразумевается оптимальное сочетание цели и средств социалистического производства за счет интенсивного использования всех имеющихся возможностей. Целевая функция и ограничения выражаются в математическом виде, и решение их методами линейного программирования позволяет найти оптимальный вариант.  [c.73]

В системе оперативно-производственного планирования важную роль играют расчеты наиболее рациональной загрузки производственного оборудования и производственных площадей. Имеется в ниду не только сопоставление планируемого объема работ на квартал, месяц с производственной мощностью оборудования и размерами производственных площадей, но и оптимизация распределения годового задания по периодам года, а также оптимизация закрепления номенклатуры продукции за оборудованием. Эти расчеты выполняются по группам взаимозаменяемого оборудования. Очень часто на предприятиях решается только первая часть задачи — проверка соответствия оперативного задания мощности цеха. Другая, наиболее интересная задача — обоснование наилучшей загрузки оборудования — требует многовариантных расчетов, и ее без использования вычислительной техники трудно осуществить. Порядок экономико-математического моделирования задач подобного типа и методы решения их рассмотрены в гл. IX.  [c.197]

Эта система позволяет за счет интеграции отдельных расчетов повысить комплексность разрабатываемых плановых рекомендаций. Объемы производства, направления распределения продукции, трудовых и финансовых ресурсов, показатели себестоимости, рентабельности, производительности труда др. должны определяться в одном цикле на основе отраслевых взаимосвязанных моделей. Благодаря использованию быстродействующих средств вычислительной техники резко увеличивается число вариантов плановых расчетов и обеспечивается возможность сократить сроки разработки народнохозяйственных планов и быстрее доводить их до предприятий. Применение экономико-математических методов оптимизации позволяет принимать наилучшие варианты плановых решений. Создается возможность рационально перераспределять ресурсы при изменении целей, задач и условий развития экономики в целом и отдельных ее звеньев.  [c.118]

Для оптимизации производственной программы разработан ряд статических экономико-математических моделей, основанных на методах линейного программирования и с достаточной точностью описывающих возможности нефтеперерабатывающего предприятия. Критериями оптимальности служат максимум прибыли, минимум затрат, максимум выработки товарной про-  [c.162]

Совершенствование организационной структуры управления нефтеперерабатывающими предприятиями возможно путем укрупнения цехов и участков, централизации и специализации работ, концентрации функций управления вспомогательными службами, оптимизации численности инженерно-технических работников и служащих, широкого применения экономико-математических методов, электронно-вычислительной техники, организационной техники н средств связи. Необходим системны подход к проектированию структур управления.  [c.328]

Модуль II. Моделирование управленческих решений и их оптимизация (Математические методы принятия решений).  [c.452]

Оптимизация использования рабочего времени персонала Математическое программирование Математическая статистика  [c.159]

Поэтому особое значение приобретают вопросы подготовки производства, организации технического контроля, научной организации труда и управления, оптимизации плана, обеспечения достоверной систематической, надежной информацией для оперативного планирования и управления производством с использованием экономико-математических методов (ЭММ) и электронно-вычислительных машин (ЭВМ).  [c.12]

Использование современных математических методов и ЭВМ для нахождения оптимального варианта трудового процесса открывает широкие перспективы совершенствования организации и нормирования труда, заложенные в оптимизации трудовых процессов.  [c.165]

В химических производствах используется оборудование незаменяемое и взаимозаменяемое. Для оптимизации использования оборудования применяются экономико-математические модели.  [c.245]

Термины оптимизация и оптимальный ассоциируются с экономико-математическими методами (ЭММ) и ЭВМ, т. е. с методами и средствами, способствующими наиболее эффективному решению задач планирования и управления. Вместе с тем и в действующей практике, основанной на традиционных методах, руководитель любого уровня управления на предприятии также заинтересован в оптимальном решении вопроса по увеличению выпуска продукции, снижению затрат на производство, использованию капиталовложений и т. Д. Но он пытается этого достичь, пользуясь в основном установившимися принципами общих закономерностей и далеко не совершенными вычислительными средствами. При этом во многих случаях также рассматривается ряд вариантов, хотя и ограниченный, что обусловливается реальными организационными и техническими возможностями. Тем не менее в отдельных случаях не исключено совпадение результатов решения, полученных с использованием ЭММ и ЭВМ и на основе традиционного подхода.  [c.377]

В подтверждение достаточной сложности математической формализации ряда оптимизационных задач ниже приведена линейная модель для расчета производственной программы предприятия . Подобного рода модель оптимизации текущего заводского планирования характерна для предприятий химической, нефтехимической и нефтеперерабатывающей промышленности, имеющих принципиальное сходство в построении технологических процессов (для непрерывных производств).  [c.407]

Формализация критерия предусматривает математическую запись основного показателя, например прибыли предприятия, исходя из оптимизации которого следует устанавливать плановые задания отдельным технологическим участкам (установкам, цехам) на данный плановый период (год, квартал, месяц).  [c.408]

Таким образом, при построении экономико-математической модели, предназначенной для оптимизации производственной программы всего предприятия, должны быть прежде всего учтены реальные производственные возможности и интересы отдельных технологических участков, ресурсы и интересы всего предприятия, а также плановые лимиты по сырью и готовой продукции.  [c.408]

Не существует ни одного допустимого плана. Математически это означает, что модель — система уравнений и неравенств — противоречива, что нельзя подобрать такие числовые значения неизвестных, при которых выполнялись бы одновременно все уравнения и неравенства. Технологически это, как правило, означает, что в данном плановом периоде из данных объемов сырья при данных производственных мощностях нельзя произвести товарную продукцию в данном ассортименте и количестве. Естественно, что об оптимизации здесь говорить не приходится. Однако если такой случай встретился, то обсуждаемая нами задача расчета производственной программы вскроет конкретно невыполнимые требования и укажет пути их устранения или посредством снижения этих требований, или увеличением ресурсов, выделяемых предприятию.  [c.414]

Оптимизация планов работы предприятия имеет важное значение. Суть автоматизированного управления заключается в планировании работы предприятия, определении фактического исполнения плана, принятии управляющих воздействий, направленных на реализацию общих для предприятия плановых заданий. При этом планирование работы предприятия осуществляется периодически. Рассмотрим пример построения модели, учитывая важность функции планирования в АСУП и то, что оптимизация планов осуществляется с помощью экономико-математической модели.  [c.415]

В отрасли выполнены и внедрены в практику экономико-математические модели оптимизации и размещения производства асинхронных низковольтных электродвигателей, силовых трансформаторов, кабельной техники, источников света и светотехнических изделий, электрокерамических изделий, объем производства которых составляет около 40% отраслевого выпуска. За основу принимались динамические производственно-транспортные модели в вариантной постановке с дискретными переменными. Вместе с тем в каждом конкретном случае учитывалась специфика электротехнических производств.  [c.27]

Для использования в планировании ЭММ необходимы экономико-математические модели, содержащие основные параметры процессов и выражающие их связи в виде уравнений или неравенств. В электротехнической промышленности накоплен значительный опыт оптимизации планирования. В наибольшей мере это относится к решению задачи перспективного планирования, развития, специализации и размещения отрасли и отдельных производств. Оптимизация планирования в отрасли позволяет учитывать в расчетах значительно большее число факторов, чем при использовании традиционных методов планирования, выбирать наилучший из вариантов в заданных условиях с точки зрения критерия оптимальности. За основу принимаются динамические производственные или производственно-транспортные модели в вариантной постановке с дискретными переменными. Вместе с тем в каждом конкретном случае учитывается специфика производства.  [c.78]

Ранжировать территории по обобщающему показа гелю состояния окружающей среды, выбрать вариант, оптимальный с точки зрения многих критериев, по мнению автора, целесообразно посредством использования аппарата векторной оптимизации и теории нечетких множеств. Оригинальный подход был разработан на кафедре математического моделирования Уфимского государственного нефтяного технического университета и  [c.4]

Математическую оптимизацию можно вкратце описать следующим образом. У вас есть некая целевая функция (обозначим ее G), зависящая от одного или большего количества независи-  [c.183]

Основной недостаток алгоритма — это большой объем накладных расходов на обработку данных, требуемых для расчета и хранения вариантов решений. Тем не менее, благодаря своей конструктивной устойчивости и эффективности приложений в области оптимизационных проблем, будь то крупные, нелинейные или зашумленные, по убеждению автора, он станет фактически предпочтительным методом оптимизации в будущем (не считая появления лучших алгоритмов, обладающих теми же желательными свойствами). По мере того, как компьютеры становятся все более мощными и дешевыми, проблема вычислительных издержек утрачивает свою остроту. Воистину, если бы скорость обработки была нулевой, если бы скорость не играла роли, то генетический алгоритм стал бы предпочтительным методом решения для почти всех задач математической оптимизации.  [c.191]

АСУнефтеснаб рассматривается прежде всего как экономическая система, целью разработки и внедрения которой является совершенствование управления процессом обращения нефтепродуктов в народном хозяйстве в результате качественного изменения характера, содержания и функций управленческого труда оптимизации различных сторон производственно-хозяйственной деятельности организаций системы нефтеснабжения, повышения оперативности управления отдельными звеньями и объектами системы нефтеснабжения широкого использования экономико-математических и других современных методов в управлении нефтеснабжением устранения параллелизма и дублирования при выполнении управленческих работ унифицирования и значительного сокращения документации, сведения ее к ограниченному числу форм и таблиц обеспечения рациональных потоков и повышения коэффициента использования экономической информации.  [c.329]

АСУТПбурения предусматривает применение экономико-математических методов, информационных и электронно-вычислительных систем. При этом предусматривается оптимизация основных технологических процессов механического бурения, спуско-подъемных операций, вскрытия продуктивных горизонтов, их опробования и испытания, спуска обсадных колонн и цементирования.  [c.86]

В последние годы уровень автоматизации процессов в нефтепереработке и нефтехимии значительно возрос. Разработаны и внедрены анализаторы качества продукции в потоке, уровнемеры, индикаторы составов, хроматографы, газоанализаторы, на многих предприятиях функционируют товарные парки с полной автоматизацией замера уровня и дистанционным управлением переключения, автоматизированы слив и налив сырья и продукции, разработаны и внедрены локальные системы автоматического регулирования различного назначения (системы автоматизации переключения контактных печей с контактирования на регенерацию, автоматического регулирования состава углеводородной шихты, оптимизации процессов дегидрирования бутана в бутилен и бутилена в бутадиен, автоматического управления процессом эмульсационной полимеризации и др.). На технологических установках (каталитического рифор-минга, пиролиза, полимеризации) внедряют управляющие вычислительные машины (УВМ). Внедрение УВМ знаменует переход к более высокому уровню автоматизации и обеспечивает дальнейший рост эффективности производства. Так, применение на одном из предприятий УВМ УМ-1 для оперативного управления и контроля процесса гидроочистки дизельного топлива дало 170 тыс. руб. годовой экономии. Использование экономико-математических методов и УВМ для компаундирования товарной продукции обеспечило 7 млн. руб. экономии. Коми-  [c.109]

economy-ru.info

Prostoy-Site | Все права защищены © 2018 | Карта сайта