2.1. Градиентные методы. Градиентный метод оптимизации

2.1. Градиентные методы

Градиентные методы поиска оптимума целевой функции основаны на использовании двух основных свойств градиента функции.

1. Градиент функции 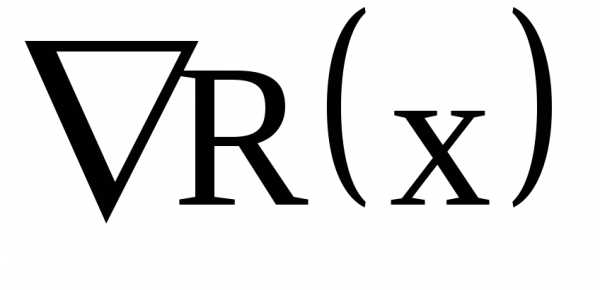– это вектор, который в каждой точке области определения функции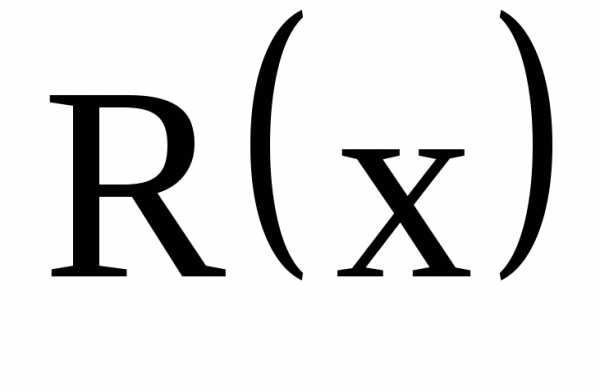направлен по нормали к поверхности уровня, проведенной через эту точку.

Проекции градиента 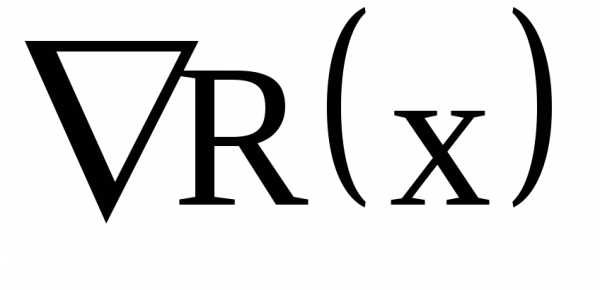на оси координат равны частным производным функции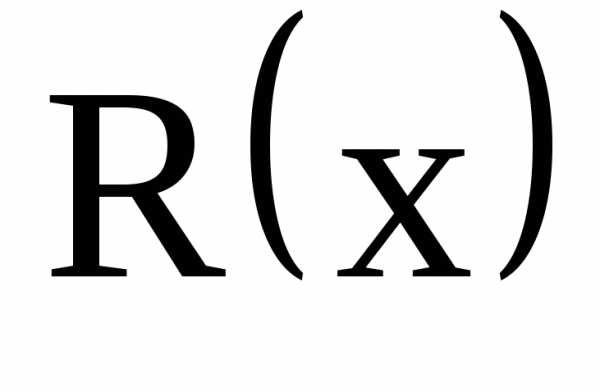по соответствующим переменным, т.е.

. (2.4)

2. Направление градиента характеризует направление наибольшего возрастания функции.

К градиентным методам относятся: метод релаксации, градиента, наискорейшего спуска и ряд других [1,2,5].

Рассмотрим некоторые из градиентных методов.

Метод градиента

В этом методе спуск производится в направлении наибыстрейшего изменения целевой функции, что, естественно, ускоряет процесс поиска оптимума.

Поиск оптимума производится в два этапа. На первом этапе находятся значения частных производных по всем независимым переменным, которые определяют направление градиента в рассматриваемой точке. На втором этапе осуществляется шаг в направлении, обратном направлению градиента (при поиске минимума целевой функции).

При выполнении шага одновременно изменяются значения всех независимых переменных. Каждая из них получает приращение пропорциональное соответствующей составляющей градиента по данной оси.

Формульная запись алгоритма может иметь вид:

,. (2.5)

В этом случае величина шага 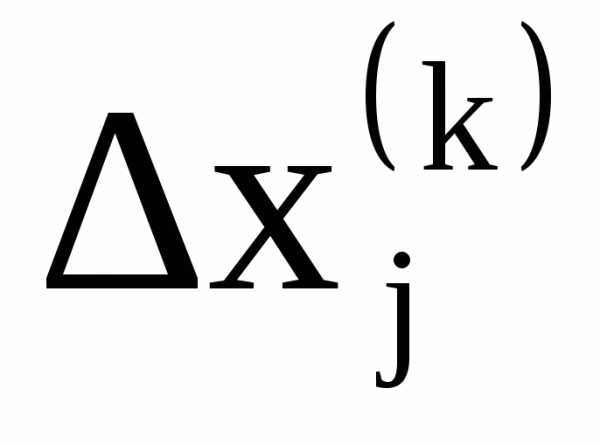при постоянном значении параметраhизменяется автоматически с изменением величины градиента и при приближении к оптимуму уменьшается.

Другая формульная запись алгоритма имеет вид:

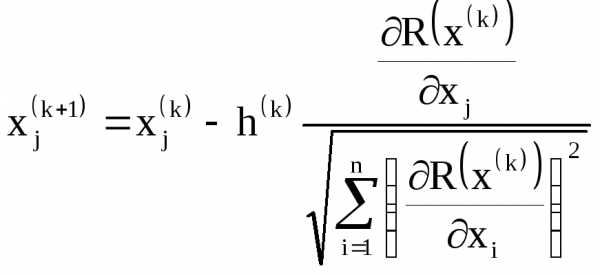,. (2.6)

В этом алгоритме используется нормализованный вектор градиента, указывающий лишь направление наискорейшего изменения целевой функции, но не указывает скорости изменения по этому направлению.

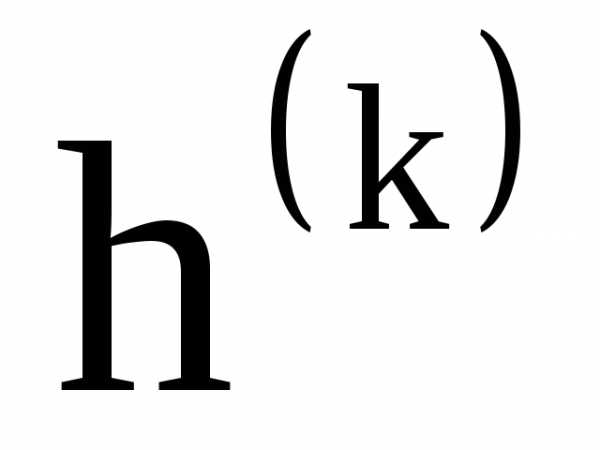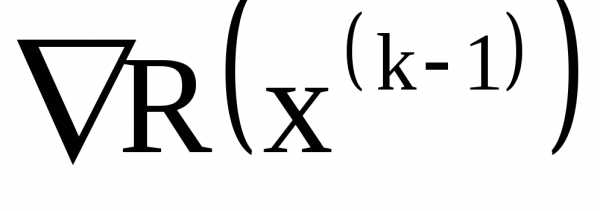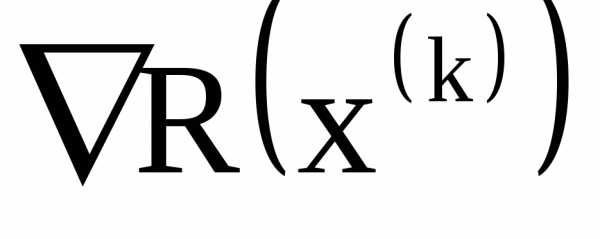В стратегии изменения шага в этом случае используется то, что градиенты и отличаются по направлению. Изменение шага поиска производится в соответствии с правилом:

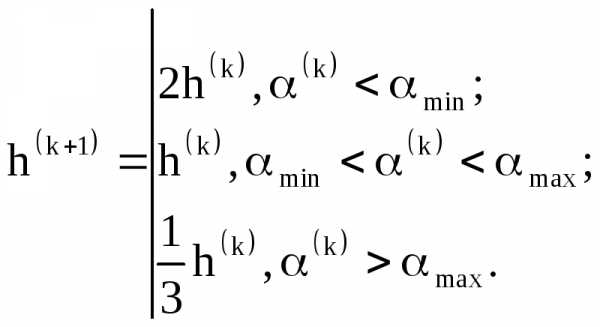(2.7)

где 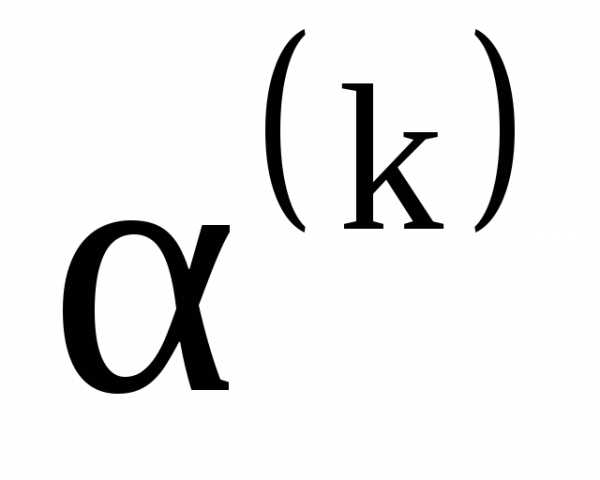– угол поворота градиента наk-ом шаге, определяемый выражением

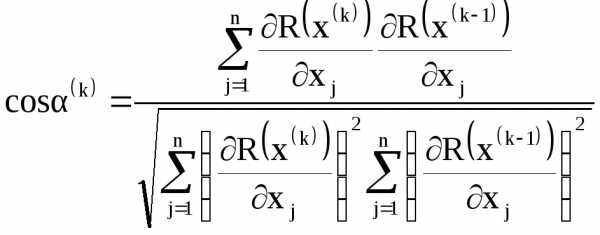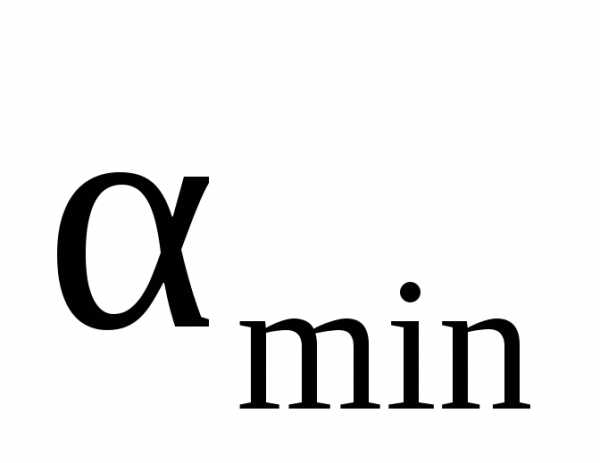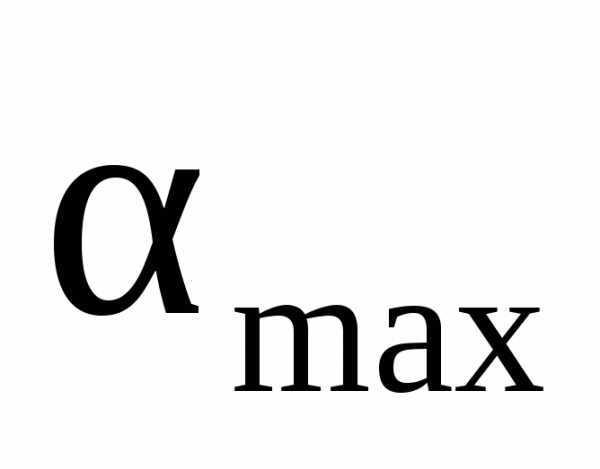,– допустимые пределы угла поворота градиента.

Характер поиска оптимума в методе градиента показан на рис. 2.1.

Момент окончания поиска можно найти проверкой на каждом шаге соотношения

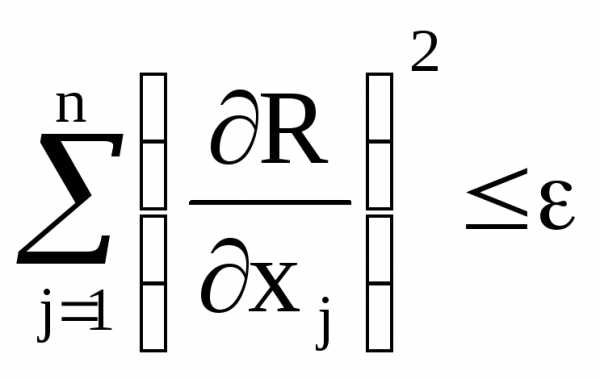где – заданная погрешность расчета.

Рис. 2.1. Характер движения к оптимуму в методе градиента с большой величиной шага

Недостатком градиентного метода является то, что при его использовании можно обнаружить только локальный минимум целевой функции. Для того, чтобы найти у функции другие локальные минимумы, необходимо производить поиск из других начальных точек.

Другим недостатком этого метода является значительный объем вычислений, т.к. на каждом шаге определяются значения всех частных производных оптимизируемой функции по всем независимым переменным.

Метод наискорейшего спуска

При применении метода градиента на каждом шаге нужно определять значения частных производных оптимизируемой функции по всем независимым переменным. Если число независимых переменных значительно, тогда объем вычислений существенно возрастает и время поиска оптимума увеличивается.

Сокращения объема вычислений можно добиться используя метод наискорейшего спуска.

Сущность метода заключается в следующем. После того как в начальной точке будет найден градиент оптимизируемой функции и тем самым определено направление ее наибыстрейшего убывания в указанной точке, в данном направлении делается шаг спуска (рис. 2.2).

Если значение функции в результате этого шага уменьшилось, производится очередной шаг в том же направлении, и так до тех пор, пока в этом направлении не будет найден минимум, после чего вычисляется градиент и определяется новое направление наибыстрейшего убывания целевой функции.

Рис. 2.2. Характер движения к оптимуму в методе наискорейшего спуска ( – ) и методе градиента (∙∙∙∙)

В сравнении с методом градиента метод наискорейшего спуска оказывается более выгодным из-за сокращения объема вычислений.

Важной особенностью метода наискорейшего спуска является то, что при его применении каждое новое направлении движения к оптимуму ортогонально предшествующему. Это объясняется тем, что движение в одном направлении производится до тех пор, пока направление движения не окажется касательным к какой-либо линии постоянного уровня.

В качестве критерия окончания поиска может использоваться то же условие, что и в рассмотренном выше методе.

Кроме того, можно также принять условие окончания поиска в форме соотношения

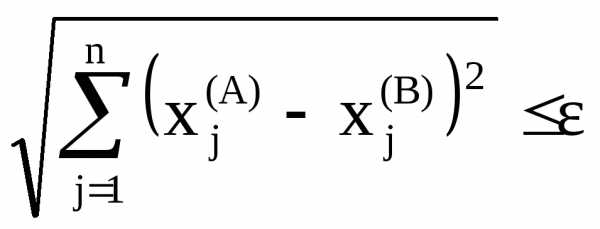где 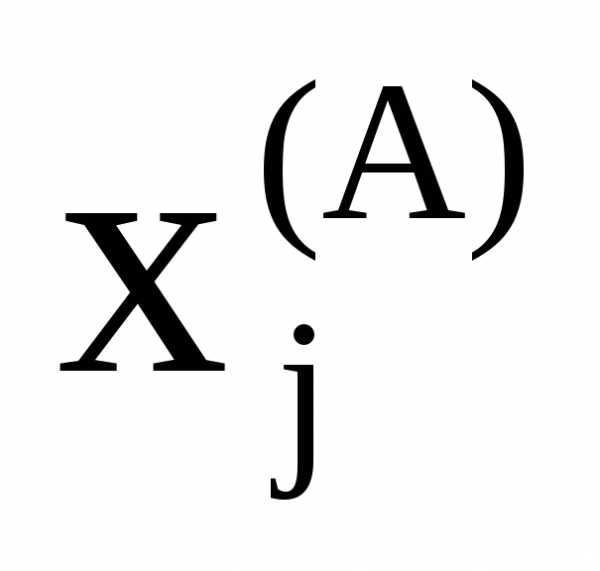и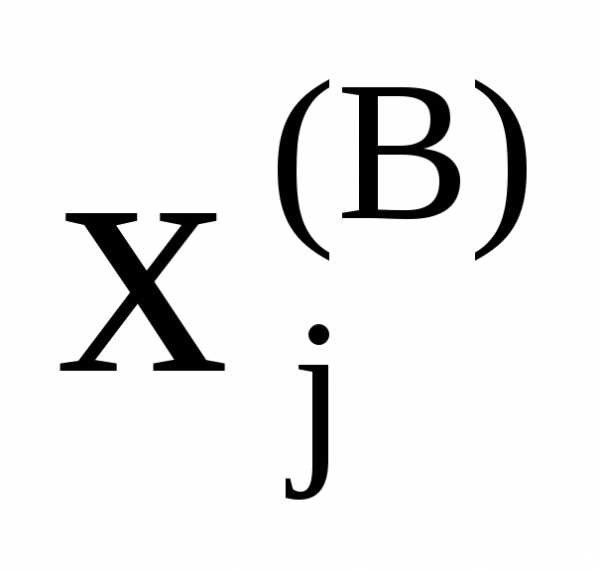–координаты начальной и конечной точек последнего отрезка спуска. Этот же критерий может использоваться в сочетании с контролем значений целевой функции в точках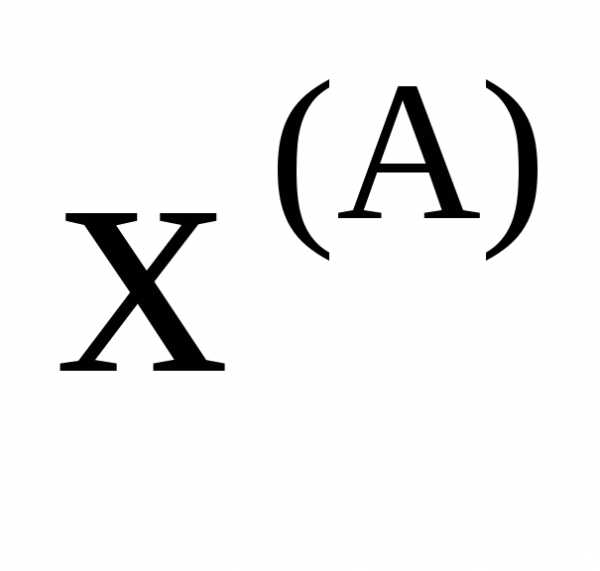и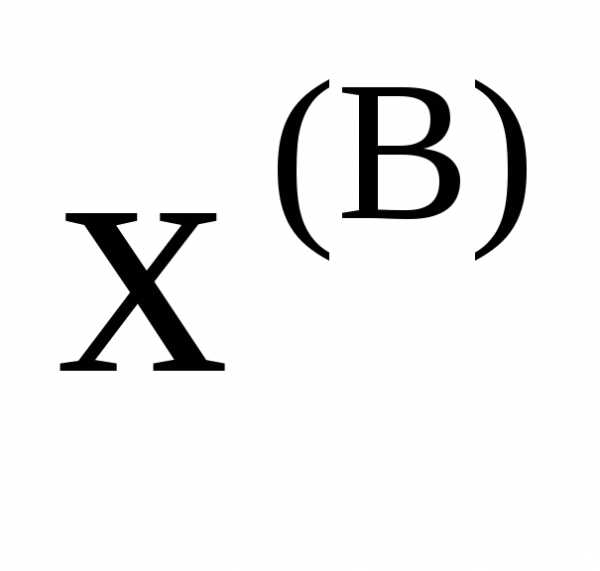

Совместное применение условий окончания поиска оправдано в тех случаях, когда оптимизируемая функция имеет резко выраженный минимум.

Рис. 2.3. К определению окончания поиска в методе наискорейшего спуска

В качестве стратегии изменения шага спуска можно использовать методы изложенные выше (2.7).

studfiles.net

Метод градиента - это... Что такое Метод градиента?

Метод градиента

Градиентный спуск — метод нахождения локального минимума (максимума) функции с помощью движения вдоль градиента. Для минимизации функции в направлении градиента используются методы одномерной оптимизации, например, метод золотого сечения. Также можно искать не наилучшую точку в направлении градиента, а какую-либо лучше текущей.

Сходимость метода градиентного спуска зависит от отношения максимального и минимального собственных чисел матрицы Гессе в окрестности минимума (максимума). Чем больше это отношение, тем хуже сходимость метода.

Описание

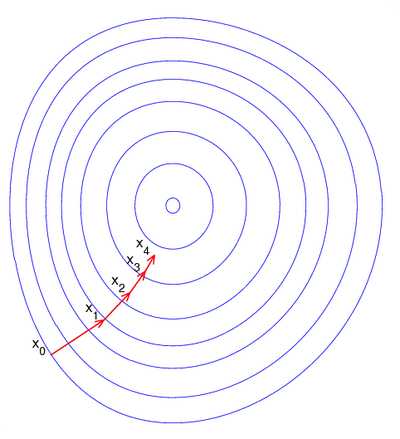
Иллюстрация последовательных приближений к точке экстремума в направлении наискорейшего спуска (красн.) в случае дробного шага. Синим отмечены линии уровня.

Пусть целевая функция имеет вид:

И задача оптимизации задана следующим образом:

Основная идея метода заключается в том, чтобы идти в направлении наискорейшего спуска, а это направление задаётся антиградиентом :

где λ[j] выбирается

постоянной, в этом случае метод может расходиться;
дробным шагом, т.е. длина шага в процессе спуска делится на некое число;
наискорейшим спуском:

Алгоритм

Задают начальное приближение и точность расчёта
Рассчитывают , где
Проверяют условие остановки:
- Если , то j = j + 1 и переход к шагу 2.
- Иначе и останов.

Пример

Применим градиентный метод к функции . Тогда последовательные приближения будут выглядеть так:

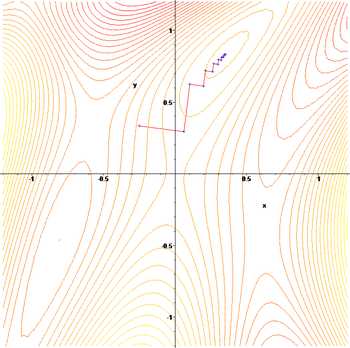
Упомянем, что метод наискорейшего спуска может иметь трудности в патологических случаях овражных функций, так, к примеру, в случае функции Розенброка.

Пример реализации

C++

#include <vector> #include <iostream> #include <Math.h> #include <string> #include <sstream> #include <TCHAR.h> using namespace std; typedef vector<double> DataList; void InitData(); void GradSearch(DataList &p, double sigma,double epsilon); void QMin(DataList &de_dxi, DataList &p, double epsilon, double sigma); void getDfDx(DataList &de_dxi, DataList &p); string CreateResultString(DataList &pMin,double yMin); double getFunc(DataList &p); string stringify(double x); DataList p1; DataList p2; DataList pMin; DataList de_dxi; double yMin; double err; double z0; double h; int N; int j; int main(int argc, _TCHAR* argv[]) { N = 2; InitData(); DataList p; p.push_back(0.99); p.push_back(1.01); double sigma = 0.0000000001; double epsilon = 0.0000000001; GradSearch(p, sigma, epsilon); return 0; } void GradSearch(DataList &p, double sigma,double epsilon) { int max = 60; h = 1; err = 1; int count = 0; while(count < max && (h>sigma ||err > epsilon)) { getDfDx(de_dxi, p); QMin(de_dxi, p, epsilon, sigma); for(int i = 0; i<N; i++) p.at(i) = pMin.at(i); z0 = yMin; count = count + j + 1; string iterResult = CreateResultString(pMin, yMin); cout<<CreateResultString(pMin, yMin)<<endl; } cout<<endl<<"Минимум функции: "<<"-4*x + x*x - y - x*y + y*y"<<endl; cout<<CreateResultString(pMin, yMin)<<endl; } void QMin(DataList &de_dxi,DataList &p, double epsilon, double sigma) { int cond = 0; int jmax = 60; z0 = getFunc(p); for(int i = 0; i<N; i++) p1.at(i) = p.at(i) + h * de_dxi.at(i); double y1 = getFunc(p1); for(int i = 0; i<N; i++) p2.at(i) = p.at(i) + 2 * h * de_dxi.at(i); double y2 = getFunc(p2); j = 0; while (j<jmax && cond == 0) { if (z0<=y1) { for(int i = 0; i<N; i++) p2.at(i) = p1.at(i); y2 = y1; h = h / 2; for(int i = 0; i<N; i++) p1.at(i) = p.at(i) + h * de_dxi.at(i); y1 = getFunc(p1); } else if (y2 < y1) { for(int i = 0; i<N; i++) p1.at(i) = p2.at(i); y1 = y2; h = h*2; for(int i = 0; i<N; i++) p2.at(i) = p.at(i) + 2 * h * de_dxi.at(i); y2 = getFunc(p2); } else { cond = -1; } j = j+1; if (h < sigma) cond = 1; } double hMin = (h/2)* (4 * y1 - 3* z0 - y2) / (2* y1 - z0 - y2); for (int i = 0; i< N; i++) { pMin.at(i) = p.at(i) + hMin * de_dxi.at(i); } yMin = getFunc(pMin); double h0 = fabs(hMin); double h2 = fabs(hMin - h); double h3 = fabs(hMin - 2* h); if (h0 < h) h = h0; if (h2 < h) h = h2; if (h3 < h) h = h3; if (h == 0) h = hMin; if (h < sigma) cond = 1; double e0 = fabs(z0 - yMin); double e1 = fabs(y1 - yMin); double e2 = fabs(y2 - yMin); if (e0 != 0 && e0 < err) err = e0; if (e1 != 0 && e1 < err) err = e1; if (e2 != 0 && e2 < err) err = e2; if (e0 == 0 && e1 == 0 && e2 == 0) err = 0; if (err < epsilon) cond = 2; } double getFunc(DataList &p) { double x = p.at(0); double y = p.at(1); double result = -4 * x + x*x - y - x * y + y * y; return result; } void getDfDx(DataList & de_dxi, DataList &p) { double x = p.at(0); double y = p.at(1); double dfDx = -4+2*x-y; double dfDy = -1-x+2*y; double norm = sqrt(dfDx*dfDx + dfDy*dfDy); dfDx = -dfDx/norm; dfDy = -dfDy/norm; de_dxi.at(0) = dfDx; de_dxi.at(1) = dfDy; } void InitData() { for(int i = 0; i<N; i++) { p1.push_back(0); p2.push_back(0); pMin.push_back(0); de_dxi.push_back(0); } } string stringify(double x) { ostringstream o; if (!(o << x)) return 0; return o.str(); } string CreateResultString(DataList &pMin,double yMin) { string resultStr = "f["; for(int i = 0; i<N; i++) { if (i != 0) resultStr += ","; resultStr += stringify(pMin.at(i)); } resultStr += "] = " + stringify(yMin); return resultStr; }

Ссылки

Литература

Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов. — М.: Высш. шк., 1986.
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М.: Мир, 1985.
Коршунов Ю.М., Коршунов Ю.М. Математические основы кибернетики. — М.: Энергоатомиздат, 1972.
Максимов Ю.А.,Филлиповская Е.А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
Максимов Ю.А. Алгоритмы линейного и дискретного программирования. — М.: МИФИ, 1980.
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.

См. также

Градиентные методы

Wikimedia Foundation. 2010.

Метод градиент
Метод группового учёта аргументов

Смотреть что такое "Метод градиента" в других словарях:

Метод сопряженных градиентов — метод нахождения локального минимума функции на основе информации о её значениях и её градиенте. В случае квадратичной функции в минимум находится за n шагов. Содержание 1 Основные понятия 2 Обосновани … Википедия
Метод сопряжённых направлений — Метод сопряженных градиентов метод нахождения локального минимума функции на основе информации о её значениях и её градиенте. В случае квадратичной функции в минимум находится за n шагов. Содержание 1 Основные понятия 2 Обосновани … Википедия
Метод покоординатного спуска — Содержание 1 Постановка задачи решения системы уравнений в терминах методов оптимизации 2 Градиентные методы … Википедия
Метод одной касательной — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия
Метод Ньютона — Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном… … Википедия
Метод Гаусса — Ньютона — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия
Метод Ньютона-Рафсона — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия
Метод Ньютона — Рафсона — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия
Метод касательной — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия
Метод касательной (Метод Ньютона) — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия

dic.academic.ru

Градиентные методы оптимизации. Градиентный метод первого порядка

Градиентные методы оптимизации - Справочник химика 21

Преимущества градиентного метода оптимизации по сравнению с методом случайного поиска возрастают в случае организации процесса спуска с переменным рабочим шагом. Для этого случая в процессе случайного поиска среднее приращение функции 3(Х) на один расчет в 2л/(и + 1) раз меньше, чем при градиентном методе. Напомним, что п — число оптимизируемых параметров X. Указанные результаты сопоставления детерминированного и случайного способов поиска, естественно, полностью справедливы только для условий выполнения расчетов [56]. Тем не менее, они позволяют сделать вывод о нецелесообразности применения метода случайного поиска для оптимизации непрерывно изменяющихся параметров адсорбционных установок, т. е. там, где возможно использование детерминированных методов направленного поиска (градиентного и др.). Вместе с тем принцип случайного поиска обладает важными преимуществами во-первых, алгоритмы, его реализующие, менее чувствительны, чем детерминированные методы, к наличию неглубоких локальных минимумов, и, во-вторых, некоторые алгоритмы случайного поиска позволяют определить точку абсолютного минимума. [c.136] Аналитические методы являются классическими методами определения экстремального значения функции (минимума или максимума). Они применяются, когда оптимизируемые функции заданы аналитически и число независимых переменных невелико. При большом числе переменных возникает так называемый барьер многомерности и применение аналитических методов становится затруднительным. Затрудняет применение аналитических методов также наличие ограничений. Вследствие этого использование аналитических методов в их классическом виде на практике довольно ограничено. Краткая характеристика этих методов приведена ниже. Принцип максимума для удобства изложения описан после характеристики градиентных методов оптимизации. [c.141]

Градиентные методы оптимизации [c.153]

ГРАДИЕНТНЫЕ МЕТОДЫ ОПТИМИЗАЦИИ [c.222]

Градиентные методы оптимизации относятся к численным методам поискового типа. Они универсальны, хорошо приспособлены для работы с современными цифровыми вычислительными [c.222]

Градиентные методы оптимизации относятся к численным методам поискового типа. Эти методы универсальны, хорошо приспособлены для современных цифровых вычислительных машин и весьма эффективны в большинстве случаев поиска экстремального значения нелинейных функций с ограничениями и без них, а также, когда функция вообще аналитически неизвестна. Вследствие этого градиентные или поисковые методы широко применяются на практике. [c.126]

Подробнее остановимся па методах оптимизации, связанных с нахождением по крайней мере первых производных, которые кажутся нам наиболее перспективными. Эти методы применимы для дифференцируемых функций и используют явные выражения для градиента, причелг в экстремальной точке градиент должен быть равен нулю. Это условие и дает систему уравнений, решение которой основано на методах onTHNiHsauHH. Заметим, что отличие одного градиентного метода оптимизации от другого может быть большим, чем от соответствующего метода решения с использованием уравнений ЗДМ. [c.24]

Крумм Л. А., Градиентный метод оптимизации режима объединенных энергосистем, Электричество, № 5 (1963). [c.216]

С развитием и массовым распространением высокоэффективных градиентных методов оптимизации геомет1ии молекул к настоящему времени накоплено значительное количество новых, бодее корректных результатов неэмпирических квантовохимических расчетов, позволяющих вычислить дополнительные значения сродств к протону. [c.5]

chem21.info

2.1. Градиентные методы. Градиентный метод оптимизации