Численные методы и оптимизация. Численные методы и методы оптимизации
| Объявления | |||||
| ВАЖНО! Прочтите перед написанием сообщения в этот раздел! | PAV | 1 | 1514 | 12.02.2012, 16:34 PAV | |
| Темы | |||||
| Учебники и задачники по методам оптимизации | samson4747 | 5 | 2698 | 08.12.2013, 18:45 roman_slepnev | |
| Учебники и сборники задач по вариационному исчислению | Bridgeport | 1754 | 30.01.2013, 16:42 Bridgeport | ||
| Получить второй порядок аппроксимации (разностная схема) [ На страницу: 1, 2 ] | netang | 15 | 928 | 13.10.2018, 15:39 Eugeen1948 | |
| Неявный метод Рунге Кутта для решения жесткой системы ДУ | Antistas | 13 | 2596 | 13.10.2018, 15:23 Eugeen1948 | |
| Транспортная задача и NP [ На страницу: 1, 2 ] | max(Im) | 17 | 1528 | 14.09.2018, 08:22 Gregory G | |
| Извлечение квадратного корня вручную | Энер | 4 | 3869 | 15.08.2017, 02:36 GAA | |
| Помогите с зацикливанием симплекс-метода [ На страницу: 1, 2 ] | slimsaw | 21 | 2770 | 03.05.2017, 00:47 Andrey_Kireew | |
| Максимальная площадь [ На страницу: 1, 2 ] | alcoholist | 21 | 1389 | 31.12.2016, 10:11 atlakatl | |
| Симплекс-метод и ЛП в целом.. | PeanoJr | 5 | 948 | 20.09.2016, 13:11 falazure123 | |
| "Метод Лобачевского-Греффе" для решения алгебраических уравн [ На страницу: 1, 2 ] | Sverest | 15 | 2100 | 22.05.2016, 16:54 ansh | |
| Аппроксимация ортогональными полиномами [ На страницу: 1, 2 ] | tgv | 15 | 3485 | 24.12.2015, 16:17 Евгений Машеров | |
| Помогите придумать апроксимацию [ На страницу: 1, 2, 3 ] | B@R5uk | 40 | 5541 | 11.08.2015, 22:16 Yahot | |
| Приближённое вычисление смешанной производной 2-го порядка | Mr. Demetrius | 8 | 1758 | 07.08.2015, 11:07 Pumpov | |
| Алгоритм решения уравнения методом прогонки для 3х многого [ На страницу: 1, 2 ] | IRIKA | 16 | 912 | 12.06.2015, 19:54 vasya321 | |
| Промерзание грунта | RAEman | 28 | 1206 | 02.06.2015, 18:29 RAEman | |
| Разностная схема для уравнения переноса. Монотонность | Challenger | 8 | 486 | 30.05.2015, 21:05 Challenger | |
| Операции с матрицами | Aarnikotka | 4 | 369 | 22.05.2015, 10:14 ИСН | |
| Асимптотическая нормальность | vlad_light | 0 | 185 | 21.05.2015, 14:42 vlad_light | |
| Неравноточные измерения | vlad_light | 2 | 226 | 20.05.2015, 21:42 vlad_light | |
| МНК для f=A*sin(2*pi*f*t + phi) + b [ На страницу: 1, 2 ] | kolchenkov | 23 | 1044 | 20.05.2015, 08:36 Евгений Машеров | |
| LASSO | Vandaler | 3 | 327 | 06.05.2015, 21:09 мат-ламер | |
| Квадратичная интерполяция-экстраполяция для экстремума | robot80 | 14 | 662 | 04.05.2015, 14:37 robot80 | |
| Метод простой итерации [ На страницу: 1, 2 ] | integer | 25 | 1090 | 03.05.2015, 19:47 one man | |
| Есть ли способы уменьшить погрешность измерений | Learner | 8 | 509 | 29.04.2015, 23:25 Евгений Машеров | |
| Измерения | Learner | 3 | 293 | 28.04.2015, 19:53 grizzly | |
| Нахождение экстремумов функции нескольких переменных | Aiyyaa | 7 | 553 | 27.04.2015, 20:16 mihailm | |
| Слабая формулировка уравнений мелкой воды [ На страницу: 1, 2, 3 ] | VMMF | 31 | 1906 | 26.04.2015, 18:26 VMMF | |
| Подскажите где найти оценку Метода Монте-Карло. | yaneblinchik | 4 | 290 | 25.04.2015, 21:16 dsge | |
| Исследовать устойчивость явной схемы | netang | 8 | 500 | 12.04.2015, 17:27 мат-ламер | |
| Решение кубического уравнения аналитическим способом. | Punisher174 | 8 | 886 | 10.04.2015, 22:25 Punisher174 | |
| МНК [ На страницу: 1, 2, 3, 4 ] | rlsp | 55 | 2201 | 01.04.2015, 22:05 Евгений Машеров | |
| Уравнение | VladQ | 7 | 592 | 30.03.2015, 01:08 VladQ | |
| Погрешность наклона аппроксимирующей прямой? | bastak | 13 | 939 | 26.03.2015, 07:04 Евгений Машеров | |
| Метод наименьших квадратов | cool.phenon | 5 | 490 | 22.03.2015, 10:59 profrotter | |
| Посоветуйте литературу по вариационному исчислению | tpm01 | 8 | 1941 | 14.03.2015, 22:25 tyrjoy | |
| Уравнения с переменной в показателе степени | Anton_Peplov | 6 | 474 | 12.03.2015, 23:10 Евгений Машеров | |
| Найти экстремумы, определитель матрицы Гессе вырожден | integral2009 | 14 | 2841 | 10.03.2015, 23:04 ewert | |
| численное решение уравнения теплопроводности | molblox | 5 | 348 | 04.03.2015, 20:36 Vince Diesel | |
| Система СДУ (метод Эйлера-Маруямы) | Smoker | 1 | 276 | 01.03.2015, 19:00 Brukvalub | |
| ЗЛП про карандаши | Baskura | 3 | 347 | 23.02.2015, 15:01 ИСН | |
| Аппроксимация с нормой L1 | renegator | 7 | 574 | 12.02.2015, 14:14 Евгений Машеров | |
| Задача на условный экстремум | izirekter | 6 | 447 | 05.02.2015, 22:53 izirekter | |
| Метод сопряженных направлений нулевого порядка | netang | 6 | 598 | 02.02.2015, 21:30 netang | |
| Ошибка полиномиальной интерполяции | B@R5uk | 2 | 390 | 23.01.2015, 15:01 B@R5uk | |
| Применение численных методов | MOEVM | 7 | 573 | 22.01.2015, 17:53 dsge | |
| Модифицированный симплекс-метод | Damir(2) | 3 | 399 | 20.01.2015, 15:24 Damir(2) | |
| Разностные производные | SteelRend | 6 | 626 | 19.01.2015, 22:44 Утундрий | |
| Метод дробления шага | netang | 7 | 769 | 14.01.2015, 08:53 netang | |
| Аппроксимация данных. | fizik_ku | 2 | 483 | 16.12.2014, 21:12 mserg | |
| Аппроксимация рядом экспонент. | fizik_ku | 5 | 708 | 16.12.2014, 00:25 fizik_ku | |
dxdy.ru
Численные методы оптимизации и их виды.
Введение
Математические методы применяются для создания математических моделей исследуемых отраслей промышленности, строительстве, сельском хозяйстве и др.
Численные методы в теоретическом аспекте делятся на следующие :
1) Линейное программирование;
2) Нелинейное программирование;
3) Динамическое программирование.
Выше приведенные задачи математического программирования встречаются во всех отраслях промышленности и производства, связанные с управляющим расчетами, целью оптимального планирования и прогнозирования развития исследуемой отрасли.
Построение математических моделей.
Задача использования сырья. Для изготовления двух видов продукции Р1,Р2 используют три вида сырья: S1,S2 и S3. Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также величина прибыли, получаемая от реализации единицы продукции, приведены в табл.1. Необходимо составить такой план выпуска продукции, чтобы при ее реализации получить максимальную прибыль.
Обозначим через x1 количество единиц продукции P1, а через x2 - количество единиц продукции P2. Тогда, учитывая количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также запасы сырья, получим систему ограничений
2x1+5x2 £ 20,
8x1+5x2 £ 40,
5x1+6x2 £ 30,
которая показывает, что количество сырья, расходуемое на изготовление продукции, не может превысить имеющихся запасов. Если продукция P1 не выпускается, то x1=0 ; в противном случае x1>0. То же самое получаем и для продукции P2. Таким образом,на неизвестные x1 и x2 должно быть наложено ограничение неотрицательности: x1 ³ 0 , x2³ 0 .
Таблица 1.
| Виды сырья | Запас сырья | Количество единиц сырья, идущих на изготовление единицы продукции | |
| Р1 | Р2 | ||
| S1 | 20 | 2 | 5 |
| S2 | 40 | 8 | 5 |
| S3 | 30 | 5 | 6 |
| Прибыль от единицы продукции, руб | 50 | 40 | |
Конечную цель решаемой задачи - получение максимальной прибыли при реализации продукции - выразим как функцию двух переменных x1 и x2. Реализация х1 единиц продукции вида Р1 и х2 единиц продукции вида дает соответственно 50 х1 и 40 х2 сум. прибыли, суммарная прибыль Z =50 x1+40 x2 (сум).
Условиями не оговорена неделимость единицы продукции, поэтому x1 и x2 (план выпуска продукции) могут быть и дробными числами, следовательно, задача имеет бесконечное множество вариантов планов (значений x1 и x2, которые удовлетворяют системе ограничений). Необходимо найти такие неотрицательные значения x1 и x2 ,при которых функция Z достигает максимума, т.е. найти максимальное значение линейной функции Z=50х1+40x2 при ограничениях
2x1+5x2 £20,
8x1+5x2 £40, x1 ³0, x2 ³ 0.
5x1+6x2 £30,
Построенная линейная функция называется функцией цели и совместно с системой ограничений образует математическую модель рассматриваемой задачи.
Задачу использования сырья можно легко обобщить, если при выпуске n видов продукции используются m видов сырья. Обозначим через Si(i=1,2,…,m) виды сырья; bi - запасы сырья, i -го вида; Pi (i=1,2,…,n) -виды продукции; aij -количество единиц i - го сырья, идущего на изготовление единицы j - й продукции; Cj - величину прибыли, получаемой при реализации единицы j - продукции. Условия задачи запишем в табл.2.
Таблица 2.
| Виды сырья | Запас сырья | Количество единицы i-го сырья идушего на изготовление единицы j-й продукции | |||
| Р1 | Р2 | … | Pn | ||
| S1 | b1 | a11 | a12 | … | a1n |
| S2 | b2 | a21 | a22 | … | a2n |
| … | … | … | … | … | … |
| Sm | bm | am1 | am2 | … | amn |
| Прибыль | С1 | С2 | … | Сn | |
Пусть xj - количество единиц j-й продукции, которое необходимо произвести. Тогда математическую модель задачи можно представить в следующем виде.
Найти максимальное значение линейной функции
Z=C1x1+C2x2 +…+Cnxn при ограничениях
a11x1+a12x2+…+a1nxn£b1,
a21x1+a22x2+…+a2nxn£b2,
. . . . . . . . . . . . . . . . . . . bi³0 (i=1,2,…,m),
am1x1+am2x2+…+amnxn£bm, xj³ (j=1,2,…,n).
Задача составления рациона. При откорме каждое животное ежедневно должно получить не менее 9 ед. питательного вещества S1, не менее 8 ед. Вещества S2 и не менее 12 ед. вещества S3. Для составления рациона используют два вида корма. Содержание количества единиц питательных веществ в 1 кг каждого вида корма и стоимость 1 кг корма приведены в табл.3.
Т а б л и ц а 3.
| Питательные вещества | Кол-во единиц питательных веществ в 1 кг корма | |
| Корм I | Корм II | |
| S1 | 3 | 1 |
| S2 | 1 | 2 |
| S3 | 1 | 6 |
| Стоимость 1кг корма , коп. | ||
Необходимо составить дневной рацион нужной питательности,причем затраты на него должны быть минимальными.
Для составления математической модели обозначим через x1 и x2 cсоответственно количество килограммов корма I и II в дневном рационе. Принимая во внимание значения, приведенные в табл.3. и условие, что дневной рацион удовлетворяет требуемой питательности только в случае, если количество единиц питательных веществ не меньше предусмотренного, получаем систему ограничений
3x1+x2 ³9,
x1+2x2 ³8, x1³0,x2³0.
Если корм I не используется в рационе, то x1=0 в противном случае x1>0. Аналогично имеем x2³0 т.е. должно выполнятся условие неотрицательности переменных: x1³0,x2³0 .
Цель данной задачи - добиться минимальных затрат на дневной рацион, поэтому общую стоимость рациона можно выразить в виде линейной функции Z=4x1+6x2 (коп). Задача является многовариантной, x1 и x2 могут принимать бесконечное множество значений. Из этого множества следует выбрать такие x1 и x2 , при которых функция Z принимает минимальное значение. Таким образом, необходимо найти минимальное значение линейной функции Z=4x1+6x2 при
ограничениях
3x1+x2 ³9,
x1+2x2 ³8, x1³0, x2 ³0.
X1+6x2 ³12,
Задачу составления рациона можно обобщить, если предусмотреть в рационе m видов питательных веществ количестве не менее bi (i=1,2,…,m) (ед) и использовать n видов кормов. Для составления математической модели задачи обозначим через aij (i=1,2,…,m;j=1,2,…,n) кол-во единиц i-го питательного вещества, содержащегося в единице j-го корма; Cj - стоимость единицы j-го корма; xj - кол-во единиц j-го корма в дневном рационе.
Необходимо найти минимальное значение линейной функции Z=C1x1+C2x2+…+Cnxn при ограничениях
a11x1+a12x2+…+a1nxn³b1,
a21x1+a22x2+…+a2nxn³b2,
………………………… xj³0 (j=1,2,…,n),
am1x1+am2x2+…+amnxn³bm, bi³0 (i=1,2,…,m).
Рассматривая приведенные задачи и их математические модели, нетрудно заметить, что если потребовать, чтобы в процессе производства какое-то сырье использовалось полностью или в дневном рационе должно содержаться точное кол-во единиц какого-нибудь питательного вещества, то ограничение для этого сырья (питательного вещества) можно выразить в виде уравнения.
Таким образом, системы ограничений в зависимости от условий задачи могут содержать не только линейные неравенства, но и линейные уравнения. При решении систем линейных неравенств с n неизвестными приходится сталкиваться с большими трудностями, поэтому от неравенств переходят к равенствам и решают систему линейных уравнений. Этот метод широко применяют при решении задач линейного программирования.
aim.uz
Численные методы и оптимизация
Московский технический университет по связи и информатике
Заочная форма обучения
Курсовая работа по предмету:
Информатика
Тема: Численные методы и оптимизация
Студента 2 курса
Специальности 201000
Студенческий билет
№
Преподаватель:
2004 год
Задание
1. Для заданной функции y(x) методом наименьших квадратов для степенного базиса получить линейную F1(x) = a0 + a1x и квадратичную F2(x) = a0 + a1x + a2x2 аппроксимирующие функции:
- составить и решить систему нормальных уравнений;
- определить параметры аппроксимирующих функций;
- вычислить значения аппроксимирующих функций в узлах аппроксимации;
- построить график заданной функции (множество точек) и графики функций линейной и квадратичной аппроксимации;
- оценить качество аппроксимации.
2. Найти два корня уравнения F2(x) = 0 с заданной точностью Е:
- отделить корни;
- проверить (аналитически) условия сходимости применяемых методов решения уравнений. В случае необходимости привести уравнение к виду, обеспечивающему сходимость процесса приближения к корню;
- выбрать начальное приближение;
- записать рекуррентную формулу для уточнения корня;
- оценить погрешность.
3. Вычислит dx при разбиении отрезка интегрирования на
n1 = 10 и n2 = 20 подынтервалов , x1, x2 - корни уравнения :
- оценить погрешность.
4. Определить точку экстремума функции F2(x) методами одномерной оптимизации (с точностью Е):
- проверить условие унимодальности и выбрать начальный отрезок оптимизации;
- записать условие окончания поиска минимума (максимума) функции.
Задание 1. Функция y = y(x) задана таблицей.
Таблица 1
|
I |
0 |
1 |
2 |
3 |
4 |
5 |
|
xi |
0 |
2 |
4 |
6 |
8 |
10 |
|
y(x) |
1 |
1.386 |
0.406 |
-0.939 |
-1.286 |
-0.266 |
Запишем параметры линейной аппроксимации:
x = = 4.285 y = = 0.043
a0 = y – a1x = 1.170952
a1 = = -0.2241571
Искомая линейная аппроксимирующая функция:
F1(x) =-0.2241571х+1.170952
Составим и решим систему нормальных уравнений для определения параметров многочлена второй степени F2(x) = a0 + a1x + a2x2
(n+1)a0 + ( Σxi )a1 + ( Σxi2)a2 = Σ yi
( Σxi )a0 + ( Σxi2)a1 + ( Σx3)a2 = Σ xi yi
(Σxi2)a0 + ( Σxi3 )a1 + ( Σxi4)a2 = Σ xi2 yi .
Система нормальных уравнений:
6а0 30а1 + 220а2 = 0.301
30а0 + 220а1 - 1800а2 = -14.186
220а0 - 1800а1 + 15664а2 = -130.668
Решение системы нормальных уравнений:
а2 = 2.545535Е-02 а1 = -0.4787107 а0 = 1.510357
Искомая аппроксимирующая функция:
F2(x) = 2.545535E-02x2– 0.4787107 x1.510357
Значения аппроксимирующих функций F1{x} и F2{x} в узлах аппроксимации приведены в таблице 3:
|
X |
0 |
2 |
4 |
6 |
8 |
10 |
|
F1{x} |
1.170952 |
0.722638 |
0.274323 |
-0.1739 |
- 0.6223 |
-1.0706 |
|
F2{x} |
1.51035 |
0.65475 |
2.799E-03 |
-0.4455 |
-0.6901 |
-0.7312 |
Таблица3
Графики функций линейной и квадратичной аппроксимации показаны на рисунке
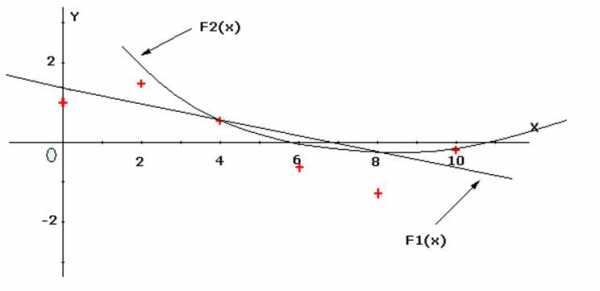
Оценим качество аппроксимации:
ρ = sqr(1/(n+1)* ∑ (Fm(xi) – y(xi))2)
Для линейной функции: р1=0.5999658
Для квадратичной функции: р2=0.5435526
p2<p1, значит аппроксимация квадратичной функции более качкственная.
Задание 2. Решение уравнения F2(x) с точностью Е = 10-4. Для отделения корней уравнения F2(x)
составим таблицу знаков функции F2(x).
Таблица 4
|
X |
-1 |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
|
Sign F2(x) |
+ |
+ |
+ |
- |
- |
- |
- |
- |
+ |
На отрезках [3 5] и [12 15] функция F2(x) меняет знаки, т.е. существует, по крайней мере, по одному корню.
Производная F2'(x) = 0.051x-0.4787107,
F2"(x) = 0.051 > 0, следовательно, производная F2'(x) - монотонно возрастающая функция.
Составим таблицу знаков функции Аэ(ч) на выбранных отрезках:
|
X |
3 |
5 |
13 |
15 |
|
Sign F2’(x) |
-0.32571 |
-0.2237 |
0.18423 |
0.2863 |
vunivere.ru