Содержание
Метод рейтинга/ранжирования
Второй сравнительный метод стоимостной
оценки – метод рейтинга/ранжирования23.
Свое название метод получил от одной
из итераций, когда для определения
степени «схожести» оцениваемого объекта
с аналогом используют сравнительную
шкалу.
Этот метод в сочетании с доходным нашел
широкое применение в методиках
Роспатента.24
Однако в частных случаях его используют
лишь как вспомогательный.
Метод Рейтинга/Ранжирования состоит
из следующих четырех этапов:
Подбор наиболее похожего брэнда, чья
стоимость известна.Составление критериев оценки брэнда,
объединяющихся в определенную систему.Выставление оценки, ее взвешивание и
нормализация.Расчет стоимости брэнда.
Отличительной чертой этого метода
является его экспертный, т. е. субъективный
е. субъективный
характер. Чтобы получать как можно более
объективное значение, важно выбрать и
приспособить для своих нужд какую-то
одну систему. В качестве примера
использования метода рейтинга/ранжирования
можно привести оценку брэнда «Евро-Нова»
по системе критериев Interbrand
(ТАБЛИЦА 6.).
Оценка брэнда
«Евро-Нова» по системе критериев
компании Interbrand
Вес (1-5) | Баллы (1-5) | Взвешенные баллы | |
1. Лидерство | 5 | 3 | 15 |
2. Стабильность | 3 | 4 | 12 |
3. | 2 | 4 | 8 |
4. Интернациональность | 5 | 2 | 10 |
5. Модность | 2 | 5 | 10 |
6. Поддержка | 2 | 3 | 6 |
7. Защита | 1 | 5 | 5 |
66 |
Источник:
Козырев А. Н., Макаров В.Л. Оценка стоимости
Н., Макаров В.Л. Оценка стоимости
нематериальных активов и интеллектуальной
собственности. – М.: РИЦ ГШ ВС РФ, 2003. –
368 с./ 2003.
Процедура оценки выглядит следующим
образом: сначала брэнд оценивается по
каждому из критериев, затем оценка
взвешивается в соответствии со степенью
важности критериев, и полученные
результаты суммируются. В завершение
взвешенную оценку в баллах нормализуют
по оценке сопоставимого брэнда. В
приведенном примере результат 66
масштабируется по сравнению с эталонным
тестом. Например, если бы все оценки для
сопоставимого брэнда были равны 3, то
полная взвешенная оценка «Евро-Новы»
была бы равна 60 или 3,3, что немногим
лучше, чем удовлетворительно.
На первый взгляд метод рейтинга/ранжирования
обладает большим количеством недостатков,
чем достоинств.
Очевидно, что он субъективен. Однако
если привлекается достаточное количество
независимых оценщиков, то оценка может
считаться достаточно объективной.
Результат зависит от подбора критериев.
В приведенном примере брэнд Евро-Нова
получил скромную оценку, поскольку
оценивался по системе критериев,
разработанных для компаний-претендентов
на мировое лидерство.Возможность использования весового
коэффициента как прямого множителя
является спорным и зависит от
обоснованности предположения о линейной
шкале. Если бы полученная в примере
оценка в баллах составила 1, то в данной
системе это означало бы, что товарный
знак практически ничего не стоит, то
есть 0, а не 33% от стоимости сопоставимой
сделки.Метод можно использовать только при
небольших отклонениях в оценках.
Недопустимо его использование, если
какой-либо фактор имеет фатальный
недостаток. Хорошей альтернативой
считается использование каждого
критерия в отдельности. Например, если
все остальные показатели примерно
совпадают, но существует двукратная
разница в прибыли до налогообложения,
то на основе этого, теоретически, можно
говорить, что стоимость будет различаться
в два раза.
Между тем метод рейтинга/ранжирования
представляет собой определенную ценность
по ряду причин:
Он удобен в использовании, особенно,
при использовании хороших эталонных
тестов. При увеличении опыта оценки
стоимости брэндов и наличии широкой
базы данных, этот метод может давать
качественные сравнения и оценки.Он непосредственно связывается с
рыночной стоимостью, характеризуя
различия между оцениваемыми объектами;
в процессе оценки выявляются факторы,
которые могут способствовать росту
стоимости брэнда.Он является хорошим тестом для выяснения
результатов маркетинга. Также он
достаточно доступен в объяснении
неспециалистам.
Актуальность корректной расстановки весовых коэффициентов в задачах классификации радиолокационных целей | Делов
Аннотация
Рассмотрены методы расстановки весов, определяющих степень доверия к априорной информации по движущимся радиолокационным объектам. Поставлен вопрос об автоматизации данной задачи. Предложен алгоритм расчета весов, позволяющий программно рассчитать весовые коэффициенты. Приведен пример расчета весов для любого количества классов и любого количества эталонов с помощью разработанной авторами компьютерной программы
Поставлен вопрос об автоматизации данной задачи. Предложен алгоритм расчета весов, позволяющий программно рассчитать весовые коэффициенты. Приведен пример расчета весов для любого количества классов и любого количества эталонов с помощью разработанной авторами компьютерной программы
Введение
В системах, основанных на принятии разного рода решений в многопризнаковом пространстве, одним из основных элементов является функция правдоподобия, в общем случае представляющая собой функцию, которая зависит от определенного параметра (признака) при фиксированном событии. Таким образом, функция правдоподобия показывает, насколько правдоподобен выбранный параметр при заданном событии.
Для определенного класса распознаваемого движущегося радиолокационного объекта с рассматриваемым признаком х можно определить функцию правдоподобия, представляющую собой смешанную модель и состоящую из конечного числа некоторых распределений, описываемую формулой
где g — количество смешиваемых компонент; ωj ≥ 0 — весовой коэффициент
определяющий важность (вес) компоненты, входящей в рассматриваемую модель;
f(х, θj), j = 1,. ..,g — компонента функции плотности условного распределения, зависящая от вектора θj.
..,g — компонента функции плотности условного распределения, зависящая от вектора θj.
Компоненты функции плотности условного распределения базируются на знаниях данных образующих процессов. Например, для смешанной нормальной модели f(х, θj) — условная плотность, распределенная по нормальному закону [1].
Далее рассмотрим подробнее методы расчета самих весовых коэффициентов, но для начала опишем некоторые задачи, при которых используются веса ωj :
- нормировка признаков, заключающаяся в преобразовании полученных данных к новой форме представления, которая позволяет исключить влияние на итоговый результат анализа принятых единиц измерения;
- задание степени важности признаков, т. е. наиболее важному признаку или классу приписывается б0льшее значение коэффициента;
- отбор признаков (ω j = 1), позволяющий рассматривать только необходимые классы или признаки, что упрощает задачу классификации, сокращая время работы некоторых алгоритмов.

Рассмотрим некоторые методы расчета весовых коэффициентов. Эти методы используются для определения важности цели и разбивают исследуемые объекты по уровням предпочтения. Формирование этих уровней происходит от одной наиболее опасной цели [2].
Метод ранжирования
Данный метод позволяет упорядочить компоненты по степени возрастания или убывания их влияния в зависимости от особенностей рассматриваемого события. Результаты ранжирования n компонент m экспертами можно представить в виде табл. 1.
Оценку важности той или иной компоненты проводит группа специализированных экспертов, и каждый из них представляет свой вектор оценок по данной группе компонент, основываясь на знаниях в области слабо формализованных задач. Компоненты расставляются с учетом их важности согласно принятому порядку.
- Эксперт располагает компоненты по убыванию их важности слева направо.
- Каждой компоненте присваивается оценка от n до 1 (самой важной — n и далее по убыванию до 1).

- Для каждой компоненты высчитывается сумма оценок, далее — доля от всех полученных сумм. В виде формулы это можно представить как
где rij — оценка, поставленная j-й компоненте i-м экспертом.
Таким образом, весовой коэффициент ω j определяется как отношение суммы мнений экспертов по j-й компоненте к сумме мнений экспертов по всем показателям [3].
Метод непосредственной оценки
В основе метода — оценка экспертами важности частной компоненты по определенной шкале, например, от 0 до 10, поэтому метод непосредственной оценки иногда называют балльным методом или методом прямой расстановки. При этом разрешается оценивать важность дробными величинами или приписывать одну и ту же величину из выбранной шкалы нескольким компонентам. Таблица оценок представлена так же, как и в предыдущем методе (см. табл. 1).
Таблица 1
Результаты опроса экспертов по рассматриваемым компонентам
Эксперт | Рассматриваемые компоненты | |||
|---|---|---|---|---|
x1 | x2 | . | xn | |
1 | r11 | r12 | … | r1n |
2 | r21 | r22 | … | r2n |
… | … | … | … | … |
M | rm1 | rm2 | … | rmn |
Алгоритм расчета весовых коэффициентов следующий:
- Каждый эксперт проставляет оценки по всем компонентам в рамках заданной шкалы.
- Происходит пересчет оценок по формуле
- Далее, как и при методе ранжирования, полученные оценки для каждой компоненты суммируются и нормируются.
Разработка алгоритма перерасчета весовых коэффициентов
Результаты классификации с весами, полученными по изложенным выше методам, могут отличаться от ожидаемых, поэтому возникает необходимость коррекции весов. Этот этап отладки может занимать очень длительное время. Увеличение количества классов или компонент функции правдоподобия также затрудняет правильную расстановку весовых коэффициентов.
Этот этап отладки может занимать очень длительное время. Увеличение количества классов или компонент функции правдоподобия также затрудняет правильную расстановку весовых коэффициентов.
Рассмотрим метод расчета, позволяющий решить эти проблемы.
Так как объект находится в движении, измеряемые значения признаков будут меняться, поэтому при определении опасности по каждой цели целесообразно использовать накопительную функцию, которая будет состоять из g компонент на фиксируемых участках измерения определенного признака, назовем их эталонами.
В общем случае все весовые коэффициенты можно представить с помощью табл. 2.
Таблица 2
Таблица весовых коэффициентов для каждого класса
Эталон | Рассматриваемые классы | |||
|---|---|---|---|---|
Класс 1 | Класс 2 | … | Класс n | |
x1 | w11 | w12 | . | w1n |
x2 | w21 | w22 | … | w2n |
… | … | … | … | … |
xm | wm1 | wm2 | … | wmn |
В качестве оценок эксперта при коррекции весовых коэффициентов будет выступать ожидаемая вероятность (табл. 3) соотнесения измеренного признака с его эталоном.
Таблица 3
Таблица вероятностей на определенных участках измерения
Эталон | Рассматриваемые классы | |||
|---|---|---|---|---|
Класс 1 | Класс 2 | … | Класс n | |
x1 | p11 | P12 | . | P1n |
x2 | P21 | P22 | … | P2n |
… | … | … | … | … |
xm | P1m | Pm2 | … | Pmn |
Для уточнения весовых коэффициентов (рисунок) был выбран алгоритм коррекции ошибок, использующийся в теории нейронных сетей. Его принцип состоит в следующем:
- Текущее значение сравнивается с желаемым выходом.
- Если разница между ними превосходит заданную величину ошибки определения опасности, идет перерасчет весов.
Рисунок. Процесс перерасчета весовых коэффициентов
Далее п. 1, 2 повторяются.
Ошибку определения опасности можно найти по формуле
Здесь — ожидаемая вероятность соотнесения измеренного признака с его эталоном;
— текущее значение вероятности, определяемое по формуле
где P( Aj) — априорная вероятность;
M — число эталонов;
N — количество классов.
Обозначим текущее значение веса как ωij (n), соответствующее i-му классу и j-му эталону, на n-м шаге обучения. В соответствии с дельта-правилом изменение Δωϋ (n), применяемое к данному весу ωj (n) на этом шаге дискретизации, задается выражением
где η — некоторая положительная константа, определяющая скорость обучения и используемая при переходе от одного шага процесса к другому, которую естественно именовать параметром скорости обучения.
Вычислив величину веса Δωij (n), можно определить его новое значение для следующего шага дискретизации [4]:
На основе этого алгоритма была реализована компьютерная программа расчета весовых коэффициентов (см. рисунок).
Данная программа позволяет рассчитывать весовые коэффициенты для любого количества классов и эталонов, кроме того, она позволяет задавать ошибку перерасчета Ei и параметр скорости обучения η.
Данные были получены не случайным образом, а в результате опроса специалистов и имеют определенный уровень достоверности, поэтому в качестве ошибки можно взять эту достоверность, а также точность, с которой проходит перерасчет весовых коэффициентов. Программа расчета весовых коэффициентов для систем поддержки принятия решений включает:
Программа расчета весовых коэффициентов для систем поддержки принятия решений включает:
- предварительную нормированную оценку опасности выбранной цели экспертом;
- предварительную инициализацию весов;
- перерасчет весов в соответствии с уровнем предпочтения цели.
Заключение
По результатам анализа методов можно заключить, что самым простым является метод ранжирования. Для его использования достаточно знать лишь приоритеты рассматриваемых компонент, однако с его помощью не удается рассматривать степень различия между этими признаками.
Метод непосредственной оценки позволяет это сделать, благодаря чему можно сортировать/ранжировать компоненты по важности. В некотором роде метод ранжирования можно рассматривать как частный случай метода непосредственной оценки. Для этого метода эксперты выставляют оценки с учетом вероятности существования данной компоненты при рассматриваемом событии. Следовательно, возможен вариант нулевого весового коэффициента, если рассматриваемая компонента при данном событии вообще не имеет значения.
В статье не был рассмотрен метод парного сравнения, в котором составляется квадратная матрица компонент со значением 1, если компонента строки матрицы важнее компоненты столбца, и 0 в противном случае. Однако и при использовании этого метода не учитывается разница в значимости компонент (как и при методе ранжирования).
Рассмотренные в работе методы основаны на теоретической расстановке коэффициентов экспертами, поэтому появилась необходимость разработать и реализовать алгоритм автоматического расчета весов. Основное достоинство программы с этим алгоритмом — быстрое получение весовых коэффициентов. Однако данный метод расчета требует качественного определения априорных вероятностей.
Формула ранга
процентилей | Вычислить процентиль ранга в Excel
Формула процентиля ранга дает процентиль ранга данного списка. В обычных расчетах мы знаем формулу R = p/100(n+1). Однако в Excel мы используем функцию RANK.EQ с функцией COUNT для вычисления процентиля ранга заданного списка.

Процентильный ранг — это процент оценок, равных или может быть меньше заданного значения или оценки. Процентный процент также находится в диапазоне от 0 до 100. Математически он представлен как:
R = P / 100 (N + 1)
Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку с указанием авторства. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: формула процентного ранга (WallStreetMojo.com)
Где
- R = процентный ранг
- P = процентиль
- n = количество предметов
Таблица содержимого
- . 9 место0021
- Explanation
- Examples
- Example #1
- Example #2
- Example #3
- Example #4
- Relevance and Use of Percentile Rank Formula
- Recommended Articles
Explanation
The формула показывает, сколько оценок или наблюдений отстает от определенного ранга. Например, одно наблюдение получает 90 процентилей; это не означает, что оценка наблюдения составляет 90% из 100. Скорее, она указывает, что наблюдение выполнило по крайней мере то, что другие 90% наблюдений выше или выше этих наблюдений. Следовательно, формула включает количество наблюдений, умножает их на процентиль и указывает положение, в котором должно находиться это наблюдение. Таким образом, после того, как данные упорядочиваются от низшего к наибольшему и каждому наблюдению присваивается ранг, мы можем использовать только число, полученное из формулы, и сделать вывод, что наблюдение находится в заданном процентиле.
Например, одно наблюдение получает 90 процентилей; это не означает, что оценка наблюдения составляет 90% из 100. Скорее, она указывает, что наблюдение выполнило по крайней мере то, что другие 90% наблюдений выше или выше этих наблюдений. Следовательно, формула включает количество наблюдений, умножает их на процентиль и указывает положение, в котором должно находиться это наблюдение. Таким образом, после того, как данные упорядочиваются от низшего к наибольшему и каждому наблюдению присваивается ранг, мы можем использовать только число, полученное из формулы, и сделать вывод, что наблюдение находится в заданном процентиле.
Примеры
Вы можете скачать этот шаблон Excel с формулой процентного ранга здесь — Формула процентного ранга Excel Template
Пример #1
Рассмотрим набор данных из следующих чисел: 122, 112, 114, 17, 118, 116, 111, 115, 112. Вам необходимо рассчитать ранг 25-го процентиля.
Решение:
Используйте следующие данные для расчета процентного ранга.
Итак, расчет ранга можно сделать следующим образом:
R = P/100(N+1)
= 25/100(9+1)
Ранг будет:
Ранг = 2,5 й ранг.
Процентильный ранг будет:
Поскольку ранг является нечетным числом, мы можем взять среднее значение 2-го и 3-го членов, что равно (111 + 112)/2 = 111,50.
Пример #2
Уильям, известный врач-зоотехник, в настоящее время работает над здоровьем слонов и находится в процессе создания лекарства для лечения слонов от распространенной болезни, которой они страдают. Но для этого он сначала хочет узнать средний процент слонов, число которых ниже 1185.
- Для этого он отобрал выборку из 10 слонов, вес которых в килограммах следующий:
- Используйте формулу ранга процентиля, чтобы найти 75-й процентиль.
Решение:
Используйте следующие данные для расчета процентного ранга.
Итак, расчет ранга можно сделать так:
R = P / 100 (N + 1)
= 75 / 100 (10 + 1)
Ранг будет:
Ранг = 8,25 ранг.
Процентильный ранг будет следующим:
8 й термин равен 1177, а теперь к этому прибавляем 0,25 * (1188 – 1177), что равно 2,75, и получаем 1179,75.
Процентильный ранг = 1179,75
Пример #3
Институт IIM хочет объявить свой результат для каждого студента в относительных единицах. Они пришли к выводу, что вместо предоставления процентов они хотят дать относительный рейтинг. Данные для 25 студентов. Используя формулу процентного ранга, узнайте, каким будет число 9.6-й процентиль?
Решение:
Количество наблюдений здесь равно 25. Таким образом, нашим первым шагом будет ранжирование данных.
Таким образом, расчет ранга можно сделать следующим образом: будет:
Ранг = 24,96 ранг
Процентиль Ранг будет:
24 -й -й член равен 488, и теперь к этому добавляется 0,96 * (489 – 488), что равно 0,96, и результат равен 488,96.
Пример #4
Теперь определим значение с помощью шаблона Excel для практического примера I.
Решение:
Используйте следующие данные для расчета процентного ранга.
Таким образом, вычисление процентиля ранга может быть выполнено следующим образом:
Перцентиль ранга будет:
Перцентиль ранга = 1179,75
Релевантность и использование процентиля ранга Формула
Процентильные ранги полезны, когда кто-то хочет понять, как конкретная оценка будет сравниваться с другими значениями, наблюдениями или оценками в заданном наборе данных или заданном распределении оценок. Процентили в основном используются в статистике и образовании, где вместо того, чтобы предоставлять учащимся соответствующие проценты, они показывают их относительные рейтинги. И если кто-то заинтересован в относительном ранжировании, то средние, фактические значения или дисперсия, которая является стандартным отклонением, будут бесполезны. Итак, мы можем сделать вывод, что процентильный ранг дает вам картину относительно других, всегда не абсолютное значение или ответ относительно других наблюдений, а не о среднем значении. Кроме того, некоторые финансовые аналитики используют этот критерий, чтобы отобрать акции, где они могут использовать любой из ключевых финансовых показателей и выбрать акции, которые находятся в 9-м диапазоне.0-й процентиль.
Итак, мы можем сделать вывод, что процентильный ранг дает вам картину относительно других, всегда не абсолютное значение или ответ относительно других наблюдений, а не о среднем значении. Кроме того, некоторые финансовые аналитики используют этот критерий, чтобы отобрать акции, где они могут использовать любой из ключевых финансовых показателей и выбрать акции, которые находятся в 9-м диапазоне.0-й процентиль.
Рекомендуемые статьи
Эта статья представляет собой руководство по формуле процентного ранга. Мы узнали, как рассчитать процентиль в Excel, используя практические примеры и загружаемый шаблон Excel. Вы можете узнать больше о моделировании в Excel из следующих статей: –
- Формула процентиля ExcelФормула процентиля ExcelФункция ПРОЦЕНТИЛЬ отвечает за возврат n-го процентиля из предоставленного набора значений. читать далее
- РАНГ в ExcelРАНК В ExcelExcel Формула ранга дает ранг данного набора данных чисел. Функция ранжирования была встроенной функцией в Excel 2007 и более ранних версиях; теперь у нас есть функции Rank.
 Avg и Rank.Eq в последующих версиях выше 2007 года.Подробнее
Avg и Rank.Eq в последующих версиях выше 2007 года.Подробнее - Формула среднего диапазона Формула среднего диапазона Формула среднего диапазона используется для вычисления среднего значения двух заданных чисел, и в соответствии с формулой данные два числа складываются, а результат делится на 2, чтобы получить среднее значение двух. читать далее
- Формула ФормулаСтандартное нормальное распределение представляет собой симметричное распределение вероятностей относительно среднего или среднего значения, показывающее, что данные, близкие к среднему или среднему, встречаются чаще, чем данные, далекие от среднего или нормы. Таким образом, оценка называется «Z-оценка». Подробнее о стандартном нормальном распределении стандартного нормального распределенияСтандартное нормальное распределение представляет собой симметричное распределение вероятностей относительно среднего или среднего значения, показывающее, что данные, близкие к среднему или среднему, встречаются чаще. часто чем данные далеки от среднего или нормы.
 Таким образом, оценка называется «Z-оценка».Подробнее
Таким образом, оценка называется «Z-оценка».Подробнее - Excel. критерии1, …).читать далее
Как рассчитать и оценить эффективность сотрудников – Блог Clockify
Калькулятор рейтинга эффективности сотрудников делает процесс оценки сотрудников более удобным. В зависимости от политики компании, такую оценку сотрудников проводят работодатели или менеджеры.
В этом блоге мы поговорим о преимуществах использования калькулятора оценки эффективности сотрудников, его основных компонентах, а также о нескольких методах расчета, которые вы можете использовать. Вы также сможете загрузить и использовать наши бесплатные калькуляторы рейтинга производительности, которые прилагаются к каждому обсуждаемому методу расчета.
Содержание
Что такое калькулятор рейтинга эффективности сотрудников?
Этот калькулятор может включать различные разделы оценок, такие как Компетенции, Цели производительности, Цели развития и другие. Внутри каждой из этих секций есть несколько элементы контента . Этими элементами могут быть индивидуальные качества, навыки или квалификация работников. Вы можете включить любое качество или навык, который вы хотите.
Этими элементами могут быть индивидуальные качества, навыки или квалификация работников. Вы можете включить любое качество или навык, который вы хотите.
Как руководитель вы должны изучить каждый элемент контента и каждый раздел, чтобы проанализировать производительность сотрудников и качество их работы. Результаты этих оценок собраны в рабочем документе . Это онлайн-документ, который содержит оценки сотрудников за определенный период.
Преимущества использования калькулятора оценки эффективности сотрудников
Калькулятор рейтинга сотрудников делает процесс оценки сотрудников более удобным. Вот основные причины, по которым вам стоит попробовать этот калькулятор:
- Он прост в использовании, и все расчеты выполняются автоматически.
- Поскольку вы будете анализировать всех своих сотрудников по одному шаблону, вы будете способствовать прозрачности и равенству среди сотрудников.
- Результаты, которые вы получите после оценки, прояснят, нуждаются ли некоторые сотрудники в улучшении в определенных областях.
 Но он также представит лучших исполнителей.
Но он также представит лучших исполнителей.
Если вы все еще не уверены, какой метод использовать, вот наши предложения:
- Усредненный метод без взвешивания — это идеальное решение, если вам нужен простой способ оценки эффективности сотрудников без слишком подробного анализа. анализы.
- Усредненный метод с взвешиванием — если вы хотите подчеркнуть важность отдельных элементов работы сотрудника, выберите этот метод.
Каковы основные компоненты калькулятора оценки эффективности сотрудников?
Прежде чем мы покажем вам, как измерить производительность сотрудников с помощью калькулятора, давайте рассмотрим основные компоненты этого калькулятора.
Элемент контента – как мы уже упоминали ранее, это качество, навык или квалификация работника. Это качества, которые оцениваются.
Разделы – каждый раздел включает несколько элементов контента, принадлежащих к одной группе. Например, раздел «Компетентность» или «Цели эффективности».
Модели рейтинга — шкала, по которой вы оцениваете элементы содержания сотрудника. Диапазон от 1 до 5. Таким образом, цифра 5 — это максимальный числовой рейтинг .
Компетенции – это все качества, которыми должны обладать сотрудники при работе на той или иной должности. Например, навыки, необходимые для этой должности, их знание какого-либо программного обеспечения или языка или атрибут.
Цели производительности – цель этих целей состоит в том, чтобы определить, насколько хорошо сотрудник справляется с заранее определенными целями.
Вес — не все элементы контента имеют одинаковую ценность. Таким образом, лучший способ разделить их — добавить каждому элементу разный вес. Веса обычно добавляются, когда в разделах есть действия, не поддающиеся количественной оценке, такие как усилия или командная работа.
Сумма всех весов элементов контента в одном разделе должна быть равна 100. Помимо элементов, веса могут иметь и сами разделы. Сумма всех весов секций в исполнительном документе должна быть равна 100.
Сумма всех весов секций в исполнительном документе должна быть равна 100.
Рейтинг раздела — это рейтинг, который вы получаете для определенного раздела после того, как вы закончили его расчеты. Если рейтинг раздела представляет собой десятичное число, его необходимо сопоставить. Затем вы получите числовой рейтинг . Кроме того, на микроуровне у каждого предмета есть свой числовой рейтинг — числовой рейтинг предмета .
Десятичный балл — это балл, который вы получаете, разделив числовой рейтинг элемента на максимальный числовой рейтинг.
Взвешенная оценка — это балл, который вы получите, если умножите десятичный балл на вес.
Многие компании используют рейтинги производительности сотрудников, потому что эти рейтинги предоставляют количественные оценки. Кроме того, рейтинги сотрудников легко проводить, особенно при наличии калькулятора. Кроме того, поскольку система оценок одинакова для всех работников, эти оценки способствуют равенству на рабочем месте.
Если вам интересно, как измерить производительность сотрудников с помощью этого калькулятора, мы рассмотрим три разных раздела:
- Компетенции,
- цели производительности и
- Общий суммарный рейтинг.
Как рассчитать рейтинг сотрудников без взвешивания?
Организации могут выбирать, проводить ли проверку сотрудников с взвешиванием или без него. Если вы ищете простой и понятный подход к оценке, вам следует рассмотреть метод без взвешивания.
Более того, некоторые эксперты считают, что подсчет рейтинга сотрудников с взвешиванием слишком сложен и не так эффективен. Вместо этого они предлагают сократить количество целей и выбирать только важные модели поведения при оценке.
Вот основные шаги, которые необходимо предпринять при выполнении метода без взвешивания.
Усредненный метод без взвешивания – Компетенции
Если вы хотите оценить конкретные компетенции сотрудника, вы можете выбрать наиболее значимые из них, которые и будут вашими элементами контента. Вы можете выбрать любое качество, которое вы считаете чрезвычайно важным.
Вы можете выбрать любое качество, которое вы считаете чрезвычайно важным.
Например, если вы хотите проанализировать уровень производительности ваших сотрудников, вы должны включить «производительность» в качестве одной из компетенций. Если после оценок вы заметите, что эти уровни ниже допустимых, вам следует найти способы повысить производительность труда сотрудников на рабочем месте.
💡Скачать усредненный метод без взвешивания — Компетенции
Как видно из таблицы выше, мы составили список из шести компетенций. Максимальный числовой рейтинг для всех равен 5. Затем у нас есть числовой рейтинг элемента, который показывает, насколько успешен сотрудник в каждой области. В этом примере мы можем сказать, что у работника высокие оценки за продуктивность и пунктуальность и очень низкие оценки за посещаемость.
Чтобы получить десятичные баллы для этих полей, калькулятор автоматически делит числовой рейтинг элемента на максимальный числовой рейтинг:
4/5 = 0,8
5/5 = 1,0, и так далее.
Далее калькулятор суммирует общий десятичный балл по всем компетенциям:
0,8 + 1,0 + 0,6 + 0,8 + 1,0 + 0,4 = 4,6
Так как нужен рейтинг по всему разделу, калькулятор берет общий десятичный балл и делит его на общий максимальный десятичный балл. Общий максимальный десятичный балл равен количеству навыков/компетенций, которые вы добавили в калькулятор. В данном случае это 6,9.0006
4,6 / 6 = 0,76
После деления число умножается на максимальный числовой рейтинг.
0,76 x 5 = 3,8
Наконец, результатом является рейтинг раздела.
Теперь, если рейтинг раздела представляет собой десятичное число, вы должны сопоставить его, чтобы получить числовой рейтинг. Здесь 3,8, значит, будет 4. Рейтинг раздела для этой таблицы равен 4.
Метод усреднения без взвешивания – Цели производительности
Если вы хотите изучить цели производительности ваших сотрудников, вам нужно выбрать наиболее значимые цели. Эти цели должны быть жизненно важными для конкретной должности и согласовываться с целями компании.
Эти цели должны быть жизненно важными для конкретной должности и согласовываться с целями компании.
Например, при анализе работы торгового представителя важнейшими целями будут улучшение обслуживания клиентов, увеличение прибыли и постановка ежемесячных целей по продажам.
💡Скачать метод среднего без взвешивания – Цели производительности
Процесс расчета десятичного балла такой же, как и в предыдущем примере.
3 / 5 = 0,6
После того, как вы введете все числовые рейтинги элементов, калькулятор покажет вам все десятичные баллы и их сумму.
0,6 + 0,8 + 0,8 = 2,2
Также процесс расчета рейтинга раздела идентичен предыдущему. Поскольку здесь три гола, общий максимальный десятичный счет равен трем.
2,2 / 3 = 0,73
0,73 x 5 = 3,65 ≈ 3,7
Чтобы увидеть общий итоговый рейтинг, выполните простые расчеты. Калькулятор определяет средний числовой рейтинг для разделов, которые мы рассмотрели ранее.
Процесс расчета среднего числового рейтинга заключается в получении суммы рейтингов всех разделов. Затем эта сумма делится на количество разделов в исполнительном документе. Так, если бы в документе было четыре раздела, калькулятор разделил бы общее количество числовых оценок на четыре.
💡 Скачать общий суммарный рейтинг без взвешивания
В нашем случае числовые рейтинги по обоим разделам равны 4 и разделов два. Итак, общая оценка:
(4.0 + 4.0) / 2 = 4
Общий суммарный рейтинг равен 4.
Как рассчитать рейтинг сотрудников с учетом веса?
Расчет рейтинга сотрудников с учетом веса применяется в некоторых ситуациях. Например, когда компания считает, что определенные элементы производительности имеют решающее значение для сотрудников, работающих на одной и той же должности. Таким образом, в центре внимания оценки сотрудников находится оценка этих жизненно важных элементов. Таким образом, разделы получат свои веса, но также и элементы контента.
Например, если вы как работодатель хотите оценить работу всех менеджеров, элементы с более высоким весом будут иметь лидерство и командную работу. С другой стороны, если вы решите проанализировать агентов по продажам, более важными элементами будут обслуживание клиентов и общение.
Метод среднего с взвешиванием – Компетенции
При использовании метода с взвешиванием первым шагом является выбор наиболее важных компетенций, которыми должен обладать сотрудник. Следующий шаг такой же, как и для метода без взвешивания – добавление максимального числового рейтинга. Затем вы должны подумать о том, как сотрудник работает по сравнению с максимальным рейтингом. Вы добавите эти отзывы в столбец числового рейтинга товара.
💡 Скачать метод среднего с взвешиванием – Компетенции
Калькулятор автоматически измерит десятичный балл, разделив числовой рейтинг пункта на максимальный числовой рейтинг. Эти десятичные баллы идентичны баллам из предыдущего метода (расчет компетенций без взвешивания).
Как видно из приведенной выше таблицы, компетенции имеют собственный вес в зависимости от их важности. Сумма всех этих весов равна 100.
В нашем случае наиболее значимой компетенцией является общение с весом 30. А наименее важными являются посещаемость и пунктуальность. Говоря о посещаемости, если ваши сотрудники показывают низкие оценки в этой области, попробуйте установить правило учета рабочего времени сотрудников.
Рядом с весом находится столбец взвешенных баллов. Чтобы получить взвешенный балл, калькулятор умножает десятичный балл на вес:
0,8 x 30 = 24,0
1,0 х 25 = 25,0 и так далее.
Затем общий взвешенный балл автоматически представляется ниже:
24,0 + 25,0 + 9,0 + 12,0 + 5,0 + 4,0 = 79,0 общий максимальный взвешенный балл, который всегда равен 100,0.
79,0 / 100 = 0,79
Теперь нужно умножить десятичное число на максимальное числовое значение:
0,79 x 5 = 3,95
Рейтинг раздела равен 3,95, что означает, что он будет сопоставлен с 4.
Метод усреднения с взвешиванием – Цели производительности
Работодатели могут сделать акцент на определенных целях производительности при оценке сотрудников. . Это означает, что раздел «Цели эффективности» также будет иметь вес. Таким образом, каждый элемент контента (цель) тоже должен иметь свой вес.
💡Скачать метод среднего с взвешиванием – Цели производительности
Как и в методе без взвешивания, первым шагом будет оценка вашего сотрудника в каждой области и по каждой цели. Как только вы это сделаете, у вас будет готов столбец числового рейтинга элемента. Не забудьте также добавить максимальный числовой рейтинг.
Затем калькулятор разделит эти рейтинги на максимальный числовой рейтинг, чтобы получить десятичные баллы:
3 / 5 = 0,6 и так далее.
Теперь, когда у вас есть десятичные баллы, вам нужно определить вес для каждой цели в разделе. Сумма этих весов должна быть 100.
Затем калькулятор автоматически покажет вам взвешенный балл, умножив десятичный балл на его вес:
0,6 x 25 = 15,0 и так далее.
Кроме того, вы получите сумму взвешенных баллов:
15,0 + 36,0 + 24,0 = 75,0
Для расчета рейтинга раздела калькулятор делит взвешенный балл на общий максимальный взвешенный балл:
75,0 / 100 = 0,75
Кроме того, это десятичное число умножается на максимальный числовой рейтинг:
0,75 x 5 = 3,75
Рейтинг раздела равен 3,75, поэтому ему будет присвоено значение 4.
Общий суммарный рейтинг со взвешиванием
десятичные баллы по всем разделам. Итак, вам нужно ввести числовые рейтинги для взвешенных секций и максимальный числовой рейтинг. Калькулятор затем представит десятичный счет для обоих разделов. В нашем случае числовые рейтинги такие же, как и максимальный числовой рейтинг, поэтому расчет такой:
4 / 5 = 0,8
💡Скачать общий суммарный рейтинг с весами
Мы уже упоминали, что, помимо элементов контента, веса имеют и разделы. В этом случае Компетенция имеет более высокий вес (55), чем Цели эффективности (45). Итак, вам нужно добавить их веса в калькулятор. Таким образом, калькулятор умножит вес на десятичный балл раздела.
В этом случае Компетенция имеет более высокий вес (55), чем Цели эффективности (45). Итак, вам нужно добавить их веса в калькулятор. Таким образом, калькулятор умножит вес на десятичный балл раздела.
55 х 0,8 = 44,0
45 х 0,8 = 36,0
Сумма взвешенных баллов:
44,0 + 36,0 = 80,0
Наконец, калькулятор использует эту сумму, делит ее на общий балл (всегда 100), а затем умножает на максимальный числовой рейтинг:
80,0 / 100,0 = 0,8
0,8 x 5 = 4
Общий рейтинг равен 4. Как только вы введете все необходимые данные о сотруднике, такие как наиболее важные качества, которые вы хотите проанализировать, и оценки сотрудника по этим качествам, калькулятор сделает все остальное.
В этом калькуляторе есть две опции: расчет с взвешиванием или без него. Вы можете выбрать любую модель, которая лучше всего соответствует потребностям вашей компании. Итак, если вы хотите оценить определенные компетенции, вам следует использовать метод взвешивания.

 Рынок
Рынок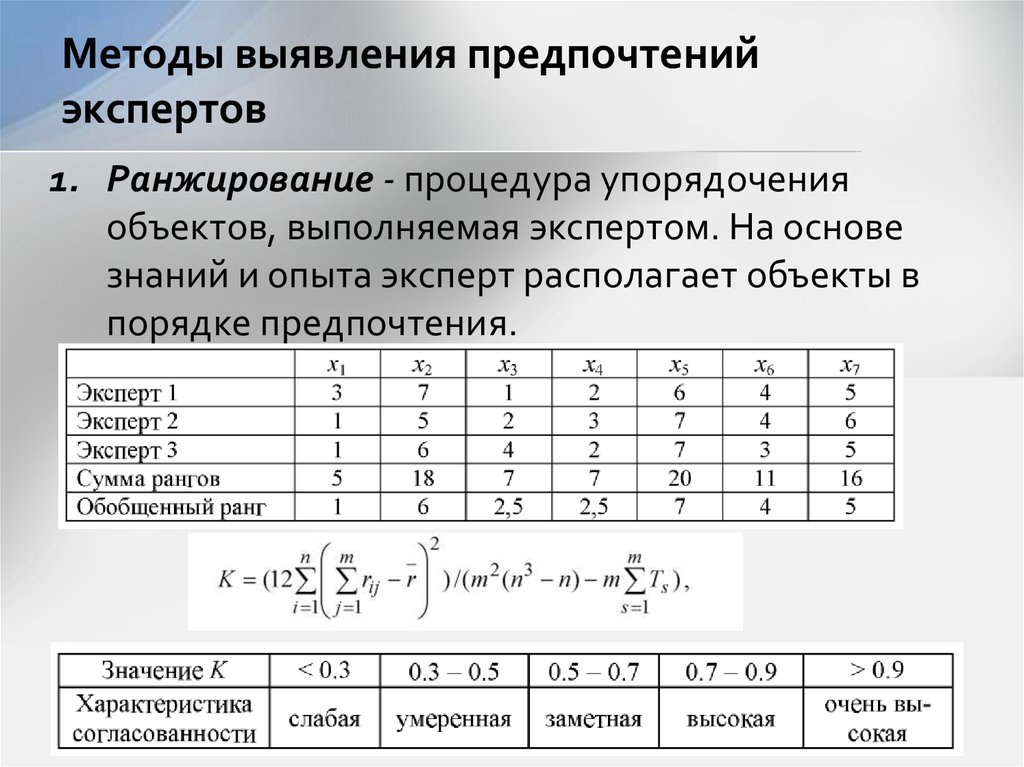


 ..
.. ..
.. ..
..