Формула ранжирования: 4.1. Правила ранжирования

4.1. Правила ранжирования

А. Ранжирование
качественных признаков

Пример 1.

Испытуемому
предлагается задание, в котором семь
личностных качеств необходимо упорядочить
(проранжировать) в двух столбцах: в левом
столбце в соответствии с особенностями
его «Я реального», а в правом столбце в
соответствии с особенностями его «Я
идеального». Результаты ранжирования
даны в таблице 2.

Таблица 2.

Я
реальное

Качества
личности

Я
идеальное

7

ответственность

1

1

общительность

5

3

настойчивость

7

2

энергичность

6

5

жизнерадостность

4

4

терпеливость

3

6

решительность

2

Б. Ранжирование
количественных признаков

Пример 2.

В результате
диагностики невроза у пяти испытуемых
по методике К.Хека и Х. Хесса были получены
следующие баллы: 24, 25, 37, 13, 12. Этому ряду
чисел можно проставить ранги двумя
способами:

  1. большему числу в
    ряду ставится больший ранг, в этом
    случае получится: 3, 4, 5, 2, 1;

  2. большему числу в
    ряду ставится меньший ранг: в этом
    случае получится: 3, 2, 1, 4, 5.

А. Формула для
подсчета суммы рангов по столбцу
(строчке)

Если
ранжируется N
чисел,
то сумма рангов расчитывается по формуле
(1.1):

1+2+3+…+N=N(N+1)/2

(1.1)

В
случае примера 1 число ранжируемых
признаков было равно N
=7,
поэтому сумма рангов, подсчитанная по
формуле (1.1), должна равняться 7(7+1)/2=28.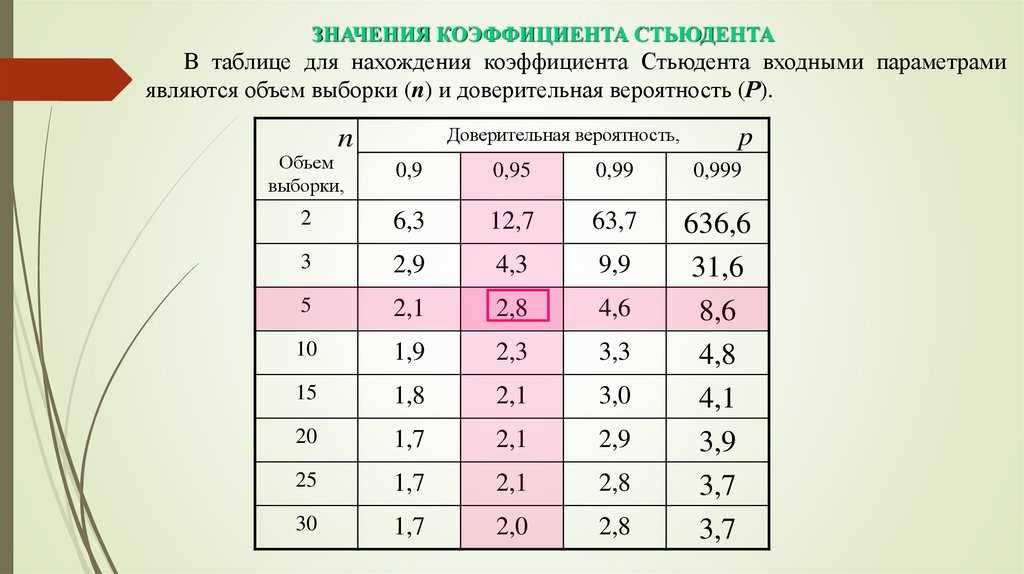

Сложим величины
рангов отдельно для левого и правого
столбца таблицы:

7 + 1 + 3+ 2 + 5 + 4 + 6 = 28
— для левого столбца и

1 + 5+ 7+ 6 + 4 + 3 + 2 = 28
— для правого столбца.

Суммы рангов
совпали.

Б.
Формула
для расчета суммы рангов в таблице

Ранжирование
по столбцам.

Пример
3. Результаты
тестирования двух групп испытуемых по
5 человек в каждой по методике
дифференциальной диагностики депрессивных
состояний В. А. Жмурова представлены в
таблице 3.

Таблица 3.

Номер
испытуемого

Группа
1

Группа
2

1

15

26

2

45

67

3

44

23

4

14

78

5

21

3

Задача: проранжировать
обе группы испытуемых как одну, т.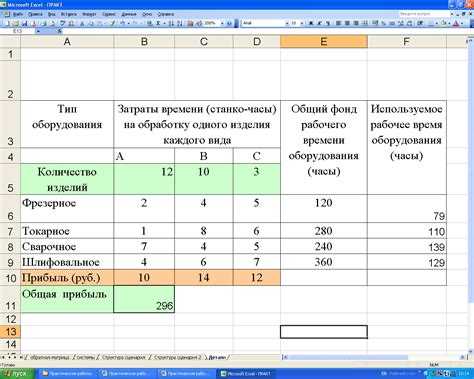  е.
объединить выборки и проставить ранги
объединенной выборке, сохраняя, однако
различие между группами. Сделаем это
в таблице 4, причем так, что максимальной
величине будем ставить минимальный
ранг.

Таблица 4.

Номер
испытеумого

Группа
1

Ранги

Группа
2

Ранги

1

15

8

26

5

2

45

3

67

2

3

44

4

23

6

4

14

9

78

1

5

21

7

3

10

Сумма

31

24

Поскольку у нас
получены суммы ранга по столбцам, то
общую сумму рангов можно получить,
сложив эти суммы: 31+24= 55.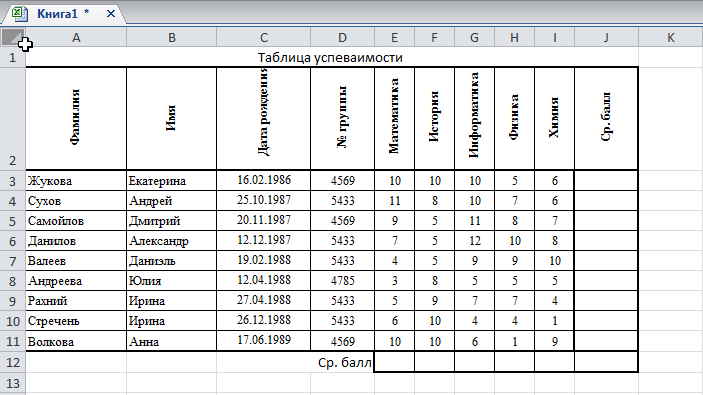

Чтобы применить
формулу (1.1), нужно подсчитать общее
количество испытуемых — это 5+5=10.

Тогда по формуле
(1.1) получаем: 10(10+1)/2=55.

Ранжирование
прведено правильно.

Если в таблице
имеется большое число строк и столбцов,
то можно использовать модификацию
формулы (1.1)

Сумма
рангов в таблице

=
(kc+1)kc/2
, (1.2)

где
k
— число строк, с — число столбцов.

Вычислим сумму
рангов по формуле (1.2.) для нашего примера.
В таблице 2 имеется 5 строк и 2 столбца,
сумма рангов = ((5·2+1)·5·2)/2=55

Ранжирование
по строкам

Пример 4.

В предыдущем
примере добавили еще одну группу
испытуемых 5 человек

.

Таблица 5. Проведем
ранжирование по строчкам.

Номер
испытуемого

Группа
1

Ранги

Группа
2

Ранги

Группа
3

Рагни

1

15

1

26

2

37

3

2

45

2

67

3

24

1

3

44

3

23

1

55

3

4

14

1

78

3

36

2

5

21

2

3

1

33

1

Суммы
по столбцам

8

10

12

В этой таблице
минимальному по величине числу ставится
минимальный ранг. Сумма рангов по каждой
строчке должна быть равна 6, поскольку
у нас ранжируется три величины: 1+2+3= 6. В
нашем случае так оно и есть. Теперь
просуммируем ранги по каждому столбцу
отдельно и сложим их.

Расчетная формула
общей суммы рангов для ранжирования по
строчкам для таблицы определяется по
формуле:

Сумма
рангов =
nc(c+1)/2,
(1.3.)

где
n
– количество испытуемых в столбце, с —
количество столбцов (групп).

Проверим правильность
ранжирования для нашего примера.

Реальная сумма
рангов в таблице 8+10+12= 30

По формуле (1.3):
5·3·(3+1)/2=30.

Следовательно,
ранжирование проведено правильно.

Случай одинаковых
рангов

Ранжирование
качественных признаков

А.
Ранжирование качественных признаков

Модифицируем
пример 1. и перепишем его в табл.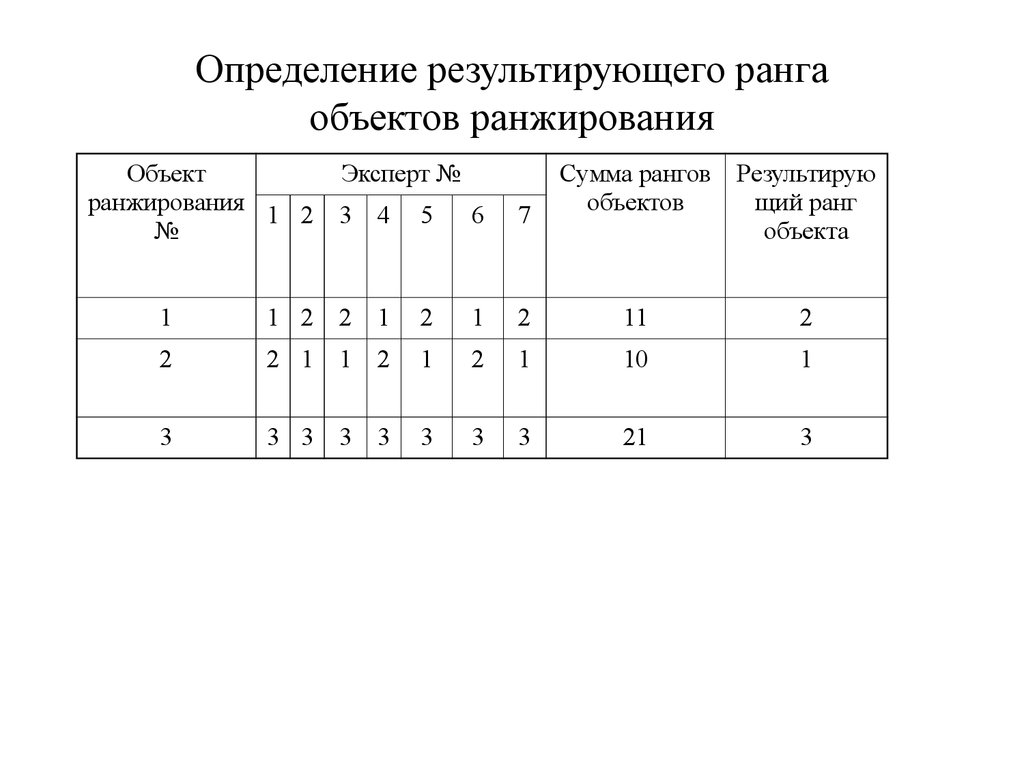 6.
Предположим, что при оценке особенностей
«Я реального» испытуемый считает, что
такие качества, как «настойчи­вость»
и «энергичность», должны иметь один и
тот же ранг. При проведении ранжирования
(столбец 1 табл. 6) этим качествам необходимо
проставить мысленные ранги (М.Р.), как
числа, обязательно идущие по порядку
друг за другом, и от­метить эти ранги
круглыми скобками — ( ). Однако посколь­ку
эти качества, по мнению испытуемого,
должны иметь одинаковые ранги, то во
втором столбце табл. 6, относяще­муся
к «Я реальному», следует поместить
среднее арифмети­ческое рангов,
проставленных в скобках, т.е. (2 + 3)/2 = 2,5.
Таким образом, второй столбец табл. 6 и
будет окончатель­ным итогом ранжирования
особенностей «Я реального», данным
испытуемым, а проставленные в этом
столбце ран­ги будут носить название
— реальные ранги (P.P.).

Аналогично при
ранжировании «Я идеального» испыту­емый
считает, что такие качества, как
«общительность», «энергичность» и
«жизнерадостность», должны иметь один
и тот же ранг. Тогда при проведении
ранжирования (см. столбец 5 табл. 6) этим
качествам необходимо проставить
мысленные ранги, как числа, обязательно
идущие по поряд­ку друг за другом, и
отметить эти ранги круглыми скобка­ми
— ( ). Однако поскольку эти качества, по
мнению испы­туемого, должны иметь
одинаковые ранги — то в четвертом
столбце табл. 6, относящемся к «Я
идеальному», следует поместить среднее
арифметическое рангов, проставленных
в скобках, т.е. (4 + 5 + 6)/3 = 5. Таким образом,
четвертый столбец таблицы 6 и будет
окончательным итогом ранжи­рования
особенностей «Я идеального», данным
испытуе­мым, а проставленные в этом
столбце ранги будут носить название —
реальные ранги. Подчеркнем еще раз, что
мыс­ленные (условные) ранги, как числа,
должны располагаться друг за другом по
порядку, несмотря на то что ранжируемые
качества в таблице данных не находятся
рядом друг с дру­гом.

Таблица 6.

Я
реальное

Качества
личности

Я
идеальное

М. Р.

P.P.

P.P.

М.Р.

7

7

Ответственность

1

1

1

1

Общительность

5

(4)

(2)

2,5

Настойчивость

7

7

(3)

2,5

Энергичность

5

(5)

5

5

Жизнерадостность

5

(6)

4

4

Терпеливость

3

3

6

6

Решительность

2

2

Обозначения:
М. Р.
— мысленные, или условные, ранги; P.P.
— ре­альные ранги.

Проверим
правильность ранжирования во втором
столб­це табл. 6, т.е. реальные ранги,
относящиеся к «Я реаль­ному»:

1
+ 2,5 + 2,5 + 5 + 4 + 6 = 28.

По формуле (1.1)
сумма рангов также равняется 28.
Сле­довательно, ранжирование проведено
правильно.

Проверим правильность
ранжирования в четвертом столбце табл.
6, т.е. реальные ранги, относящиеся к «Я
идеальному»:

1 + 2 + 3 + 5 + 5 + 5 + 7 =
28.

По формуле (1.1)
сумма рангов также равняется 28.
Сле­довательно, ранжирование проведено
правильно.

Б. Ранжирование
количественных характеристик (чисел)

Ранжирование чисел
рассмотрим на примере.

Пример.

Психолог получил у 11 испытуемых следующие
значения показателя невербального
интеллекта: 113,102,123,122, 117, 117, 102, 108, 114, 102,
104. Необходимо проранжировать эти
показатели, и лучше всего это сделать
в таблице 7.

Таблица 7

Номер
испытуемых

Показатели
интеллекта

Мысленные
ранги (М.Р.)

Реальные
ранги (P.P.)

1

113

6

6

2

102

(1)

2

3

123

11

11

4

122

10

10

5

117

[8]

8,5

6

117

[9]

8,5

7

102

(2)

2

8

108

5

5

9

114

7

7

10

102

(3)

2

11

104

4

4

В примере
встретились две группы из равных чисел
(102, 102 и 102; 117 и 117), поскольку числа в
группах раз­личны, то и скобки,
проставленные этим группам чисел, также
различны.

Проверим
правильность ранжирования по формуле
(1.1). Под­ставив исходные значения в
формулу, получим: 11·12/2 = 66. Суммируя
реальные ранги, получим:

6
+ 2 + 11 + 10 + 8,5 + 8,5 + 2 + 5 + 7 + 2 + 4 = 66.

Поскольку
суммы совпали, следовательно, ранжирование
про­ведено правильно.

Правила
ранжирования чисел таковы.

1.
Наименьшему (наибольшему) числовому
значению приписывается ранг 1.

2. Наибольшему
(наименьшему) числовому значению
приписывается ранг, равный количеству
ранжируемых ве­личин.

3. Одинаковым по
величине числам должны проставлять­ся
одинаковые ранги.

4. Если в ранжируемом
ряду несколько чисел оказались равными,
то им приписывается реальный ранг,
равный средней арифметической величине
тех рангов, которые эти числа получили
бы, если бы стояли по порядку друг за
дру­гом.

5. Если в ранжируемом
ряду имеется две и больше групп равных
между собой чисел, то для каждой такой
группы применяется правило 4, и мысленные
ранги каждой группы заключаются в разные
скобки.

6. Общая сумма
реальных рангов должна совпадать с
расчетной, определяемой по формуле
(1.1).

7. Не рекомендуется
ранжировать более чем 20 величин
(признаков, качеств, свойств и т.п.),
поскольку в этом слу­чае ранжирование
в целом оказывается малоустойчивым.

При необходимости
ранжирования достаточно большого числа
объектов следует объединять их по
какому-либо при­знаку в достаточно
однородные классы (группы), а затем уже
ранжировать полученные классы (группы).

Наиболее часто к
измерениям, полученным в ранговой шкале,
применяются коэффициенты корреляции
Спирмена и Кэндалла, и, кроме того,
используются разнообразные критерии
различий.

Основы ранжирования поисковых систем Яндекс и Google

Декабрь 19, 2017

Основы SEO

Алгоритмы

Основы ранжирования

Ранжирование — это процесс сортировки web-ресурсов в результатах поиска. Выполняется ранжирование согласно формуле: “чем больше значение суммы учитываемых факторов на сайте, тем лучше”.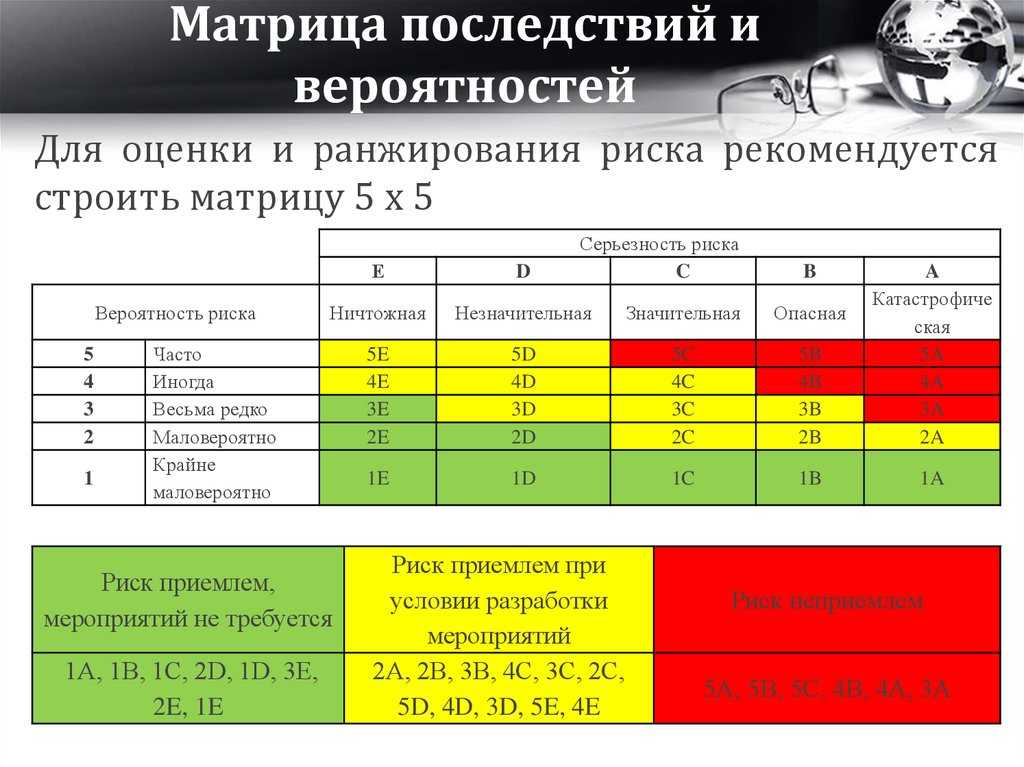 Факторы ранжирования могут быть и негативными — тогда они подставляются в формулу со знаком минус, то есть, уменьшают итоговую сумму, снижая позицию сайта в результатах поиска.

Формула ранжирования в приближенном виде выглядит следующим образом:

Y = F1(x1)*K1 + F2(x2)*K2 + F3(x3)*K3 + ...+ FN(xN)*KN

Y- итоговый ранк сайта — чем больше итоговая сумма, тем выше позиция в результатах поиска.

Ki– это весовой коэффициент (вес) этого фактора. Чем больше это значение, тем больше влияние фактора на позиции сайта.

FN (xN) — это некие функции (FN) от одного или нескольких факторов сайта, например, в качестве xN может быть % отказов, плотности ключевой фразы на странице и т. д.

Например, функция от количества вхождений ключевого слова в теге h2 (основной заголовок страницы) может выглядеть следующим образом:

Если ключевое слово в теге h2 встречается 1 раз, то функция вернёт единицу, если ключевой фразы не будет в h2 или она употребляется 2 раза и больше, то значение функции будет равно 0. Дробного количества вхождений ключевого слова быть не может — только целое число.

Далее значение этой функции умножается на весовой коэффициент данного фактора, например, на 0,008. В итоге, если ключевое слово будет присутствовать в теге h2, то, согласно нашим расчётам, это увеличит итоговое значение на 0,008.

Интерпретация формулы поискового ранжирования

Давайте запишем формулу в упрощенном виде: Y = A + B + C

  1. Формула позволяет сайту при недостатке одних характеристик выходить в ТОП результатов поиска за счёт других. Например, на сайте не хватает фактора С, но факторы A и B намного выше, чем у конкурентов. В этом случае сайт может оказаться в ТОП-10 даже выше, чем они. Поэтому очень качественные и интересные для пользователей тексты на качественном сайте (авторитетность сайта для Яндекс много значит) могут выводить его в ТОП даже при выходе за пределы рекомендованного диапазона по объему текста, плотности ключевых фраз и т. д.
  2. Также это означает, что в конкурентной сфере, когда показатели веб сайтов очень близки, недостаток значимого фактора невозможно компенсировать другим. Поэтому в конкурентных сферах исправление или улучшение какого-то одного или нескольких показателей не поможет выйти сайту в ТОП — надо заниматься всеми факторами. В первую очередь, теми, которые наиболее значимы для поисковых систем и по которым сильнее отставание от конкурентов.

Разнообразие результатов поисковой выдачи. Поисковые системы для обеспечения разнообразия в результатах поиска подмешивают в выдачу страницы, которые могут быть интересны отдельным группам пользователей по этому запросу. Например, в результатах поиска по запросу пользователя “Москва” могут появиться погода, билеты на перелет до Москвы, гостиницы, новости и т. д. Чем больше неопределённость в запросе, тем больше разнообразие в результатах.

Читать дальше подобные статьи

  • Как работают алгоритмы поиска
  • Факторы ранжирования сайтов, интернет магазинов поисковой системой Яндекс
  • Технология Яндекс «Спектр»
  • Что такое алгоритм «Многорукий бандит» Яндекса?

Online SEO-инструменты для продвижения сайтов

Проверьте свой сайт и сайты конкурентов на 205 факторов поисковых систем.

Восемь критериев ранжирования | Algolia

Восемь критериев ранжирования Algolia помогают определить, что релевантно как для текста, так и для бизнеса.

Опечатка

Алголия устойчива к опечаткам.

Критерий Typo в формуле ранжирования обеспечивает следующее ранжирование результатов поиска по запросам:

  1. Запросы без опечаток (точные совпадения)
  2. Запросы с одной опечаткой
  3. Запросы с двумя опечатками

Гео (если применимо)

Если вы используете функцию геопоиска, результаты ранжируются по расстоянию от ближайшего к самому дальнему.

Параметр aroundPrecision устанавливает точность ранжирования.

Words (если применимо)

Этот критерий применяется только в том случае, если вы используете необязательную настройку Words.

По умолчанию Algolia сопоставляет только те результаты, которые содержат всех слов запроса. С помощью optionalWords вы можете объявить некоторые слова необязательными. Критерий Words ранжирует их по количеству совпадающих слов, введенных пользователем ( , а не количество раз, которое слово встречается в записи).

Например, если пользователь ввел два слова, максимальное количество баллов по этому критерию равно 2, даже если запись содержит это слово 10 раз.

Фильтры

Если в запросе используются фильтры или необязательные фильтры, этот критерий ранжирует записи в соответствии с числом соответствующих фильтров , так что записи, не соответствующие фильтру, получают 0 баллов, а записи, соответствующие двум фильтрам, получают 2 балла.

Вы можете настроить подсчет очков с помощью:

  • Оценка фильтра, вы можете назначить разные оценки каждому фильтру.
  • Использование sumOrFiltersScores для накопления оценок дизъюнктивных совпадений (ИЛИ) для создания общей оценки .

Критерий «Фильтры» может быть полезен при определении релевантности, например, при продвижении результатов.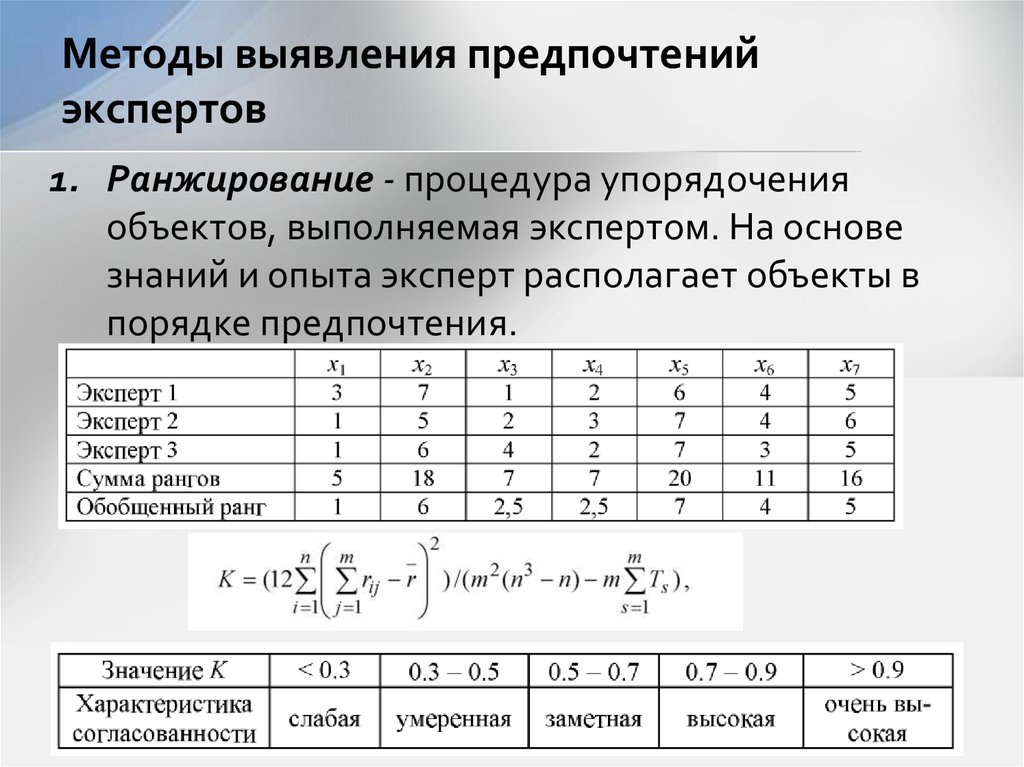

Близость

Для запроса с двумя или более словами Близость вычисляет, насколько близки эти слова друг к другу в соответствующей записи. Этот критерий отдает приоритет записям, в которых слова расположены ближе друг к другу.
Например, рассмотрим две записи со значением 9.0025 имя_актера атрибут: Джордж Клуни и Джордж Тимоти Клуни . Если пользователь ищет «Джордж Клуни», Джордж Клуни имеет лучшее расстояние близости (два слова запроса находятся на расстоянии 1 слова друг от друга) по сравнению с Джордж Тимоти Клуни (два слова запроса находятся на расстоянии 2 слова друг от друга).

Атрибут

Этот критерий учитывает только searchableAttributes : атрибуты в верхней части списка searchableAttributes имеют более высокий ранг, чем нижние.

Порядок совпадений внутри самого атрибута также важен. По умолчанию записи с совпадающими словами, расположенными ближе к началу данного атрибута, ранжируются выше.

Точно

Записи со словами, точно соответствующими условиям запроса, будут ранжироваться выше. Чем больше совпадающих слов в атрибуте записи, тем выше рейтинг этой записи. По умолчанию:

  • Точное совпадение — это когда полное слово в запросе без опечаток соответствует слову в атрибуте. Запросы из одного слова являются точными только в том случае, если они соответствуют атрибуту одного слова.
  • Неточное совпадение содержит опечатки или соответствует только префиксу.

Кроме того, совпадение синонимов и множественное/единственное число считаются точными. Таким образом, слово считается точным соответствием, если его синоним точно соответствует запросу.

Вы можете изменить настройки точного критерия.

Пользовательский

Этот критерий учитывает ваши пользовательские атрибуты ранжирования.

С несколькими пользовательскими атрибутами ранжирования поведение такое же, как и для других критериев: критерий используется только в том случае, если все предыдущие критерии совпадают.

Например, в следующем пользовательском рейтинге:

  1. Избранные записи ( избранные ) ранжируют записи со значением true выше, чем записи со значением false .
  2. Количество лайков ( number_of_likes ) ранжирует записи на основе этого числа: от самых до наименее понравившихся.

Комбинации атрибутов и близости

Когда в ранжировании появляется перед атрибутом, расчет ранжирования атрибута отличается от того, если появляется близость после атрибута . Это называется наиболее подходящим атрибутом .

Этот порядок представляет собой тонкое различие. Рекомендуется оставить ранжирование по умолчанию, поскольку близость обычно приводит к более точному определению наиболее подходящего атрибута.

Наиболее подходящий атрибут

Для определения наиболее подходящего атрибута Algolia использует два метода вычисления:

  • Ближайший по близости. Ранжирование основано на том, насколько близко два или более условия запроса друг к другу
  • Лучшая позиция. Считает слова в начале атрибута лучше , чем слова ближе к концу.

Формула ранжирования Algolia по умолчанию помещает Близость перед Атрибутом, что оказывает тонкое, но важное влияние на вычисление наиболее подходящего атрибута: атрибуты с совпавшими терминами ближайшими друг к другу будут иметь наивысший ранг.

Если вы поместите Близость после Атрибута или удалите критерий Близости, наиболее подходящими атрибутами будут те, чьи совпадающие термины находятся в лучшая позиция .

Пример

Например, рассмотрим индекс с двумя доступными для поиска атрибутами, профессия и полное имя , и следующие две записи:

 
  
  
 1
2
3
4
5
6
7
8
9
10
11
12
 
 [
  {
    "профессия": "Певец и комик",
    "полное имя": "Джерри Льюис",
    "ID объекта": "3"
  },
  {
    "profession": "Прирожденный певец",
    "полное имя": "Джерри Сингер",
    "ID объекта": "1"
  }
]
 
 Рассмотрим поисковый запрос «Джерри Сингер». Порядок формулы ранжирования по умолчанию:  Близость  до  Атрибут  *. В этом случае запись, содержащая два слова «джерри» и «певец» в непосредственной близости, ранжируется выше (независимо от порядка атрибутов). Для двух примеров записей:
  •   objectID  1 содержит слова запроса рядом в атрибуте полного имени
  •   objectID  3 имеет слова запроса в разных атрибутах.
 Поскольку у первого лучше показатель близости, он занимает первое место.
 Однако, если вы поместите  Близость  после  Атрибута  , ранжирование будет основано на  лучшей позиции  совпадающих терминов в доступных для поиска атрибутах ( профессия  и  полное имя  ). Следовательно, при запросе «певец Джерри» термин «певец» появляется в  профессия  перед  полным именем .
 Условное ранжирование в Excel с использованием функции СУММПРОИЗВ [RANKIF] 
 Главная / Формулы Excel /  Условное ранжирование в Excel с использованием функции СУММПРОИЗВ [RANKIF] 
 Условная формула для использования в качестве RANKIF
 Как работает эта формула условного RANKIF
 Часть 1: Сравнение имен
 Большая проверка 2 чем значения
 Часть 3. Умножение двух массивов
 Часть 4. Сложение + ОДИН
 Скачать образец файла
 Заключение
 Другие формулы . Вам будет интересно, почему в Excel нет функции условного ранжирования.
 Да никого нет.
 Теперь подумайте вот о чем: сталкивались ли вы когда-нибудь с ситуацией, когда вам нужно ранжировать значения, используя определенные критерии? И если да, то как решить эту проблему, ведь вы знаете, что в Excel нет функции RANKIF?
 Не уверены?
 Позвольте мне сказать вам кое-что: всякий раз, когда вы хотите создать условное ранжирование на основе определенного критерия или ранжирования по категориям, лучше всего использовать СУММПРОИЗВ. Да, вы правильно поняли, это СУММПРОДУКТ.
 Я влюблен в эту функцию последние пару лет, и сегодня в этом посте я покажу вам простой способ ранжирования значений с условием с помощью СУММПРОИЗВ. И это техника, которая может превратить вас из новичка в продвинутого пользователя Excel.
  Хотите узнать больше о SUMPRODUCT? 
 Начнем.
 В этом примере у нас есть список учеников с их баллами по разным предметам. Вы можете скачать этот образец файла отсюда, чтобы следовать ему.
 Здесь наша цель — ранжировать всех учащихся по каждому предмету. Это означает ранжирование учащихся от первого до последнего по каждому предмету, например, финансам, операциям и т. д., в соответствии с их оценками
 Условная формула для использования в качестве RANKIF 
  1.  Прежде всего, добавьте новый столбец в конце таблицу и назовите ее «Subject Wise Rank».
  2.  в ячейке D4 введите эту формулу =СУММПРОИЗВ((–(C2=$C$2:$C$121)),(–(B2<$B$2:$B$121)))+1 и нажмите Enter.
  3.  После этого примените эту формулу к концу столбца до последней ячейки.
  Поздравляем  , вы добавили предметные разряды для студентов, и вы думаете, что потратили несколько секунд?
 Разве это не просто и эффективно? Но важная часть состоит в том, чтобы понять, как работает эта формула.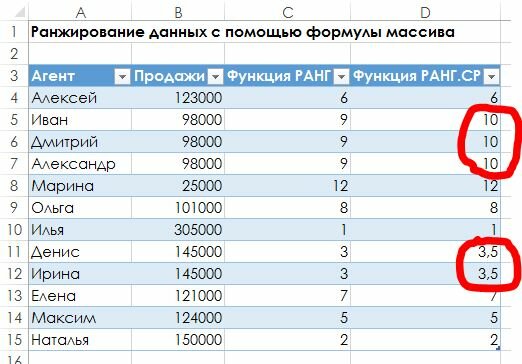 И поверьте мне, вы будете удивлены, когда узнаете, что вы сотворили здесь чудо с помощью этой функции.
 Как работает эта условная формула RANKIF 
 Чтобы понять это, нам нужно разбить эту формулу на три части. И, пожалуйста, помните, что СУММПРОИЗВ — это функция, которая может принимать массивы, даже если вы не применили формулу как массив.
 Часть 1: Сравнение имен 
 В первой части вы использовали  (–(C2=$C$2:$C$121))  для сравнения имени субъекта со всем диапазоном. И он вернет массив, в котором все эти значения будут истинными и совпадут с названием темы «Финансы».
 Чтобы проверить, просто отредактируйте свои формулы в ячейке D4, выберите только первую часть формулы и нажмите F9. Он покажет все значения массива.
 Здесь все значения, совпадающие с именем субъекта из ячейки D4, являются ИСТИННЫМИ, а остальные — ЛОЖНЫМИ. Итак, дело в том, что он вернул TRUE во всем массиве, где совпадает имя субъекта.
 И, наконец, вы должны использовать двойной знак минус  , чтобы преобразовать ИСТИНА и ЛОЖЬ в 1 и 0.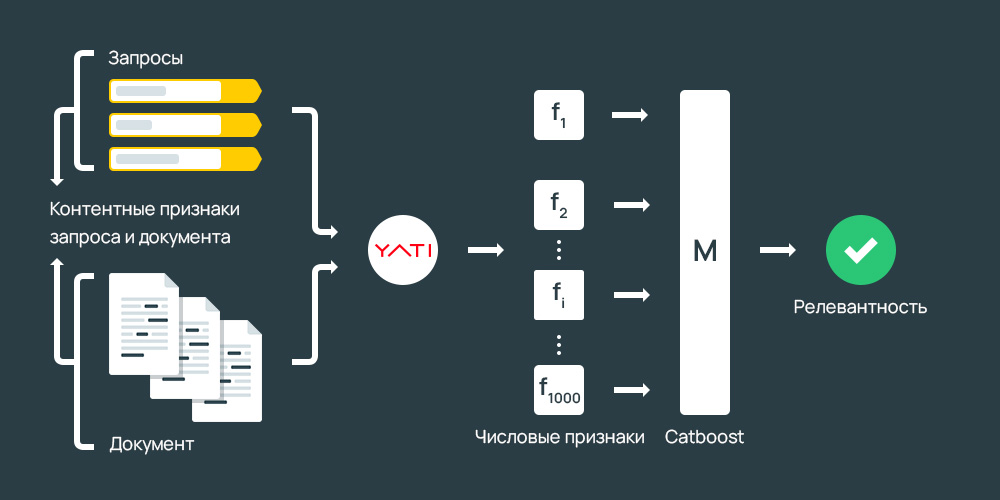 предмет не соответствует.
 Часть 2: проверка значений, превышающих значения 
 Во второй части   вы использовали  (--(B2<$B$2:$B$121)) , чтобы проверить оценки других учащихся, превышающие оценку Тамеки. . И он возвращает массив, в котором все значения ИСТИНА, где оценки больше, чем Тамека.
 Чтобы проверить, просто отредактируйте формулы в ячейке D4, выберите только вторую часть формулы и нажмите F9. Он покажет все значения массива.
 Здесь все значения, превышающие «24», являются ИСТИННЫМИ, а остальные — ЛОЖНЫМИ. Итак, дело в том, что он вернул ИСТИНА во всем массиве, где оценки больше «24».
 И, наконец, вы должны использовать двойной знак минус, чтобы преобразовать ИСТИНА и ЛОЖЬ в 1 и 0. Теперь это будет выглядеть так.
 Результат этой части формулы: У нас есть 1, если оценка больше, и 0 баллов, если оценка равна или ниже.
 Часть 3. Умножение двух массивов 
 Теперь сделайте глубокий вдох и расслабьтесь.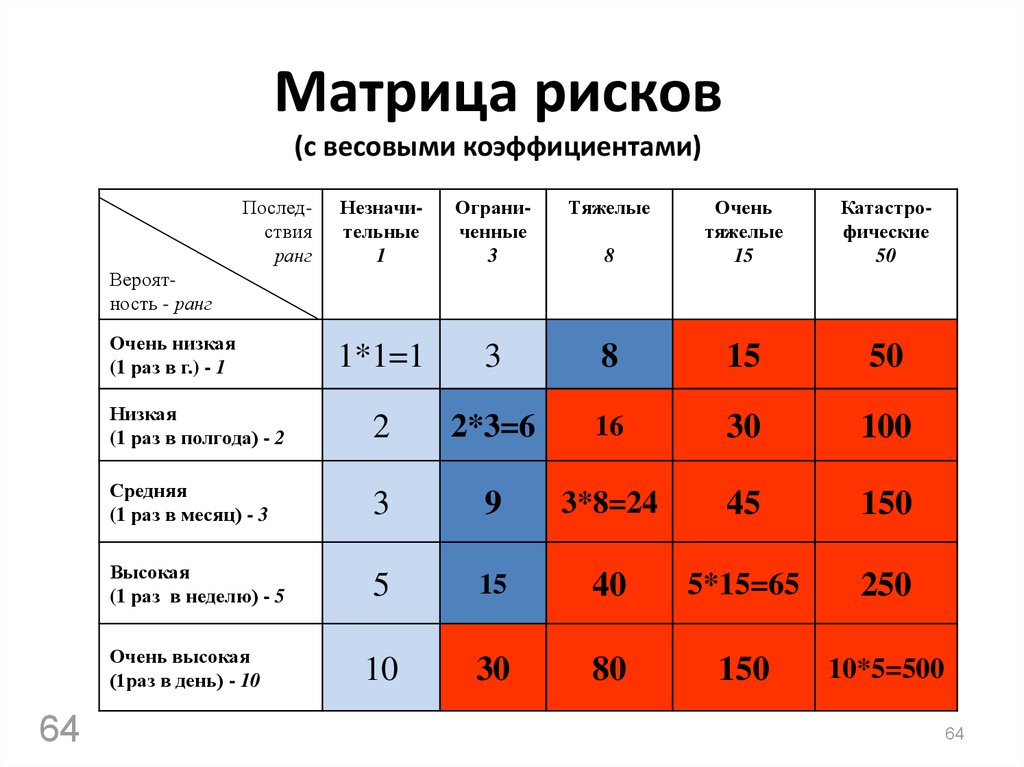 Замедлите свой ум и думайте так. На данный момент у нас есть два разных массива.
  1.  В первом массиве у вас есть 1 для всех значений, где тема совпадает, и 0, если нет совпадения.
  2.  Во втором массиве у вас есть единица для всех значений, при которых оценка учащихся выше, и ноль, если она равна или ниже.
 Теперь, когда СУММПРОИЗВ умножает эти два массива, вы получите 1 только для тех учеников, чей предмет совпадает, и оценка больше, чем Тамека.
 Только взгляните на это, есть еще 9 студентов с более высокими оценками, чем у Тамеки по финансам.
 Часть 4: Добавление + ЕДИНИЦА 
 Если вам интересно узнать, почему вам нужно добавить 1 в итоговую формулу, то вот причина этого: На данный момент вы знаете, что всего 9есть ученики, чьи оценки выше, чем у Тамеки. Итак, если там 9 учеников, Тамека должен быть на 10-м месте.
 Вот почему вам нужно добавить 1 в конце формулы.
 Загрузить образец файла 
 Заключение 
 Если вы спросите меня, я считаю, что СУММПРОИЗВ — одна из самых мощных функций в библиотеке Excel, а метод, который мы использовали выше, прост и эффективен.