Содержание
НОУ ИНТУИТ | Лекция | Генетические алгоритмы многокритериальной оптимизации
< Лекция 4 || Лекция 5: 123456 || Лекция 6 >
Аннотация: В большинстве реальных практических задач, как правило, необходимо выполнить оптимизацию по нескольким критериям. Многокритериальная оптимизация основана на поиске решения, которое одновременно оптимизирует не одну, а несколько функций. В этой лекции изложены основы многокритериальных ГА на основе концепции Парето. Описана общая структура многокритериального ГА и различные обобщения ГА для многокритериальной оптимизациии, включая: векторную оценку, ранжирование по Парето, метод взвешенной функции со случайными и адаптивными весами. Рассмотрены методы оценки качества решений в случае многокритериальной оптимизации.
Ключевые слова: оптимизация, пространство, интерпретация, вектор, многокритериальная оптимизация, поиск, пользователь, множества, доминируемые и недоминированные решения, концепция парето, многокритериальные генетические алгоритмы, операторы, хромосомы, цикла, информация, вероятность, векторная оценка, мощность, длина, ранг, ранжирование, sorting, genetic, algorithm, значение, вес, отношение, равенство, расстояние
intuit.ru/2010/edi»>Оптимизация по нескольким критериям требует применения специальных методов, которые существенно отличаются от стандартной техники, ориентированной на оптимизацию одной функции.Без потери общности задачу многокритериальной оптимизации можно сформулировать следующим образом:
Здесь пространство поиска решений определяется следующим образом
В случае многокритериальной оптимизации иногда используется графическая интерпретация как пространстве поиска решений , так и пространстве критериев
где — вектор значений целевых функций. Другими словами является множеством образов в .
5.1. Концепция доминирования Парето
Следует отметить, что многокритериальные задачи принципиально отличаются от однокритериальных. В последнем случае мы пытаемся найти решение, которое лучше всех остальных решений. В случае многокритериальной оптимизации необязательно существует решение, которое является лучшим относительно всех критериев вследствие возможных конфликтов. Решение может быть лучшим относительно одного критерия и худшим относительно других критериев.
В случае многокритериальной оптимизации необязательно существует решение, которое является лучшим относительно всех критериев вследствие возможных конфликтов. Решение может быть лучшим относительно одного критерия и худшим относительно других критериев.
Поэтому при многокритериальной оптимизации выполняется поиск не одной особи, а множество хромосом, оптимальных в смысле Парето [1,2,3]. Обычно пользователь имеет возможность выбирать оптимальное решение из этого множества.
Для этих целей удобно классифицировать потенциальные решения многокритериальной проблемы на доминируемые и недоминируемые решения. Решение называется доминируемым, если существует решение , не хуже чем по всем критериям, то есть для всех оптимизируемых функций :
для всех при максимизации функции и
для всех при минимизации функции .
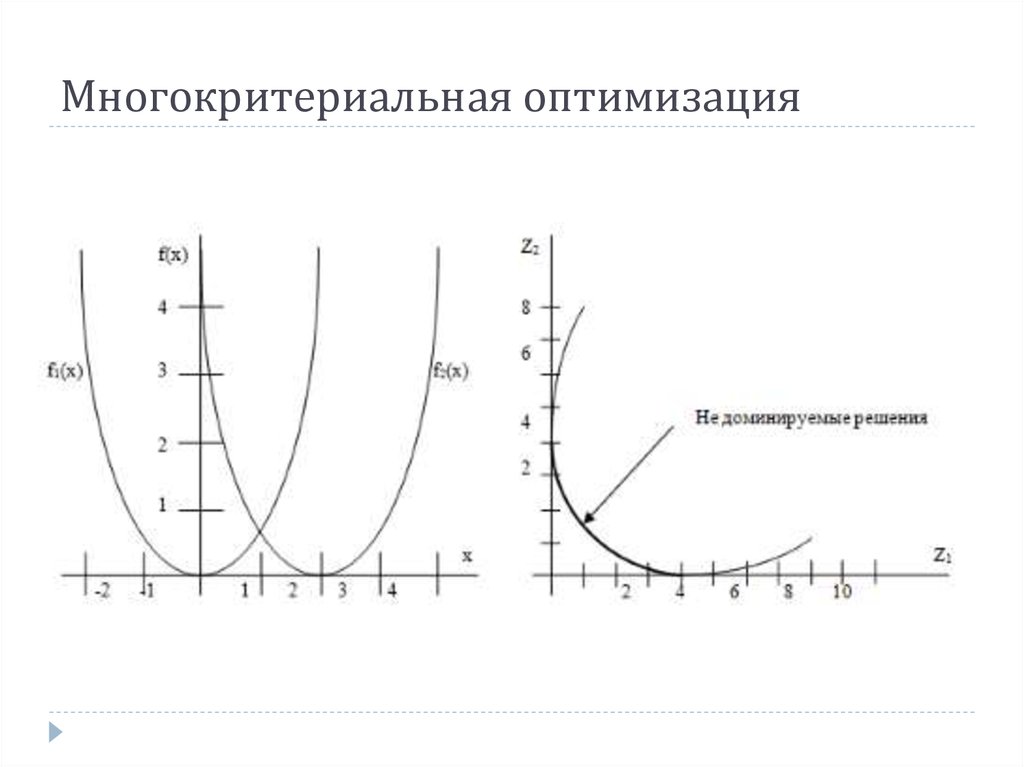
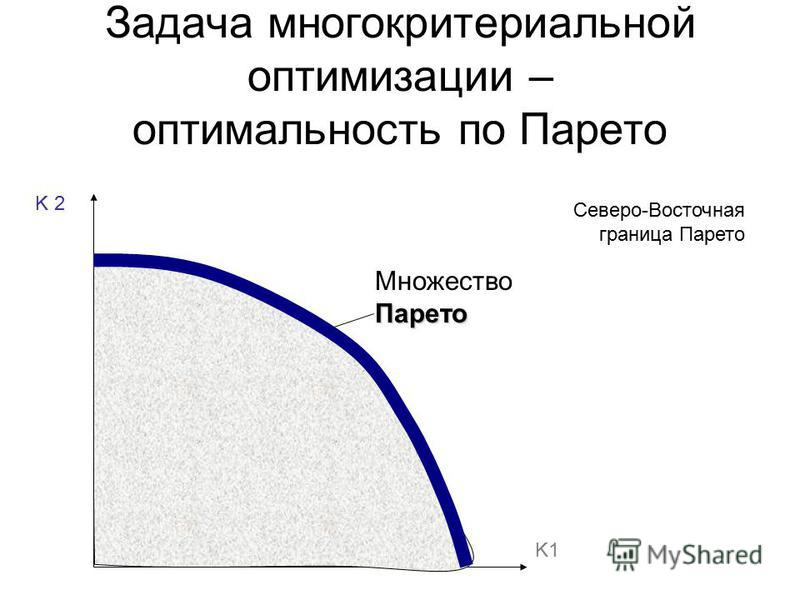
Если решение не доминируемо никаким другим решением, то оно называется недоминируемым или оптимальным в смысле Парето. Концепция Парето оптимальных решений представлена на рис.5.1, где в пространстве критериев квадратики соответствуют Парето оптимальным решениям, а ромбики – неоптимальным. При этом точка в пространстве поиска решений является действенной (эффективной), если и только если ее образ в является не доминируемым.
Присущие ГА свойства способствуют их эффективному применению при решении задач многокритериальной оптимизации, поскольку ГА основаны на использовании множества потенциальных решений — популяции и глобальном поиске в нескольких направлениях. Напомним, что ГА не предъявляют никаких требований к виду целевых функций и ограничениям.
Рис.
5.1.
Концепция Парето оптимальных решений
Фактически ГА относится к методам мета-стратегии. При применении ГА для решения конкретной задачи необходимо выбрать или разработать основные компоненты, такие как метод кодирования потенциального решения, генетические операторы кроссинговера и мутации, метод отбора родителей, построить фитнесс-функцию, позволяющую оценивать потенциальные решения и т.д.
Поскольку многокритериальная оптимизация является естественным развитием обычной численной или комбинаторной оптимизации, то многие разработанные методы были распространены на этот более общий случай. При использовании ГА для многокритериальной оптимизации центральным вопросом является построение фитнесс-функции. За последние десятилетия, следуя [2], разработано несколько подходов, которые можно разделить на представленные ниже три поколения:
- intuit.ru/2010/edi»>Поколение 1. Векторная оценка (vector evaluated -veGA) [5].
- Поколение 2. Ранжирование по Парето + Разнообразие:Многокритериальный ГА (multiobjective GA — moGA) [6].
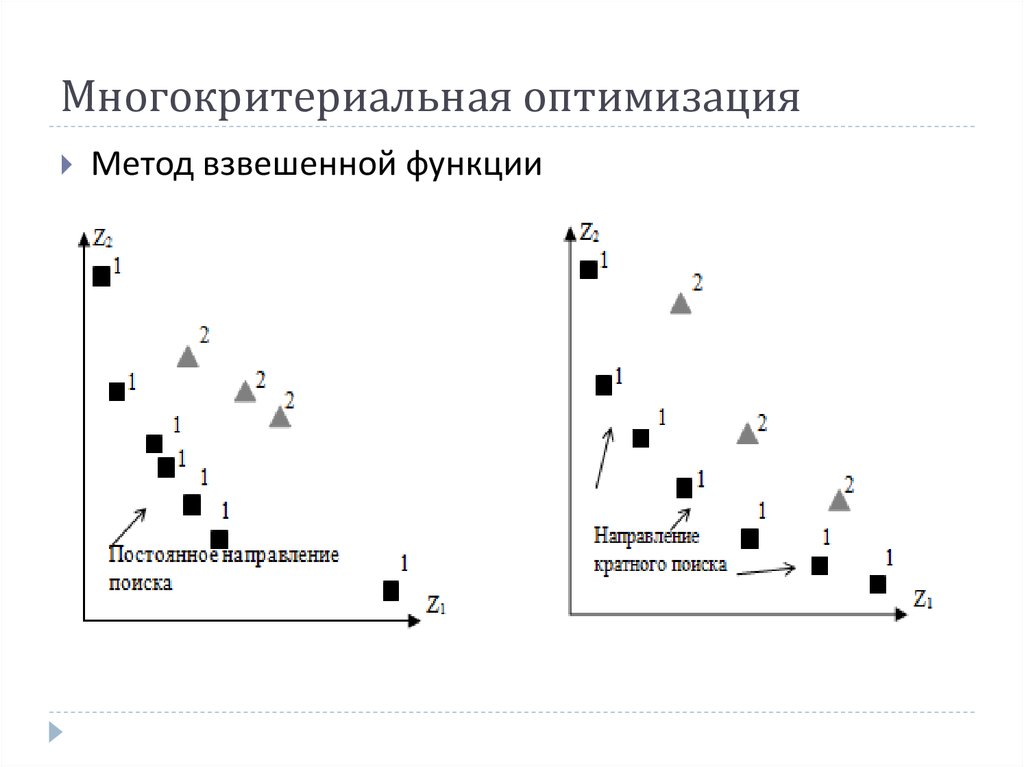
- Поколение 3. Взвешенная сумма + Элитизм:Случайный взвешенный ГА (rwGA) [7]; Адаптивный взвешенный ГА (awGA)[8]; Недоминируемый ГА на основе сортировки (nsGA) [9]; Интерактивный ГА с адаптивными весами (i-awGA) [10].
Далее мы рассмотрим эти методы более подробно.
Дальше >>
< Лекция 4 || Лекция 5: 123456 || Лекция 6 >
МВ КМА | Методы многокритериальной оптимизации
- Краткая справка
- Проекты
- Основные публикации
- Демонстрация
основных методов оптимизации
Новая система лицензирования
Разработана система управления лицензиями на систему СВИРЬ-Р через Интернет.
Далее… »
Вышли в свет
С.В.
Микони
Учебное пособие Теория принятия управленческих решений – СПб.: Издательство «Лань», 2015. – 448 с.: ил.
В учебном пособии большое внимание уделено изучению свойств матрицы парных сравнений,
как модели, непосредственно связывающей предпочтения ЛПР и приоритеты сущностей.
Изложение изучаемых моделей и методов выбора основывается на формальной модели критерия.
Критерии разделены на две группы: превосходства и соответствия. Методы выбора разделены
на методы критериального и функционального выбора, причем все функции рассматриваются
с позиции полезности.
Далее… »
Получен грант РФФИ
Грант
РФФИ № 17-01-00139
«Разработка методологии структурирования и анализа свойств сложных технических систем»
Проект направлен на разработку научно-методических основ оценивания сложных технических систем. В результате выполнения проекта должен повыситься уровень обоснованности и качества иерархических моделей сложных технических систем (СТС) различного назначения
В результате выполнения проекта должен повыситься уровень обоснованности и качества иерархических моделей сложных технических систем (СТС) различного назначения
Далее… »
Консультации по проектирования систем многомерного оценивания объектов любой природы.
Решение задач многомерного оценивания объектов в системе СВИРЬ.
Далее… »
Использование методов многокритериальной оптимизации
Методы многокритериальной оптимизации используются для решения
следующих задач выбора:
- Отбор допустимых объектов
- Упорядочение всех объектов относительно общей цели
- Упорядочение допустимых объектов относительно общей цели
(условная оптимизация) - Упорядочение объектов относительно индивидуальных целей
- Упорядочение объектов по образцу
- Нахождение наилучшего (среднего, наихудшего) объекта
Различают 2 группы методов многокритериальной
оптимизации на конечном множестве альтернатив: векторные
и скалярные. Под векторной оптимизацией
Под векторной оптимизацией
на конечном множестве объектов понимается нахождение варианта
(альтернативы) с наилучшим значением векторного критерия.
Наибольшее распространение получили следующие методы векторной
оптимизации:
- Оптимизация по Парето;
- Лексиминная оптимизация;
- Оптимизация по приоритету критериев
(лексикографическая оптимизация).
Под скалярной оптимизацией на конечном множестве
объектов понимается нахождение варианта (альтернативы)
с наилучшим значением скалярного критерия. Скалярные оценки
объектов вычисляются путём преобразования векторного аргумента
в скаляр. Наибольшее распространение получили функции,
усредняющие значения признаков (аддитивная
и мультипликативные) или их разброс (минимаксная
и максиминная). Они называются обобщающими (синтезирующими).
При задании обобщающей функции (ОФ) важная роль отводится
выбору шкал признаков и их весовым коэффициентам. Наверх
Наверх
Публикации
| № | Наименование
работы | Вид работы | Издательство,
журнал, номер, год | Стр. | Фамилии авторов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Сопоставление расстановок мест объектов
в порядковых шкалах | Доклад | Труды междунар. конф. по мягким вычислениям
и измерениям. SCM’2000, -СПб.: СПбГЭТУ, 2000, Том 1 | с. 58-60 | Микони С. В. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | Выбор и упорядочение объектов
с иерархической системой показателей | Доклад | Труды междунар. конф. по мягким вычислениям
и измерениям.  SCM’2000, -СПб.: СПбГЭТУ, 2000, Том 1 SCM’2000, -СПб.: СПбГЭТУ, 2000, Том 1 | с. 54-57 | Микони С. В., Козченко Р. В.,
Созоновский П. Г. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | Методы мягкого выбора | Доклад | Труды конф. КИИ-2000, -М.: Изд-физ.мат.лит-ры, 2000,
том 2 | с. 472-479 | Микони С. В. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | Многокритериальная оценка объектов в системе
СВИРЬ | Доклад | Труды конф.IEEE AIS’02 и CAD-2002,
Дивноморское, 5-10.09. 2002, -М: Наука. Физматлит, 2002 | с. 382-387 | Микони С. В. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | Конструирование методов выбора и ранжирования
на основе функционального базиса | Доклад | Сборник докладов междунар.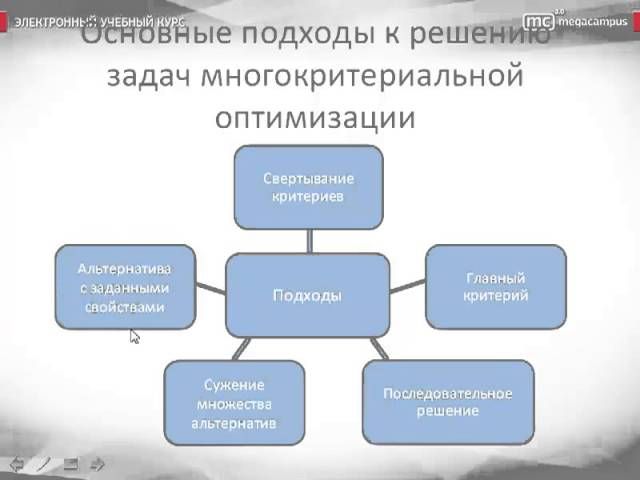 конф. по мягким конф. по мягким
вычислениям и измерениям SCM’2003, -СПб.: 25-27 июня 2003, СПбГЭТУ, том 1 | с. 119-122. | Микони С. В., Сорокина М. И. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | Оценка деятельности кафедр университета как задача
рационального выбора | Доклад | Вестник ПГУПС, — СПб.: ПГУПС, 2003,
Вып.1 | с. 124-130 | Микони С. В. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | Парадоксы многокритериального ранжирования объектов | Доклад | Сборник докладов междунар. конф. по мягким
вычислениям и измерениям SCM’2003, -СПб.: | с. 25-27 | Микони С. В., Бураков Д. П. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | Оценка деятельности кафедр университета как задача
рационального выбора | Доклад | Вестник ПГУПС, -СПб. : ПГУПС, 2003, Вып.1 : ПГУПС, 2003, Вып.1 | с.124-130. | Микони С. В. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | Систематизация задач рационального выбора | Доклад | Труды конф.IEEE AIS’03 и CAD-2003,
Дивноморское, 3-10.09. 2003, -М: Наука. Физматлит, 2003 | с. 428-433 | Микони С. В. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | Определение приоритета критериев
в иерархическом пространстве | Доклад | Вестник Томского гос. ун-та, Приложение. Материалы
научных конференций, симпозиумов, школ, проводимых в ТГУ, № 9 (II), август 2004 | с. 48-52 | Микони С. В., Бураков Д. П. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | Определение весовых коэффициентов функции полезности
при оценивании деятельности кафедр университета | Доклад | Вестник ПГУПС, -СПб. : ПГУПС, 2004, Вып.2 : ПГУПС, 2004, Вып.2 | с.137-143 | Микони С. В., Ледяев А. П., Якубчик
П. П. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | Два способа учёта зависимости критериев при решении
рейтинговых задач | Доклад | Труды конф. IEEE AIS’05 и CAD-2005,
Дивноморское, 3-10.09. 2005, -М: Наука. Физматлит, 2005 | с. 318-327 | Микони С. В., Бураков Д. П. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | Решение рейтинговых задач в системе СВИРЬ | Доклад | Открытое образование
N 4 (51) 2005 | с. 41-46 | Ледяев А. П., Микони С. В., Якубчик
П. П., Бураков Д. П. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | Решение задач ВАР численными методами | Доклад | Труды конф.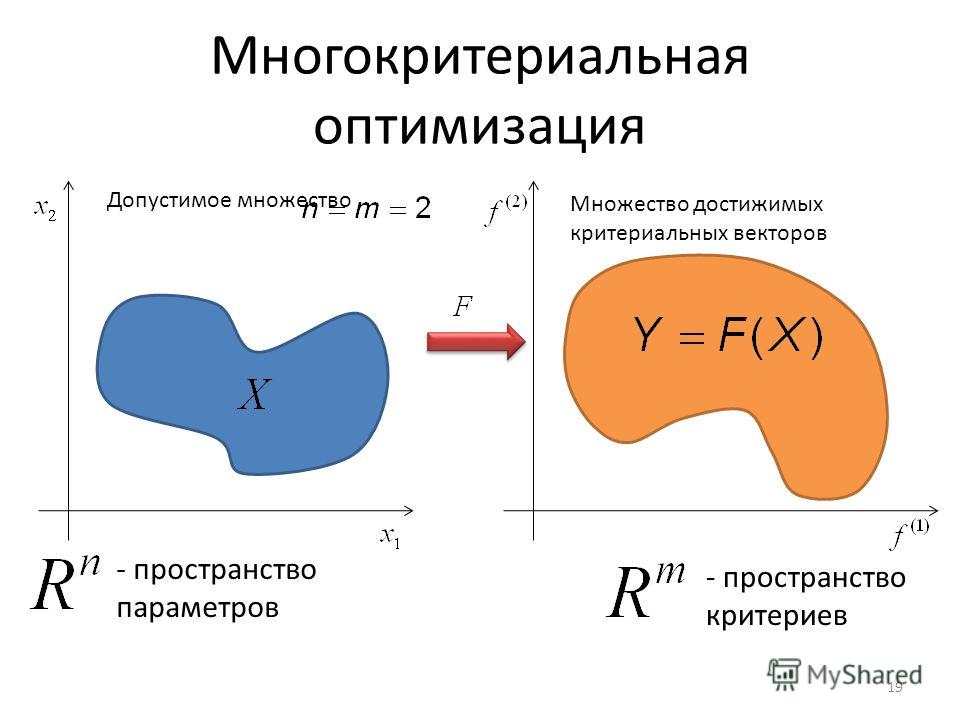 IEEE AIS’06 и CAD-2006, IEEE AIS’06 и CAD-2006,
Дивноморское, 3-10.09. 2006, -М: Наука. Физматлит, 2006 | с 171-176 | Микони С. В., Бураков Д. П. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | Проверка результатов многокритериального упорядочения
на Парето-оптимальность | Доклад | Известия ПГУПС — СПб.: ПГУПС,
2006 — Вып. 2(7). | с. 28-34 | Бураков Д. П. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | Стохастический способ ортогонализации пространства
критериальных функций при решении рейтинговых задач | Доклад | Известия ВУЗов. Приборостроение. 2006,
Т. 49, № 12 | с. 3-7 | Бураков Д. П. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17 | Определение рейтинга подразделений железной дороги
по итогам выполнения планов | Доклад | Труды X-й СПб. конференции «Региональная конференции «Региональная
информатика-2004»,24-26.10.2006, -СПб.: СПОИСУ, 2006 | с. 266-273 | Микони С. В., Тихомиров В. О.,
Тришанков В. В., Сорокина М. И. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | Экспериментальное исследование процедуры
ортогонализации пространства критериальных функций | Доклад | Известия ВУЗов. Приборостроение. 2007,
Т. 50, № 3 | с. 3-7 | Бураков Д. П. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | Вклад признака в общую оценку объекта при
использовании произвольных функций полезности | Доклад | Известия ПГУПС — СПб.: ПГУПС,
2006 — Вып. 3(8) | — | Сорокина М. И. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | Обобщенная модель задач многокритериальной оптимизации
и идентификации | Доклад | Труды междунар. конф. по мягким вычислениям конф. по мягким вычислениям
и измерениям SCM’2007, Том 1, СПб.: — СПбГЭТУ, 2007 | с. 243-249 | Микони С. В., Бураков Д. П.,
Сорокина М. И. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21 | Определение согласованности групповой экспертизы
на шкале качества | Доклад | Труды междунар. конф. по мягким вычислениям
и измерениям SCM’2007, Том 1, СПб.: — СПбГЭТУ, 2007 | с. 97-101 | Микони С. В., Сорокина М. И. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22 | Определение рейтинга подразделений по итогам
выполнения планов | Доклад | Труды конф.IEEE AIS’07 и CAD-2007,
Дивноморское, 3-10.09. 2007, -М: Наука. Физматлит, 2007 | с. 335-340 | Микони С. В. Наверх Наверх
pymoo: Многоцелевая оптимизация в PythonОбзор На что обратить внимание в pymoo 0.6.0 .
Наслаждайтесь нашим новым релизом! Наша структура предлагает современные одно- и многоцелевые алгоритмы оптимизации и множество pip установить -U pymoo Обратите внимание, что некоторые модули могут быть скомпилированы для ускорения вычислений (опционально). Команда Руководство по началу работы: Наиболее важные шаги в многоцелевом Информационный бюллетень: Подпишитесь на нашу рассылку, чтобы быть в курсе последних событий Discord: Присоединяйтесь к нашему серверу Discord, чтобы получить помощь или обсудить оптимизацию в контексте нашего фреймворка. ОсобенностиКроме того, наша структура предлагает множество различных функций, которые охватывают различные аспекты многоцелевой оптимизации: Интерфейс Функция: Свернуть Параметры: Проблема, Дополнительно: Обратный вызов, Возвращает: Результат Связанный: Спроси и расскажи, Проблемы Одноцелевые: Экли, Многоцелевой: BNH, Многоцелевой: ДТЛЗ, Ограничено: Динамический: DF Связанный: Определение проблемы, Алгоритмы Одноцелевой: GA, Многоцелевой: NSGA-II, Многоцелевой: NSGA-III, Связанный: Справочные направления, Настройка Типы переменных: Двоичные, Примеры: Предвзятая инициализация, Операторы Выборка: Выбор: Кроссовер: Мутация: Ремонт Визуализация Точечная диаграмма (2D/3D/ND), Многокритериальное принятие решений Компромиссное программирование, Индикатор производительности ГД, Разложение Взвешенная сумма, Тематические исследования Выбор подмножества, Список алгоритмов
Cite UsЕсли вы использовали нашу структуру в исследовательских целях, вы можете ссылаться на нашу публикацию: J. Blank and K. Deb, pymoo: Multi-Objective Optimization in Python, in IEEE Access, vol. 8, стр. 89497-89509, 2020, doi: 10.1109/ACCESS.2020.29 BibTex: @ARTICLE{pymoo,
автор={Дж. {Пробел} и К. {Деб}},
журнал={Доступ IEEE},
title={pymoo: многоцелевая оптимизация в Python},
год = {2020},
объем = {8},
число = {},
страницы={89497-89509},
}
Новости 11 июля 2022 г. 12 сентября 2021 г.: Спустя некоторое время стала доступна более крупная версия pymoo (версия 0.5.0 ). 4 сентября 2020 г.: Мы более чем рады сообщить, что доступна новая версия pymoo (версия 0.4.2 ). Эта версия Другие новости О Эта структура основана на anyoptimization, исследовательском сообществе Python. Он разработан и поддерживается Джулианом Бланком, членом Мы разработали основу для исследовательских целей и надеемся внести свой вклад в область исследований, предоставив инструменты Если вы собираетесь использовать нашу платформу для любые целей получения прибыли, пожалуйста, свяжитесь с нами. Также имейте в виду, что даже Кроме того, любой вклад более чем приветствуется: (i) Дайте нам на GitHub. (ii) Чтобы предлагать все больше и больше новых алгоритмов и функций, мы будем более чем рады, если кто-то захочет внести свой вклад в разработку кода. Вы можете видеть это как (iii) Вам нравится наша структура, и вы хотели бы использовать ее для получения прибыли? Если вы обнаружите ошибку или у вас есть какие-либо опасения относительно правильности, пожалуйста, используйте Контент
[PDF] МНОГОЦЕЛЕВАЯ ОПТИМИЗАЦИЯ: ИСТОРИЯ И ПЕРСПЕКТИВЫ
title={МНОГОЦЕЛЕВАЯ ОПТИМИЗАЦИЯ: ИСТОРИЯ И ОБЕЩАНИЕ},
автор={Оливье Л. де Век},
год = {2004}
}
Фрэнсис И. Эджворт (1845-1926) и Вильфредо Парето (1848-1923) впервые представили концепцию неполноценности в контексте экономика. С тех пор многокритериальная оптимизация проникла в проектирование и проектирование и развивалась все более быстрыми темпами. Strategic.mit.edu Обзор многокритериальной оптимизации: методы и ее применение
9005 многокритериальные функции объединены в единое решение с использованием весов, а решение представляет собой компонент показателей эффективности, формирующий скалярную функцию, которая включена в фитнес-функцию. Многокритериальный эволюционный алгоритм с контролируемым фокусом на коленях фронта Парето В этой статье представлена схема отбора, которая позволяет многокритериальному эволюционному алгоритму (MOEA) получить недоминируемое множество с контролируемой концентрацией вокруг существующих коленных участков фронта Парето и демонстрирует что сходимость на фронте Паредто не скомпрометирована навязыванием смещения, основанного на предпочтениях. Многокритериальное оптимальное управление ветряными турбинами: обзор методов и рекомендации по реализации
Основная цель этой работы состоит в том, чтобы изучить опыт применения старых и новых методов MOO с точки зрения практического проектирования систем управления, предлагая , некоторые открытые темы и советы по дизайну. Неопределенный междисциплинарный метод оптимизации проектирования с использованием интервальных выпуклых моделей
Неопределенная многоцелевая многодисциплинарная методология оптимизации проектирования, которая использует интервальную модель для представления неопределенностей неопределенных, но ограниченных параметров, а степень удовлетворения интервалов используется для преобразования обоих неопределенные ограничения неравенства и равенства к детерминированным ограничениям неравенства. Многоцелевые методы оптимизации как стратегия принятия решенийВ этом исследовании представлено краткое определение формулировки, представления и решения проблемы МОО и сделан вывод о том, что дерево методов МОО можно разделить на четыре основные ветви на основе артикуляции предпочтений DM: отсутствие предпочтений, априорные, интерактивные и апостериорные предпочтения. ДМ. Использование теории оптимальности и опорных точек для улучшения разнообразия и сходимости нечетко-адаптивного многоцелевого оптимизатора роя частиц
Измерение близости KKT включено в исходный Adaptive CoevolutionaryMulti-Objective Swarm Optimizer (ACMOPSO) для отслеживания сходимости подроев по направлению к Парето-оптимальному фронту и предоставления обратной связи Контроллеры нечеткой логики (FLC) типа Мамдани, которые используются для онлайн-адаптации алгоритмических параметров. Пропорционально-интегральная политика управления двумя связанными одновременными процессами оптимизации конструкции
предложено и учитывается влияние проектной переменной одной оптимизационной задачи на целевую функцию другой. Диспетчер многокритериальной оптимизации для микросетей с высоким проникновением возобновляемой генерацииБлагодаря внедрению микросетевого контроллера можно добиться многих преимуществ, таких как минимизация затрат, снижение пиковой мощности, сглаживание мощности, сокращение выбросов парниковых газов и увеличение… Оценка эффективности алгоритмов метаэвристической оптимизации: исчерпывающий обзор Чрезвычайно важно использовать правильный инструмент для измерения производительности разнообразного набора метаэвристических алгоритмов, чтобы получить соответствующее суждение о превосходстве алгоритмов, а также для подтверждения утверждений, выдвинутых исследователями для их конкретных целей. Пропорционально-интегральная политика управления двумя связанными параллельными процессами оптимизации проектированияВ этой статье исследуется управление двумя связанными процессами оптимизации проектирования, для которых предлагается пропорционально-интегральная (PI) политика управления и влияние проектной переменной одной задачи оптимизации по целевой функции другой. ПОКАЗЫВАЮТСЯ 1-10 ИЗ 19 ССЫЛОК СОРТИРОВАТЬ ПОРелевантностьНаиболее влиятельные документыНедавность Обзор многокритериальной оптимизации или задачи векторного максимума, часть I: 1776–1960
представлены. Сначала дается краткий биографический очерк Вильфредо Парето. Затем более-менее одновременное развитие… От сомнительного построения целевых функций к применению физического программирования
С помощью аналитических, графических и вычислительных средств показано, как подход физического программирования полностью обходит зависимость от веса, что приводит к новому методу практического и общая применимость. Адаптивный метод взвешенных сумм для двухкритериальной оптимизации: генерация фронта Парето
В этой статье представлен новый метод, который эффективно определяет фронт Парето для двухцелевой оптимизации с потенциальным применением к множеству целей путем адаптивного изменения весов, а не с помощью априорного выбора весов, и путем указания дополнительных ограничений неравенства. ПЕРЕСЕЧЕНИЕ НОРМАЛЬНЫХ ГРАНИЦ: АЛЬТЕРНАТИВНЫЙ МЕТОД ПОЛУЧЕНИЯ ОПТИМАЛЬНЫХ ПО ПАРЕТО ТОЧЕК В МНОГОКРИТЕРИАЛЬНЫХ ЗАДАЧАХ ОПТИМИЗАЦИИ
Можно строго доказать, что этот метод может быть легко расширен в случае более чем двух целей, сохраняя вычислительную эффективность алгоритмов типа продолжения, что является улучшением по сравнению с гомотопическим Методы отслеживания кривой компромисса. Количественная оценка внедрения технологий в группировки спутников связи
Представлена методология количественной оценки новых технологий в контексте группировок спутников связи, позволяющая найти оптимальный по Парето набор архитектур на основе зрелых, передовых технологий и анализ допустимых пар технологий для прогнозирования их совместного действия. Несовершенство метода взвешивания при многокритериальной оптимизации структур
Хорошо известно, что метод взвешивания может не дать оптимального по Парето набора многокритериальной задачи в невыпуклых случаях. В этой статье два простых примера ферм, один статический и один… Следующее поколение интерферометрических решеток радиотелескопов требует тщательного проектирования конфигурации решеток для оптимизации работы всей системы. Оптимизация множественных критериев: теория, вычисление и приложение
Математические темы из -за грипов. о служебных функциях параметрического программирования Objective Row,… Управление продукцией: стоимость, качество, себестоимость, цена, прибыль и организация
Реализация продукции на мировом рынке. Мотивация и потребительское поведение. Модель предприятия. Определение качества. Прогнозирование стоимости будущих продуктов. Тотальное управление качеством. Продукт… Поэтапное развертывание спутниковых группировок связи на низкой околоземной орбите Этот подход предоставляет проектировщикам и менеджерам систем реальные возможности, которые позволяют им сопоставить путь развития системы с фактическим сценарием развертывания спроса и демонстрирует значительные экономические преимущества предложенного подход применительно к созвездиям спутников связи на низкой околоземной орбите (НОО). |


 ..
.. А.
А.


 : Это просто случилось. Выпущена новая версия pymoo (версия 0.6.0 ). Многое произошло под капотом; однако кодовая база немного изменилась. Индивидуальный класс был перереализован, и метаалгоритмы теперь могут быть построены намного проще. Добавлены новые алгоритмы (G3PXC, RVEA, SMS-EMOA), доступны задачи динамической оптимизации и простая реализация D-NSGA-II. Для получения более подробной информации, пожалуйста, просмотрите журналы изменений. (Примечания к выпуску)
: Это просто случилось. Выпущена новая версия pymoo (версия 0.6.0 ). Многое произошло под капотом; однако кодовая база немного изменилась. Индивидуальный класс был перереализован, и метаалгоритмы теперь могут быть построены намного проще. Добавлены новые алгоритмы (G3PXC, RVEA, SMS-EMOA), доступны задачи динамической оптимизации и простая реализация D-NSGA-II. Для получения более подробной информации, пожалуйста, просмотрите журналы изменений. (Примечания к выпуску) Для получения более подробной информации, пожалуйста, просмотрите журналы изменений.
Для получения более подробной информации, пожалуйста, просмотрите журналы изменений. Каждый алгоритм разрабатывается максимально близко к предлагаемому
Каждый алгоритм разрабатывается максимально близко к предлагаемому
 Наша лаборатория, решающая практические задачи, имеет высокий приоритет для каждого студента и может помочь вам извлечь выгоду из полученного нами исследовательского опыта.
Наша лаборатория, решающая практические задачи, имеет высокий приоритет для каждого студента и может помочь вам извлечь выгоду из полученного нами исследовательского опыта. 6.0
6.0 В этой статье дается краткий обзор истории многокритериальной оптимизации и обосновывается ее важность в контексте проектирования и проектирования сложных систем. Краткий обзор методов отличает…
В этой статье дается краткий обзор истории многокритериальной оптимизации и обосновывается ее важность в контексте проектирования и проектирования сложных систем. Краткий обзор методов отличает…