Методы неравномерных покрытий и их применение для решения задач глобальной оптимизации в диалоговом режиме тема диссертации и автореферата по ВАК 05.13.02, кандидат физико-математических наук Потапов, Михаил Андреевич. Жадан методы оптимизации

Курса по выбору МЕТОДЫ ОПТИМИЗАЦИИ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

МОСКОВСКИЙ ФИЗИКО-ТЕХНИЧЕСКИЙ ИНСТИТУТ

(ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ)

УТВЕРЖДАЮ

Проректор по учебной работе

Д.А. Зубцов

22 июня 2012 г.

П Р О Г Р А М М А

курса по выбору МЕТОДЫ ОПТИМИЗАЦИИ

по направлению 010900

факультет ФУПМ

кафедра математических основ управления

курс III

семестр 5,6

Трудоёмкость: базовая часть – 0 зач. ед.

вариативная часть – 5 зач. ед.

по выбору студента – 0 зач. ед.

лекции – 66 часов Экзамен – 5,6 семестр

практические занятия – 66 часа Диф. зачет – нет

самостоятельная работа – 20 часов

ВСЕГО ЧАСОВ – 132

Программу составили:

д.ф.-м.н., проф., В.Г. Жадан,

к.ф.-м.н., доцент А.Г. Бирюков,

к.ф.-м.н. доцент Р.В. Константинов,

к.ф.-м.н. О.С. Федько,

ассистент П.Е. Двуреченский,

ассистент А.А. Орлов

Программа принята на заседании

кафедры математических основ управления

15 июня 2012 года

Заведующий кафедрой С. А. Гуз

Часть I. Элементы теории

Постановка задач оптимизации. Локальный и глобальный экстремумы. Классификация экстремальных задач. Примеры.
Выпуклые множества. Пересечение и линейная комбинация выпуклых множеств, их свойства. Конус, выпуклый конус. Аффинное множество, две формы представления аффинного множества. Выпуклая, неотрицательная и аффинная комбинация точек. Выпуклая, коническая и аффинная оболочки множеств. Их связь с комбинациями точек.
Относительная внутренность и относительная граница множества. Свойства относительной внутренности выпуклого множества.
Отделимость множеств. Свойства отделимости выпуклых множеств. Опорная гиперплоскость. Существование опорной гиперплоскости. Проекция точки на множество. Свойства проекций.
Сопряженное множество. Второе сопряженное множество. Их свойства. Сопряженный конус и сопряженное линейное подпространство. Конус, двойственный к сумме конусов, и конус, сопряженный к пересечению конусов.
Многогранные множества, полиэдры. Множество, сопряженное к многогранному множеству.
Системы линейных равенств и неравенств. Теоремы об альтернативах. Лемма Фаркаша. Линейные матричные неравенства.
Выпуклые, строго выпуклые и сильно выпуклые функции. Определения, примеры, свойства. Множество уровня выпуклой и сильно выпуклой функции. Эпиграф функции, свойства эпиграфа выпуклой функции.
Непрерывность и дифференцируемость по направлению выпуклой функции. Дифференциальные критерии выпуклой (сильно выпуклой) функции.
Субдифференциал функции. Существование и свойства субдифференциала. Теорема о субдифференциале суммы выпуклых функций.
Индикаторная функция множества. Субдифференциал индикаторной функции выпуклого множества. Субдифференциал выпуклой функции на выпуклом множестве. Опорная функция множества.
Сопряженные и полярные функции, их свойства. Неравенства Юнга–Фенхеля и Минковского–Малера. Примеры сопряженных и полярных функций.
Теорема Вейерштрасса и её следствия. Выпуклая задача минимизации. Теорема о глобальном экстремуме. Условия оптимальности выпуклых задач минимизации в терминах субдифференциалов.
Касательное направление, касательный конус. Конус возможных направлений. Их свойства. Теорема о необходимом условии экстремума в терминах производных по касательному направлению. Необходимое и достаточное условие экстремума для выпуклой задачи в терминах производных по направлению.
Необходимое и достаточное условия экстремума дифференцируемой функции на выпуклом множестве. Вариационное неравенство. Необходимые и достаточные условия экстремума для задачи безусловной минимизации (БМ).
Необходимые и достаточные условия оптимальности для задач математического программирования. Условия Каруша–Куна–Таккера. Достаточные условия второго порядка. Условия регулярности ограничений. Необходимые и достаточные условия оптимальности для выпуклой задачи математического программирования. Регулярная и нерегулярная задачи математического программирования.
Функция Лагранжа для задач математического программирования и ее свойства. Седловая точка функции Лагранжа.
Теория двойственности для задач математического программирования. Задача линейного программирования и двойственная к ней. Собственные и несобственные задачи математического программирования. Двойственность для несобственных задач линейного программирования.

Часть 2. Численные методы

Понятие о численных методах оптимизации. Сходимость и условия остановки численных методов.
Унимодальные функции одной переменной. Методы одномерной минимизации (метод дихотомии, метод золотого сечения, метод Фибоначчи).
Численные методы решения задачи БМ. Способы выбора шага в методах. Наискорейший спуск. Правило Армихо, правило Голдстейна. Градиентный метод и метод Ньютона решения задачи БМ. Свойства их сходимости. Квазиньютоновские методы.
Сопряженные направления. Метод сопряженных градиентов для минимизации квадратичных функций. Метод сопряженных градиентов для решения общей задачи БМ.
Задача линейного программирования (ЛП). Общая, каноническая и другие формы задачи ЛП. Угловые точки в задаче ЛП. Алгебраический критерий угловой точки.
Симплекс-метод решения задачи ЛП. Табличная форма СМ. Модифицированный СМ решения задачи ЛП. Двухфазный симплекс-метод. М-задача.
Методы решения задач с простыми ограничениями. Метод проекции градиента. Метод условного градиента.

Метод возможных направлений и метод линеаризации. Различные варианты вспомогательных задач для выбора возможных направлений.
Общая схема метода штрафных функций. Метод внешних штрафных функций. Метод внутренних штрафных функций (барьерных функций). Свойства сходимости методов штрафных функций.
Методы параметризации целевых функций (метод внешних центров). Метод внешних центров для задач выпуклого программирования.
Модифицированные функции Лагранжа для задач с ограничениями типа равенства. Их обобщение на задачи с неравенствами. Методы последовательного квадратичного программирования.
Мультипликативно-барьерные методы для задач ЛП. Аффинно-масштабирующий метод и метод Кармаркара для задачи ЛП. Прямо-двойственный метод центрального пути для ЛП и КП.
Задачи многокритериальной оптимизации. Понятие оптимальности в многокритериальной оптимизации. Оптимальные по Слейтеру и Парето решения задач многокритериальной оптимизации. Модификация метода внешних центров для задач многокритериальной оптимизации.

Методы глобальной оптимизации. Построение нижних аппроксимаций для липшицевых функций. Метод секущих и метод покрытий.

Литература

Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации. – М.: Наука, 1986 (+2008).
Васильев Ф.П. Численные методы решения экстремальных задач. – М.: Наука, 1988 (+2011).
Поляк Б.Т. Введение в оптимизацию. – М.: Наука, 1983.
Бирюков С.И. Оптимизация. – М.: МФТИ, 2003.
Бирюков А.Г. Методы оптимизации. Условия оптимальности в экстремальных задачах. – М.: МФТИ, 2010.
Моисеев Н.Н., Иванилов Ю.П., Столярова Е.М. Методы оптимизации. – М.: Наука, 1978.
Евтушенко Ю.Г. Методы решения экстремальных задач и их применение в системах оптимизации. – М.: Наука, 1982.
Измайлов А.Ф., Солодов М.В. Численные методы оптимизации. – М.: Физматлит, 2003.
Жадан В.Г. Численные методы линейного и нелинейного программирования. Вспомогательные функции в условной оптимизации. – М.: ВЦ РАН, 2002.
Галеев Э.М. Тихомиров В.М. Оптимизация. Теория. Примеры. Задачи. – Эдиториал УРСС, 2000.
Ю.Е. Нестеров. Введение в выпуклую оптимизацию. МЦНМО, 2010.
Ляшенко И.Н., Карагодова Е.Н., Черникова Н.В., Шор Н.З. Линейное и нелинейное программирование. – Киев, 1975.

ЗАДАНИЕ № 1

Используя геометрические интерпретации, решить следующие экстремальные задачи:

Указать, какие из решений этих задач являются локальными, глобальными, строгими, острыми.

Решить задачу:

Найти экстремумы в следующей задаче:

Решить задачу:

Пусть

Найти опорные гиперплоскости ко множеству G в точках экстремума для задачи:

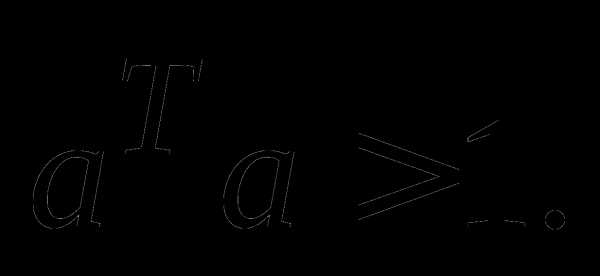
1) Пусть 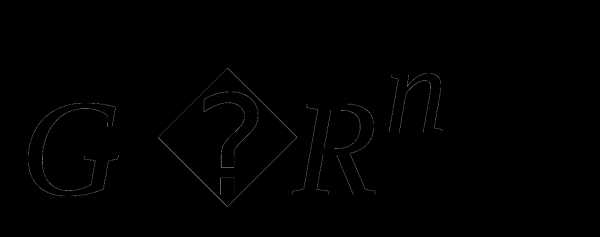замкнутое множество, 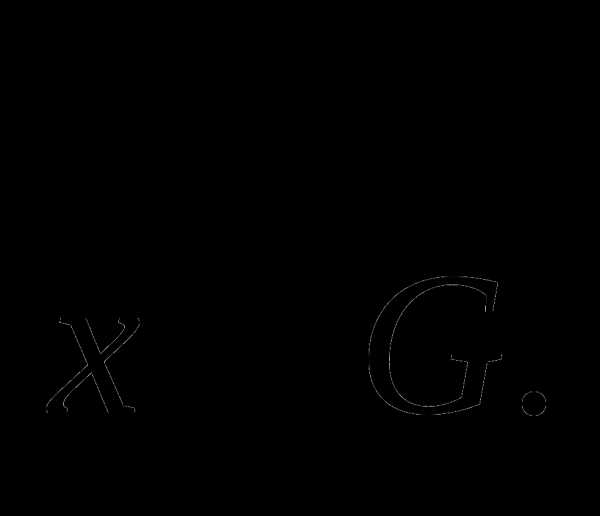Найти множество Рассмотреть случаи выпуклого и невыпуклого множеств

2) Пусть даны 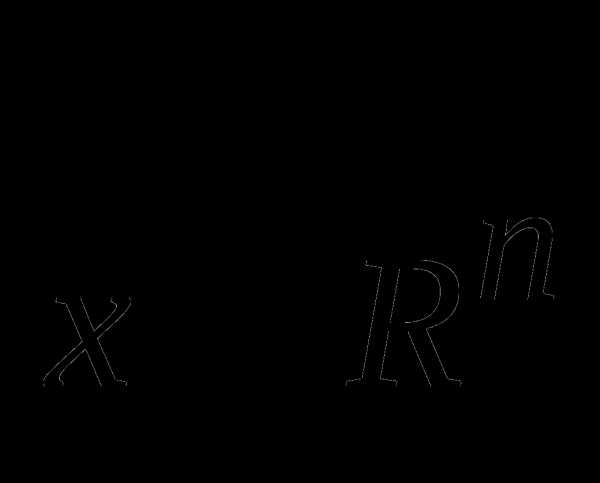и выпуклый конус .

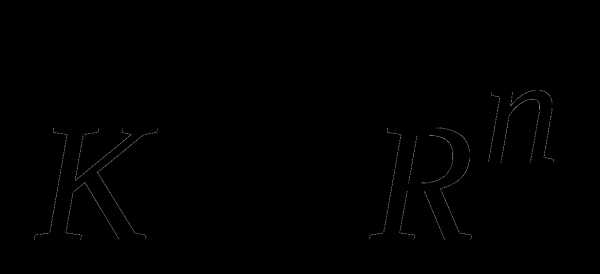Пусть 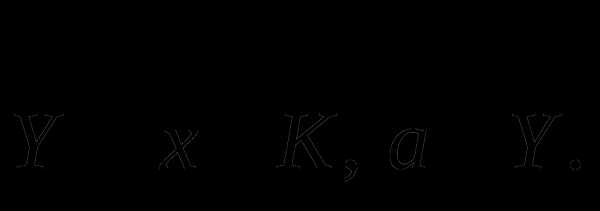Найти множества

3) Пусть 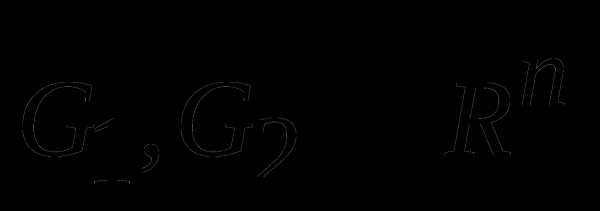- замкнутые множества и 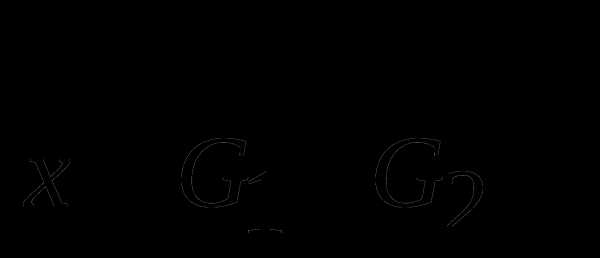единственная точка. Каким условиям удовлетворяют множества 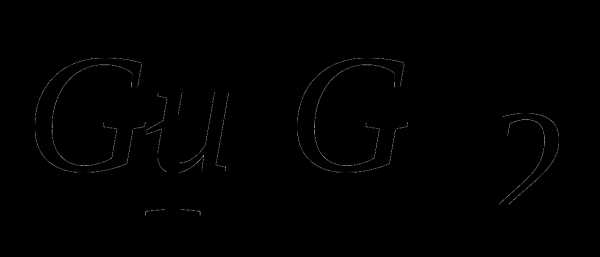, если:

а)

б)

1) Показать, что конусом, сопряженным к конусу

является конус

2) Найти

Определить расстояние между множествам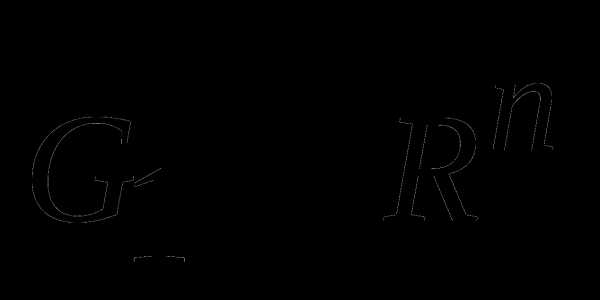и и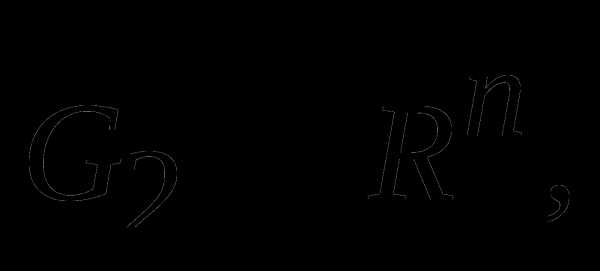

а также уравнения двух разделяющих гиперплоскостей, одна из которых является опорной ко множеству 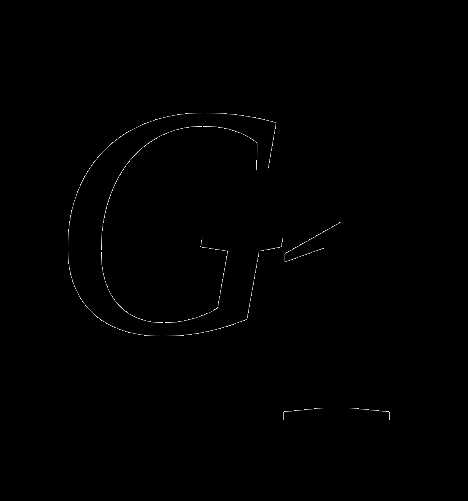, другая – ко множеству в точках, для которых расстояние минимально

Соответствующую задачу оптимизации решить методом множителей Лагранжа.

а) Пусть даны матрицы

Рассмотреть частные случаи:

Здесь 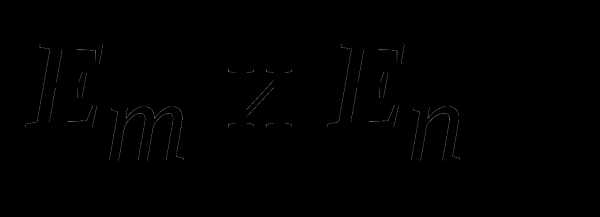единичные матрицы порядка m и nсоответственно. Для всех случаев найти где число

б) Пусть даны матрицы

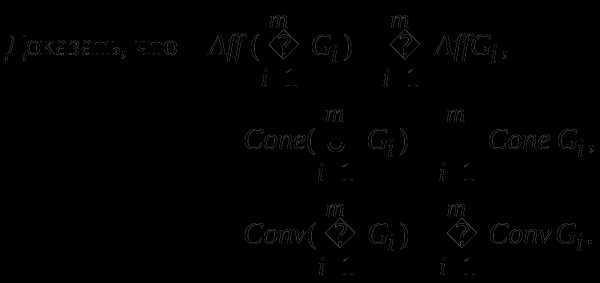
Доказать, что

Рассмотреть частный случай, когда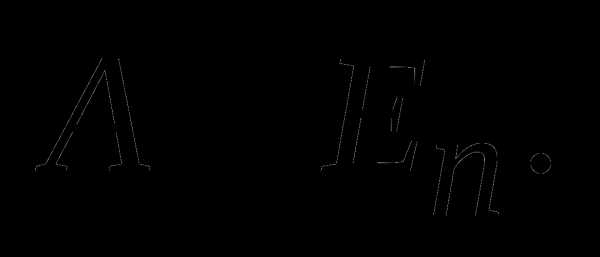

ЗАДАНИЕ № 2

а) Пусть 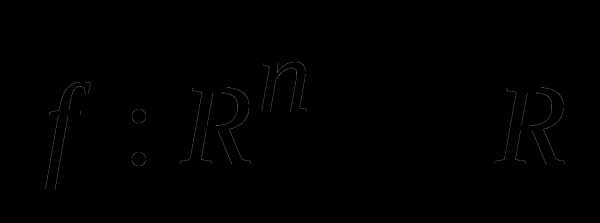выпуклая функция. Доказать, что для всех Для функций 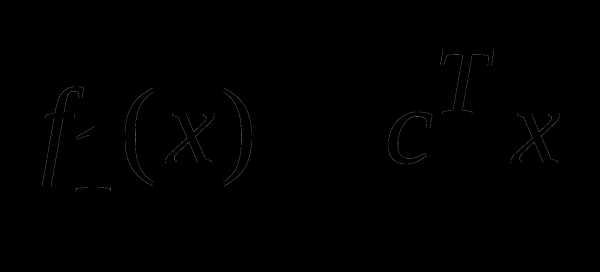и
найти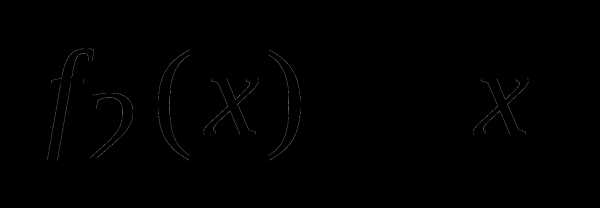

б) Найти опорную функцию для множеств:

Найти 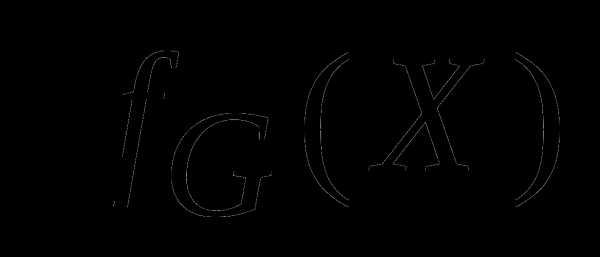функции

на множестве

Показать, что экстремальная задача регулярна: min f(x),

Решить экстремальную задачу

если

Показать, что в точках решения выполнено необходимое и достаточное условие экстремума.

Решить задачу

для чего найти точки ,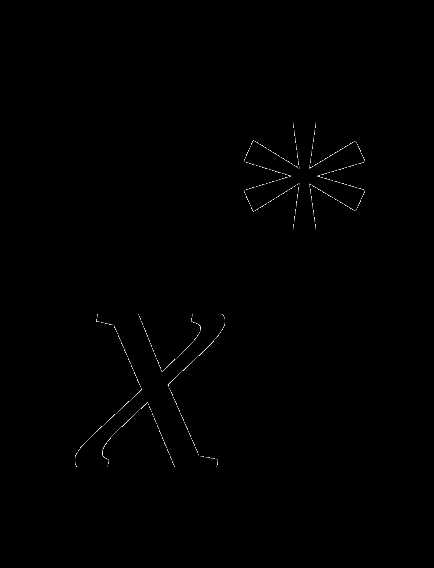

где ,и выяснить, какие из них являются точками локального и глобального, строгого и острого экстремума.

Решить задачу БМ:

Решить задачу

Решить методом множителей Лагранжа задачу:

Построить задачу, двойственную к следующей:

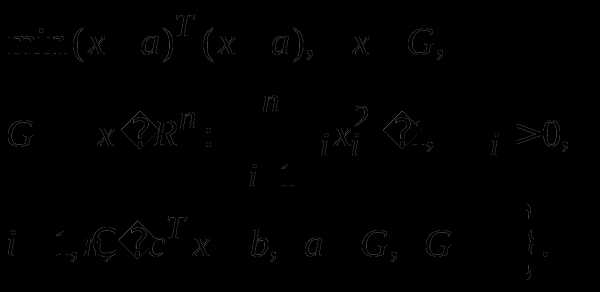
Найти функции, сопряженные к функциям:

Для задачи min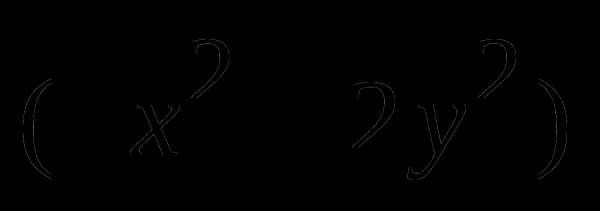, где

найти седловую точку, решая задачу «в лоб», а именно:

а) считая множители Лагранжа параметрами, найти из решения задачи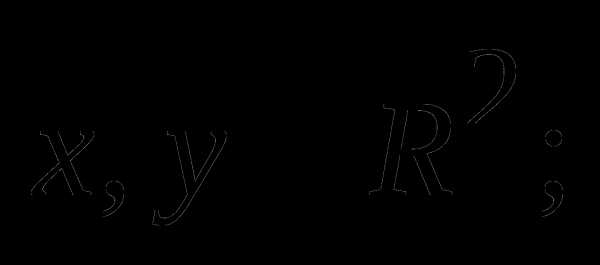

б) найти 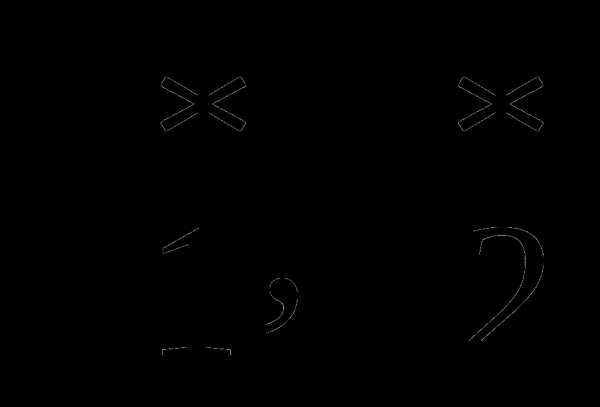из решения задачи

в) сравнить решения с решением, полученным из условия оптимальности ККТ.

В выпуклой задаче

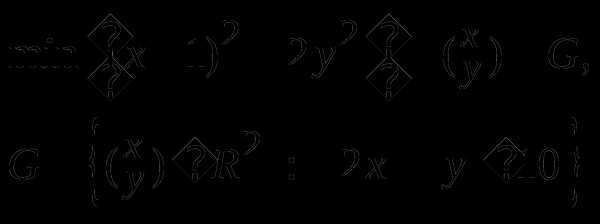
а) найти множество стационарных точек:

б) решить двойственную задачу:

в) найти седловую точку 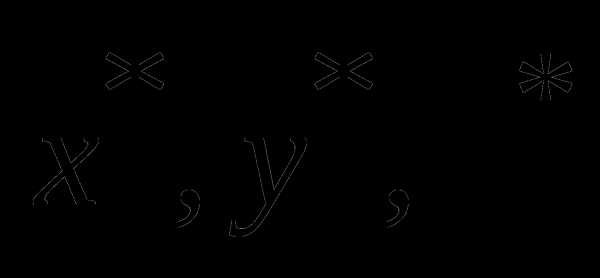функции Лагранжа.

ЗАДАНИЕ № 3

1. Найти стационарные точки и точки экстремума функции

Сделать по одному шагу методом наискорейшего спуска (НС) из начальных точек

Оценить значение коэффициента скорости сходимости в методе НС для итерационных процессов, для которых

точки локальных минимумов, к которым сходится метод НС из указанных точек 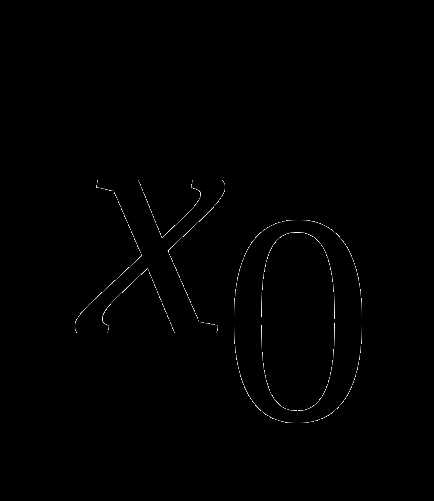. Найти предельное значение коэффициента скорости сходимости.

2. Для решения задачи при условии с e-точностью методами дихотомии, золотого сечения и Фибоначчи найти число вычислений функции для e = 10–7и e = 10–10.

3. Какую скорость сходимости к точке минимума имеет метод Ньютона при минимизации функций если

где –симметричная положительно определенная матрица,

Пусть векторы – линейно независимы, Построим систему векторов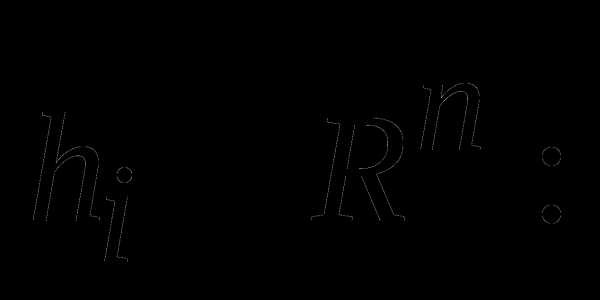

при этом система такова, что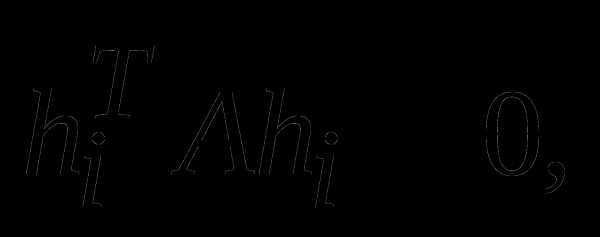

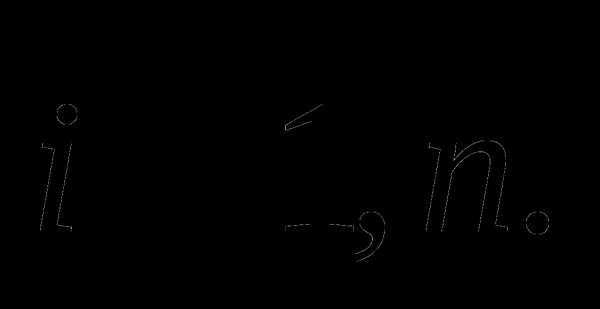
Доказать, что векторы , сопряжены относительно матрицы А, а также справедливо соотношение

(*)

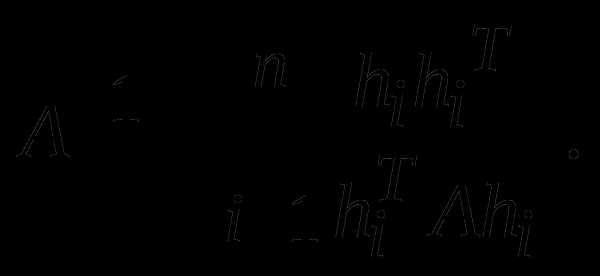Используя формулу (*), решить систему линейных уравнений (**), когда система

предварительно симметризовав её.

5. Показать, что в методе сопряженных градиентов для квадратичной функции f(х) на каждом k-м шаге при (вектор направления убывания: ) в точке реализуется минимум функции f(х) на аффинном множестве

6. Определить скорость сходимости метода Ньютона и метода наискорейшего спуска и окрестность, из которой эти методы сходятся к оптимальному решению следующей задачи:

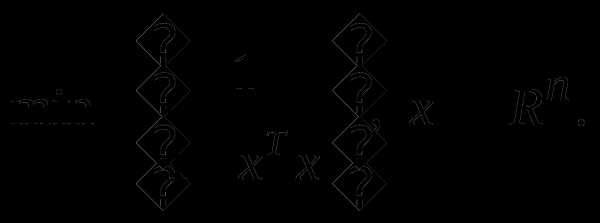
Замечание: При решении задачи замену переменных 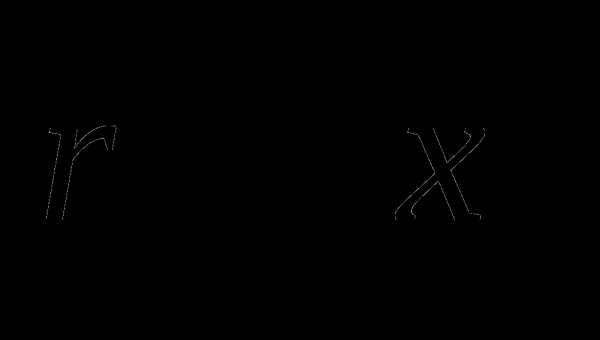не использовать.

7. Найти минимум функции методом Ньютона и методом сопряженных градиентов, где

8. Найти при условиях: методом множителей Лагранжа. Построить для данной задачи двойственную и решить ее. Сравнить решения этих задач.

9. Для задачи непрерывно дифференцируемая функция, сформулировать необходимые условия экстремума, если

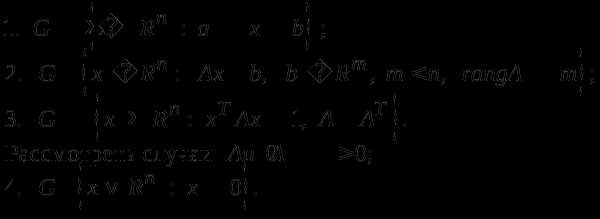
Сформулировать для указанных задач достаточные условия экстремума первого порядка, второго порядка, достаточные условия острого экстремума. Сформулировать для задачи математического программирования необходимые и достаточные условия оптимальности первого и второго порядков.

10. Рассмотрим задачу № 1 (КЗ) и задачу № 2 (МП):

где функции – непрерывно дифференцируемые. Представим задачу МП в следующем виде:

Используя для задачи № 3 теорему о необходимом условии оптимальности для задачи № 1 (метод множителей Лагранжа для К 3; теор. 1.5, глава 1), доказать следующую теорему для задачи МП (см ).

Теорема (ККТ). Пусть в задаче МП функции f и непрерывно дифференцируемы в окрестности некоторой допустимой точки линейно независимы. Тогда если решение задачи МП, то существует единственный вектор 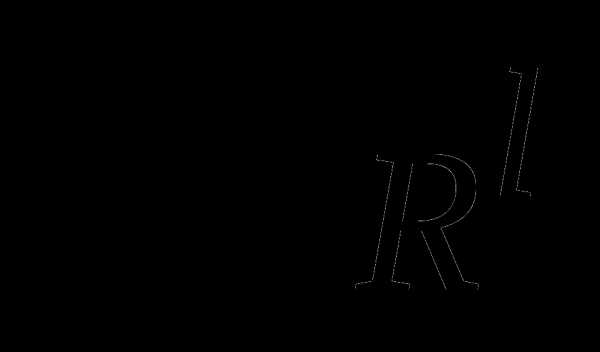такой, что

– множество индексов активных ограничений.

ЗАДАНИЕ № 4

1. Для задачи ЛП

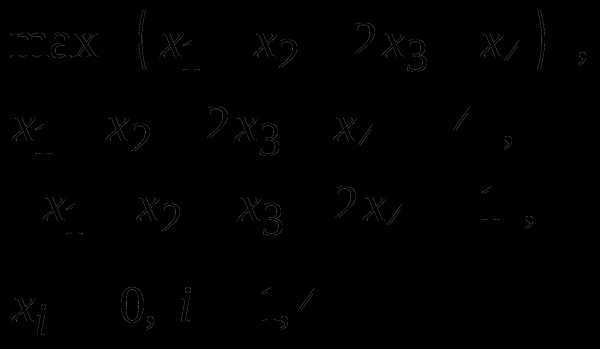
построить двойственную задачу, решить её, после чего решить прямую задачу.

2. Найти решение задачи

зависящее от параметров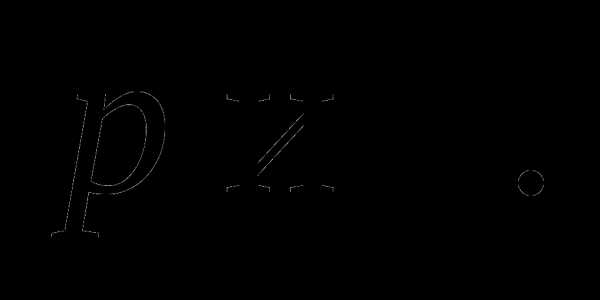

3. Следующую задачу линейного программирования решить табличным симплекс-методом :

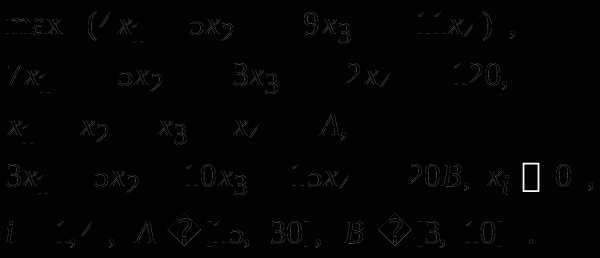
Найти решение соответствующей двойственной задачи.

Указание. Конкретные значения параметров A и B получить у своего преподавателя.

Пусть матрица Методом внешних штрафных функций решить задачу 1: 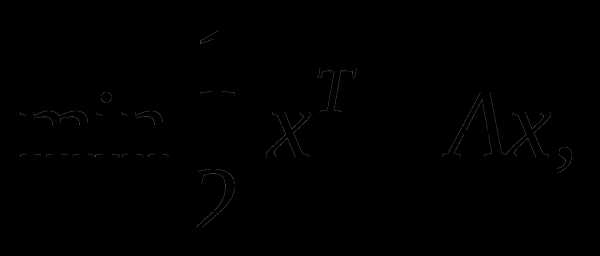при условии 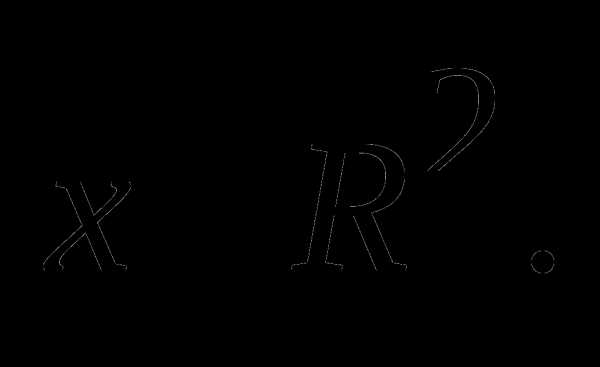Методом внутренних штрафных функций решить задачу 2: 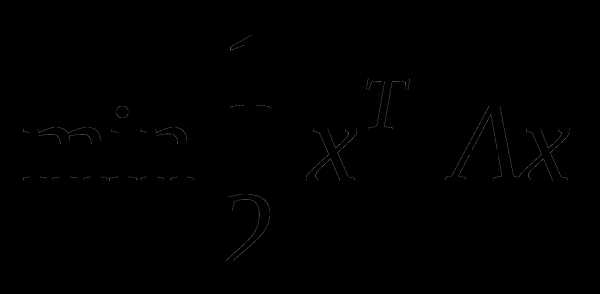при условии .

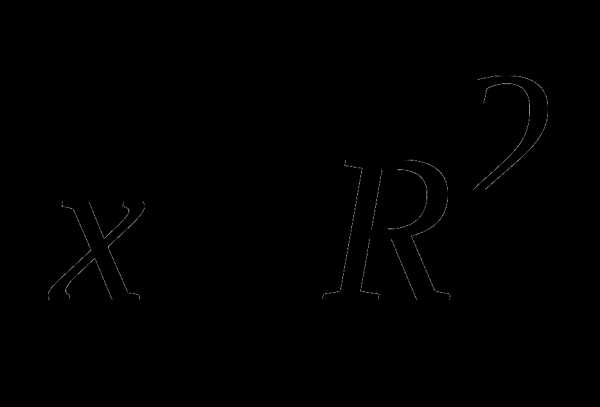5. Решить методом точных внешних штрафных функций задачу: найти

6. Методом условного градиента решить задачу: найти

при условиях Начальная точка x0 = (0, 1). Длина шага a вдоль направления h определяется из условия одномерной максимизации.

Методом проекции градиента (схема № 2) решить задачу при условиях:

Начальная точка

Методом возможных направлений решить следующую задачу: 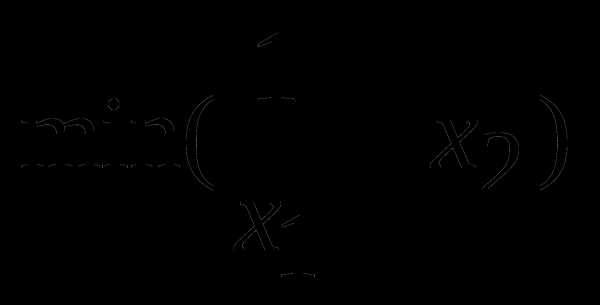при условиях: Начальная точка

9. Методом модифицированных функций Лагранжа решить задачи.

Найти предельное значение множителя Лагранжа 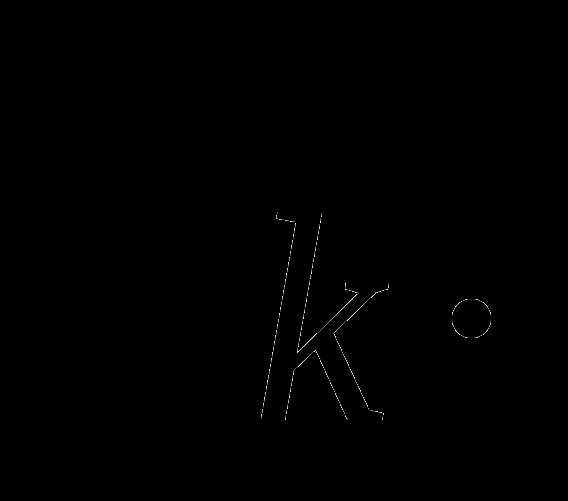Оценить коэффициенты скорости сходимости последовательностей

Указание. При необходимости воспользоваться формулами из задачи № 11, задание № 1.

10. Методом параметризации целевой функции решить задачу при условии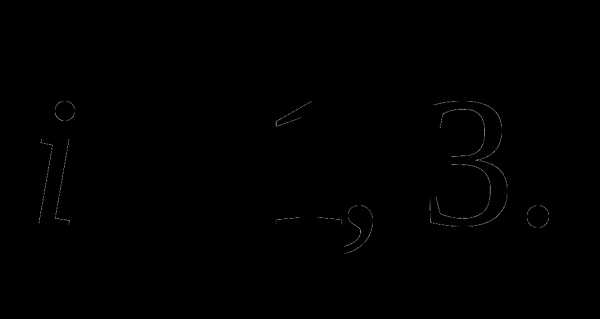

11. Найти барьерно-проективным методом расстояние от начала координат до выпуклой оболочки точек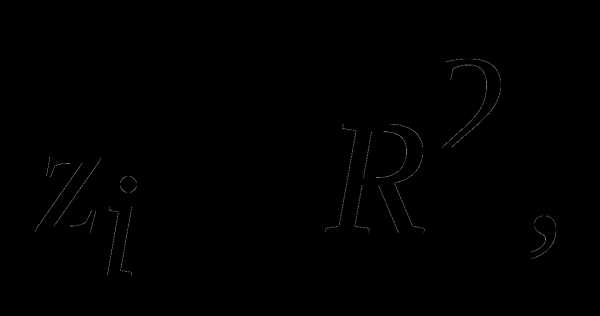

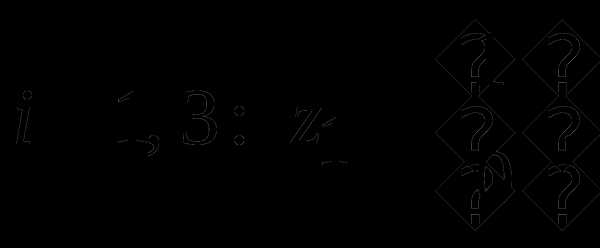
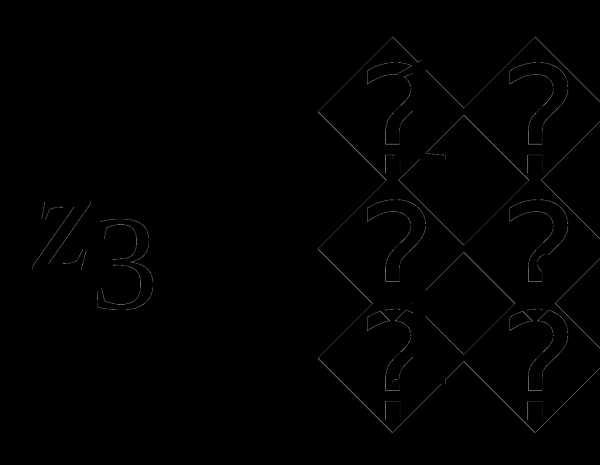
Указание. Свести задачу к задаче условной минимизации на симплексе.

Подписано в печать 29.06.2012. Формат 60 ´ 84.

Усл. печ. л. 0,25. Тираж 125 экз. Заказ № 184

Федеральное государственное автономное образовательное учреждение

высшего профессионального образования

«Московский физико-технический институт

(государственный университет)»

Отдел оперативной полиграфии «Физтех-полиграф»

141700, Московская обл., г. Долгопрудный, Институтский пер., 9

E-mail: rio@

textarchive.ru

010900 «Прикладные математика и физика»

Программа по дисциплине: Методы оптимизации по направлению: 010900 «Прикладные математика - страница №1/1

министерство образования и науки российской федерации

московский физико-технический институт

(государственный унивеситет)

УТВЕРЖДАЮ

Проректор по учебной работе

_____________Д.А. Зубцов

28 июня 2013 г.

ПРОГРАММА

по дисциплине: Методы оптимизации

по направлению: 010900 «Прикладные математика и физика»

факультет: ФУПМ

кафедра: математических основ управления

курс: III

семестры: 5, 6

Трудоёмкость: базовая часть – 5 зач. ед.

вариативная часть – 5 зач. ед.

по выбору студента – 0 зач. ед.

лекции – 66 часов Экзамен – 5, 6 семестр

практические (семинарские)

занятия – 66 часа Диф. зачет – нет

лабораторные занятия – нет

Самостоятельная работа – 20 часов

ВСЕГО ЧАСОВ – 132

Программу составили:

д.ф.-м.н., профессор В.Г. Жадан, к.ф.-м.н., доцент А.Г. Бирюков,

к.ф.-м.н. доцент Р.В. Константинов, к.ф.-м.н. О.С. Федько,

к.ф.-м.н. А.А. Орлов, ассистент П.Е. Двуреченский,

ассистент Ю.В. Дорн

Программа принята на заседании

кафедры математических основ управления

26 апреля 2013 года Заведующий кафедрой С. А. Гуз

Часть I. Элементы теории

Постановка задач оптимизации. Локальный и глобальный экстремумы. Классификация экстремальных задач. Примеры.
Выпуклые множества. Пересечение и линейная комбинация выпуклых множеств, их свойства. Конус, выпуклый конус. Аффинное множество, две формы представления аффинного множества. Выпуклая, неотрицательная и аффинная комбинация точек. Выпуклая, коническая и аффинная оболочки множеств. Их связь с комбинациями точек.
Относительная внутренность и относительная граница множества. Свойства относительной внутренности выпуклого множества.
Отделимость множеств. Свойства отделимости выпуклых множеств. Опорная гиперплоскость. Существование опорной гиперплоскости. Проекция точки на множество. Свойства проекций.
Сопряженное множество. Второе сопряженное множество. Их свойства. Сопряженный конус и сопряженное линейное подпространство. Конус, двойственный к сумме конусов, и конус, сопряженный к пересечению конусов.
Многогранные множества, полиэдры. Множество, сопряженное к многогранному множеству.
Системы линейных равенств и неравенств. Теоремы об альтернативах. Лемма Фаркаша. Линейные матричные неравенства.
Выпуклые, строго выпуклые и сильно выпуклые функции. Определения, примеры, свойства. Множество уровня выпуклой и сильно выпуклой функции. Эпиграф функции, свойства эпиграфа выпуклой функции.
Непрерывность и дифференцируемость по направлению выпуклой функции. Дифференциальные критерии выпуклой (сильно выпуклой) функции.
Субдифференциал функции. Существование и свойства субдифференциала. Теорема о субдифференциале суммы выпуклых функций.
Индикаторная функция множества. Субдифференциал индикаторной функции выпуклого множества. Субдифференциал выпуклой функции на выпуклом множестве. Опорная функция множества.
Сопряженные и полярные функции, их свойства. Неравенства Юнга–Фенхеля и Минковского–Малера. Примеры сопряженных и полярных функций.
Теорема Вейерштрасса и её следствия. Выпуклая задача минимизации. Теорема о глобальном экстремуме. Условия оптимальности выпуклых задач минимизации в терминах субдифференциалов.
Касательное направление, касательный конус. Конус возможных направлений. Их свойства. Теорема о необходимом условии экстремума в терминах производных по касательному направлению. Необходимое и достаточное условие экстремума для выпуклой задачи в терминах производных по направлению.
Необходимое и достаточное условия экстремума дифференцируемой функции на выпуклом множестве. Вариационное неравенство. Необходимые и достаточные условия экстремума для задачи безусловной минимизации (БМ).
Необходимые и достаточные условия оптимальности для задач математического программирования. Условия Каруша–Куна–Таккера. Достаточные условия второго порядка. Условия регулярности ограничений. Необходимые и достаточные условия оптимальности для выпуклой задачи математического программирования. Регулярная и нерегулярная задачи математического программирования.
Функция Лагранжа для задач математического программирования и ее свойства. Седловая точка функции Лагранжа.
Теория двойственности для задач математического программирования. Задача линейного программирования и двойственная к ней. Собственные и несобственные задачи математического программирования. Двойственность для несобственных задач линейного программирования.

Часть 2. Численные методы

Понятие о численных методах оптимизации. Сходимость и условия остановки численных методов.
Унимодальные функции одной переменной. Методы одномерной минимизации (метод дихотомии, метод золотого сечения, метод Фибоначчи).
Численные методы решения задачи БМ. Способы выбора шага в методах. Наискорейший спуск. Правило Армихо, правило Голдстейна. Градиентный метод и метод Ньютона решения задачи БМ. Свойства их сходимости. Квазиньютоновские методы.
Сопряженные направления. Метод сопряженных градиентов для минимизации квадратичных функций. Метод сопряженных градиентов для решения общей задачи БМ.
Задача линейного программирования (ЛП). Общая, каноническая и другие формы задачи ЛП. Угловые точки в задаче ЛП. Алгебраический критерий угловой точки.
Симплекс-метод решения задачи ЛП. Табличная форма СМ. Модифицированный СМ решения задачи ЛП. Двухфазный симплекс-метод. М-задача.
Методы решения задач с простыми ограничениями. Метод проекции градиента. Метод условного градиента.
Метод возможных направлений и метод линеаризации. Различные варианты вспомогательных задач для выбора возможных направлений.
Общая схема метода штрафных функций. Метод внешних штрафных функций. Метод внутренних штрафных функций (барьерных функций). Свойства сходимости методов штрафных функций.
Методы параметризации целевых функций (метод внешних центров). Метод внешних центров для задач выпуклого программирования.
Модифицированные функции Лагранжа для задач с ограничениями типа равенства. Их обобщение на задачи с неравенствами. Методы последовательного квадратичного программирования.
Мультипликативно-барьерные методы для задач ЛП. Аффинно-масштабирующий метод и метод Кармаркара для задачи ЛП. Прямо-двойственный метод центрального пути для ЛП и КП.
Задачи многокритериальной оптимизации. Понятие оптимальности в многокритериальной оптимизации. Оптимальные по Слейтеру и Парето решения задач многокритериальной оптимизации. Модификация метода внешних центров для задач многокритериальной оптимизации.
Методы глобальной оптимизации. Построение нижних аппроксимаций для липшицевых функций. Метод секущих и метод покрытий.

Литература

Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации. – М.: Наука, 2008.
Васильев Ф.П. Численные методы решения экстремальных задач. – М.: Наука, 2011.
Бирюков С.И. Оптимизация. – М.: МФТИ, 2003.
Бирюков А.Г. Методы оптимизации. Условия оптимальности в экстремальных задачах. – М.: МФТИ, 2010.
Измайлов А.Ф., Солодов М.В. Численные методы оптимизации. – М.: Физматлит, 2003.
Жадан В.Г. Численные методы линейного и нелинейного программирования. Вспомогательные функции в условной оптимизации. – М.: ВЦ РАН, 2002.
Галеев Э.М., Тихомиров В.М. Оптимизация. Теория. Примеры. Задачи. – М.: Эдиториал УРСС, 2000.
Нестеров Ю.Е. Введение в выпуклую оптимизацию. – М.: МЦНМО, 2010.

Дополнительная литература

Поляк Б.Т. Введение в оптимизацию. – М.: Наука, 1983.
Моисеев Н.Н., Иванилов Ю.П., Столярова Е.М. Методы оптимизации. – М.: Наука, 1978.
Евтушенко Ю.Г. Методы решения экстремальных задач и их применение в системах оптимизации. – М.: Наука, 1982.

ЗАДАНИЕ № 1

Используя геометрические интерпретации, решить следующие экстремальные задачи:

Указать, какие из решений этих задач являются локальными, глобальными, строгими, острыми.

Решить задачу:

Найти экстремумы неявно заданной функции двух переменных: , если

Между точками и , расположенными на одинаковой высоте от земли, подвешена гибкая тяжелая нить с постоянной линейной плотностью кг/м. Расстояние между точками и равно . Найти такую длину нити , чтобы натяжение нити в точках подвеса и было минимальным. Уравнение точек линии в декартовой прямоугольной системе координат , начало которой находится в точке , ось проходит через точки и , ось параллельна ускорению свободного падения, имеет вид , где – параметр, зависящий от длины нити .
Решить задачу:

Пусть

Найти опорные гиперплоскости ко множеству в точках экстремума для задачи:

8. 1) Пусть замкнутое множество, Найти множество Рассмотреть случаи выпуклого и невыпуклого множеств

2) Пусть даны и выпуклый конус .

Пусть Найти множества

3) Пусть – замкнутые множества и единственная точка. Каким условиям удовлетворяют множества , если:

а)

б)

9. 1) Показать, что конусом, сопряженным к конусу

является конус

2) Найти

10. Определить расстояние между множествами а также уравнения двух разделяющих гиперплоскостей, одна из которых является опорной ко множеству, другая – ко множеству в точках, для которых расстояние минимально:

Вычисления провести с относительной точностью

11. а) Пусть даны матрицы

Рассмотреть частные случаи:

Здесь единичные матрицы порядка m и n соответственно. Для всех случаев найти где число

б) Пусть даны матрицы

Доказать, что

Рассмотреть частный случай, когда

ЗАДАНИЕ № 2

Найти опорную функцию для множеств:

Найти функции на множестве

Показать, что экстремальная задача регулярна: ,

Решить экстремальную задачу:

если

Показать, что в точках решения выполнено необходимое и достаточное условие экстремума.

Решить задачу

для чего найти точки , где , и выяснить, какие из них являются точками локального и глобального, строгого и острого экстремума.

Решить задачу БМ:

Решить задачу

Решить методом множителей Лагранжа задачу:

Построить задачу, двойственную к следующей:

Найти функции, сопряженные к функциям:

Для задачи min, где

найти седловую точку, решая задачу «в лоб», а именно:

а) считая множители Лагранжа параметрами, найти из решения задачи

б) найти из решения задачи

в) сравнить решения с решением, полученным из условия оптимальности ККТ.

В выпуклой задаче

а) найти множество стационарных точек:

б) решить двойственную задачу:

в) найти седловую точку функции Лагранжа.

ЗАДАНИЕ № 3

1. Найти стационарные точки и точки экстремума функции

Сделать по одному шагу методом наискорейшего спуска (НС) из начальных точек

Оценить значение коэффициента скорости сходимости в методе НС для итерационных процессов, для которых

– точки локальных минимумов, к которым сходится метод НС из указанных точек . Найти предельное значение коэффициента скорости сходимости.

3. Какую скорость сходимости к точке минимума имеет метод Ньютона при минимизации функций если

где

Пусть векторы – линейно независимы, Построим систему векторов

при этом система такова, что

Доказать, что векторы , сопряжены относительно матрицы , а также справедливо соотношение

(*)

Используя формулу (*), решить систему линейных уравнений (**) предварительно ее симметризовав, для

Замечание. При решении задачи замену переменных не использовать.

7. Найти минимум функции методом Ньютона и методом сопряженных градиентов, где

9. Для задачи непрерывно дифференцируемая функция. Сформулировать необходимые условия экстремума, если

10. Пусть функции и непрерывно дифференцируемы на . Рассмотрим экстремальные задачи:

А) Найти:

Б) Найти:

где

shikardos.ru

Жадан, Виталий Григорьевич - Разработка и систематизация численных методов условной оптимизации : автореферат дис. ... доктора физико-математических наук : 05.13.16

Поиск по определенным полям

Чтобы сузить результаты поисковой выдачи, можно уточнить запрос, указав поля, по которым производить поиск. Список полей представлен выше. Например:

author:иванов

Можно искать по нескольким полям одновременно:

author:иванов title:исследование

Логически операторы

По умолчанию используется оператор AND. Оператор AND означает, что документ должен соответствовать всем элементам в группе:

исследование разработка

author:иванов title:разработка

оператор OR означает, что документ должен соответствовать одному из значений в группе:

исследование OR разработка

author:иванов OR title:разработка

оператор NOT исключает документы, содержащие данный элемент:

исследование NOT разработка

author:иванов NOT title:разработка

Тип поиска

При написании запроса можно указывать способ, по которому фраза будет искаться. Поддерживается четыре метода: поиск с учетом морфологии, без морфологии, поиск префикса, поиск фразы. По-умолчанию, поиск производится с учетом морфологии. Для поиска без морфологии, перед словами в фразе достаточно поставить знак "доллар":

$исследование $развития

Для поиска префикса нужно поставить звездочку после запроса:

исследование*

Для поиска фразы нужно заключить запрос в двойные кавычки:

"исследование и разработка"

Поиск по синонимам

Для включения в результаты поиска синонимов слова нужно поставить решётку "#" перед словом или перед выражением в скобках. В применении к одному слову для него будет найдено до трёх синонимов. В применении к выражению в скобках к каждому слову будет добавлен синоним, если он был найден. Не сочетается с поиском без морфологии, поиском по префиксу или поиском по фразе.

#исследование

Группировка

Для того, чтобы сгруппировать поисковые фразы нужно использовать скобки. Это позволяет управлять булевой логикой запроса. Например, нужно составить запрос: найти документы у которых автор Иванов или Петров, и заглавие содержит слова исследование или разработка:

author:(иванов OR петров) title:(исследование OR разработка)

Приблизительный поиск слова

Для приблизительного поиска нужно поставить тильду "~" в конце слова из фразы. Например:

бром~

При поиске будут найдены такие слова, как "бром", "ром", "пром" и т.д. Можно дополнительно указать максимальное количество возможных правок: 0, 1 или 2. Например:

бром~1

По умолчанию допускается 2 правки.

Критерий близости

Для поиска по критерию близости, нужно поставить тильду "~" в конце фразы. Например, для того, чтобы найти документы со словами исследование и разработка в пределах 2 слов, используйте следующий запрос:

"исследование разработка"~2

Релевантность выражений

Для изменения релевантности отдельных выражений в поиске используйте знак "^" в конце выражения, после чего укажите уровень релевантности этого выражения по отношению к остальным. Чем выше уровень, тем более релевантно данное выражение. Например, в данном выражении слово "исследование" в четыре раза релевантнее слова "разработка":

исследование^4 разработка

По умолчанию, уровень равен 1. Допустимые значения - положительное вещественное число.

Поиск в интервале

Для указания интервала, в котором должно находиться значение какого-то поля, следует указать в скобках граничные значения, разделенные оператором TO. Будет произведена лексикографическая сортировка.

author:[Иванов TO Петров]

Будут возвращены результаты с автором, начиная от Иванова и заканчивая Петровым, Иванов и Петров будут включены в результат.

author:{Иванов TO Петров}

Такой запрос вернёт результаты с автором, начиная от Иванова и заканчивая Петровым, но Иванов и Петров не будут включены в результат. Для того, чтобы включить значение в интервал, используйте квадратные скобки. Для исключения значения используйте фигурные скобки.

search.rsl.ru

Диссертация на тему «Исследование и разработка алгоритмов и комплекса программ для реализации модифицированного метода поиска глобального экстремума функции многих переменных» автореферат по специальности ВАК 05.13.18 - Математическое моделирование, численные методы и комплексы программ

1. Ю.Г.Евтушенко. Численный метод поиска глобального экстремума функции (перебор на неравномерной сетке) // Журнал вычисл. матем. и матем. физики, 1971. Т. 11. № 6. С. 1390-1403.

2. Пиявский С.А. Один алгоритм отыскания абсолютного экстемума функции // Журнал вычисл. матем. и матем. физики, 1972. Т. 12. № 4. С. 888-896.

3. Черноусько Ф. JI. Об оптимальном поиске экстремума унимодальных функций // Журнал вычислительной математики и математической физики. 1970, т. 10.

4. Черноусько Ф. Л. Об оптимальном поиске минимума выпуклых функций // Журнал вычислительной математики и математической физики. 1970, т. 10.

5. Кузнецов А. Г., Черноусько Ф. Л. Об оптимальном управлении, минимизирующем экстремум функции фазовых координат //Кибернетика. 1968. № 3. С. 50 -55.

6. Стронгин Р.Г. Численные методы в многоэкстремальных задачах. М.: Наука, 1978.

7. Нефедов В.Н. Отыскание глобального максимума функции нескольких переменных на множестве, заданном ограничениями типа неравенств // Журнал вычисл. математики и матем. физики, 1987. Т. 27. № 1.С. 35-51.

8. Жиглявский А.А., Жилинскас А.Г. Методы поиска глобального экстремума. М.: Наука, 1991.

9. Гергель В.П. Алгоритм глобального поиска, использующий производные // Динамика систем и оптимизация. Нижний Новгород: ННГУ, 1992. С. 161-178.

10. Я.Д.Сергеев, Д.Е.Квасов. Диагональные методы глобальной оптимизации. //ФИЗМАТЛИТ 2008. стр.9-14.

11. A.M.Rubinov and B.M.Glover. Increasing convex along rays functions with applications to global optimization. — Research Report 21/96, University of Ballarat, 1996.

12. Rinnoy Kan, A.H.G., Timmer, G.T. Stocactic global optimization methods //Mathematical programming. 39, 27-28, 1987.

13. Torn A. Global Optimization as a Combination of Global and Local Search // Turku, Abo Akademi University, HHAA A: 13, 1974.

14. Torn A., Viitanen S. Topographical Global Optimization // Floudas C.A., Pardalos P.M. (eds): Recent Advances in Global Optimization. Princeton University Press, 384-398, 1992.

15. T6rn A., Viitanen S. Topographical Global Optimization Using Pre-Sampled Points // Journal of Global Optimization, Vol 5, No 3, 267-276, 1994.

16. Evtushenko Yu. G., Potapov M. A., Korotkich V. V. Recent Advances in Global Optimization // Prinston, Princeton University Press, 274-297, 1992.

17. Moore R. Interval Analysis // New Jersey, Prentice-Hall, 1966.

18. Nemhauster G.L., Pruul E.A., Rushmeier R.A. Branch-and-bound and Parallel Computation: a Historical Note // Oper. Res. Let., 7, 65-69, 1988.

19. Gomez S., Levy A.V. The Tunneling Method Applied to Global Optimization // SIAM, Numerical Optimization (Boggs, P.T., ed.), 213244, 1985.

20. Metropolis N., Rosenbluth A., Rosenbluth M., Teller A., Teller E. Equation of State Calculations by Fast Computing Machines // J. Chem. Phys. Vol. 21, No. 6, 1087-1092, 1953.

21. Aarts E.H.L., van Laarhoven PJ.M. Simulated Annealing: Theory and Applications // London, Kluwer, 1987.

22. АИ M., Storey C. Aspiration Based Simulated Annealing Algorithm // J. of Global Optimization 11, 181-191, 1996.

23. Hamma В., Viitanen S., A. Torn. Parallel Continuous Simulated Annealing for Global Optimization // Optimization Methods and Software, Vol. 13, №2, 93-116, 2000.

24. Michalewicz Z. Genetic Algorithms + Data Structures = Evolution Programs (3rd Edn.) // New York, Springer-Verlag, 1996.

25. Price W.L. A Controlled Random Search Procedure for Global Optimization // The Computer Journal, 20, 367-370, 1977.

26. AH M., Torn A., Viitanen S. A Numerical Comparison of Some Modified Controlled Random Search Algorithms // J. of Global Optimization 11, 377-385, 1997.

27. Rubinov A. Andramonov M. Lipschitz programming via increasing convex-along-rays functions // Optimization Methods and Software, 1999. V. 10. P. 763-781.

28. С.С.Кутателадзе, А.М.Рубинов. Двойственность Минковского и ее приложения. ~ Новосибирск: Наука, 1976.

29. Pallachke D., Rolewicz S. Foundations of Mathematical Optimization (Convex Analysis without Linearity). Kluwer Academic Publishers, Dordrecht, 1997.

30. Singer I. Abstract Convex Analysis. New York: Willey \& Sons, 1997.

31. A.M.Rubinov. Abstract Convexity and Global Optimization. Dordrecht, Kluwer Academic Publishers, 2000.

32. J. Kelley. The cutting plane method for solving convex programs // SIAM Journal, 1960. V. 8, № 4. P. 703-712.

33. Анциферов Е.Г., Ащепков Л.Е., Булатов В.П. Методы оптимизации и их приложения. 4.1. Математическое программирование. Новосибирск: Наука, 1990.

34. Хамисов О.В. Глобальная оптимизация функций с вогнутой минорантой // Журнал вычисл. математики и матем. физики. 2004. Т. 44. №9. С. 1552-1563.

35. А.Р.Ершов, О.В.Хамисов. Автоматическая глобальная оптимизация //. Дискретный анализ и исследование операций. 2004. Серия 2. T.l 1, № 2. С 45-68.

36. Евтушенко Ю.Г. Методы решения экстремальных задач и их применение в системах оптимизации. М.: Наука, 1982.

37. Гроссман К., Каплан А.А. Нелинейное программирование на основе без условной минимизации. Новосибирск: Наука, 1981.

38. Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации. М.: Наука, 1986.

39. D.D. Morrison, Optimization by least squares // SIAM J. Numer. Analysis, 1968. № 5. P. 83-88.

40. J. Kowalik, M.R. Osborn and D.M. Ryan, A new method for constrained optimization problems // Operat. Res., 1969. V. 17. P. 973-989.

41. Докл. АН СССР. 1967. Т.-173, №-4. С.-748-751. 46.Евтушенко Ю.Г., Жадан В.Г. Точные вспомогательные функции в задачах оптимизации // Журнал вычисл. матем. и матем. физики,1990. Т. 30. № 1. С.31-42.

42. Evtushenko Yu.G., Rubinov A.M. and Zhadan V.G. General Lagrangetype functions in constrained global optimization. Part II: Exact auxiliary functions // Optimization ' 48.Methods and Software, 2002. Vol. 16, № 1-4. P. 231-256.

43. A.M.Bagirov and A.M.Rubinov. Global minimization of increasing positively homogeneous functions over the unit simplex, Research Report 99/37, University of Ballarat, 1999.

44. Gourdine E., Jaumard В., Ellaia R. Global optimization of Holder functions // J. Global Optim. 1996. V.8, N 4. P.323-348.

45. Сухарев А.Г. Минимаксные алгоритмы в задачах численного анализа. М.: Наука, 1989.

46. Hansen P., Jaumard В., Lipschitz optimization // Handbook of global optimization. Dordrecht: Kluwer Acad. Publ., 1995. P. 407-494

47. Horst R., Nast M., Thoai N.Y. New LP bound in multivariable Lipschitz optimization: theory and applications // J. Optim. Theory Appl. 1995. V. 86, №2. P. 369-388

48. Pinter J. Global optimization in action. Dordrecht: Kluwer Acad. Publ., 1996.

49. Sergeev Ya.D. An one-dimensional deterministic global optimization algorithm. // Журн. вычисл. математики и матем. физики. 1995. Т. 35, №5. Р. 705-717

50. Wood G.R., Zhang В.Р. Estimation of the Lipschitz constant of a function // J. Global Optim. 1996. V.8, N 1. P. 91-103.

51. Baritompa W. Accelerations for a variety of global optimization methods // J. Global Optim. 1994. V.4, N 1. P. 37-45.

52. Breiman L., Cutler A. A deterministic algorithm for global optimization // Math. Program. 1993. V. 58, N 2, P. 179-199.

53. Gergel V.P. A global optimization algorithm for multivariable functions with Lipschitzian first derivatives // J. Global Optim. 1997. V.10, N 3. P. 257-281.

54. Коршунов Ю.М., Коршунов Ю.М. Математические основы кибернетики. — М.: Энергоатомиздат, 1972.Максимов Ю.А.,Филлиповская Е.А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.

55. Сухарев А.Г., Подобедов В.Е., Алгоритм поиска глобального максимума функции нескольких переменных. // Вычислительные комплексы и моделирование сложных систем. М.: МГУ, 1989. С. 124-134.

56. Брайсон А., Хо Ю-Ши. Прикладная теория оптимального управления

57. Шнитман В., Отказоустойчивые компьютеры компании Stratus // Открытые Системы № 1 1998

58. Дубова Н., Суперкомпьютеры nCube // Открытые Системы № 2 1995

59. Макстеник М., Сравнение сетевых архитектур // Сети № 2 1997

60. Французов Д., Оценка производительности вычислительных систем // Открытые Системы № 2 1996

61. Французов Д., Оценка производительности суперкомпьютеров // Открытые Системы № 6 19956 8. Воеводин В.В., Параллельная обработка данных, htlp://w\vw.parallel.ru/wv/

62. Комолкин A.B., Немнюгин С.А., Программирование для высокопроизводительных ЭВМ, http://vvww.hpc.nw.ru/COURSES/HPC/

63. Кркжов В.А., Операционные системы распределенных вычислительных систем (распределенные ОС), http://www.parallel.ru/krukov/

64. Ian Foster, Designing and Building Parallel Programs, http://rsusu 1 .rnd.runnet.ru/tutor/design/dbpp/text/book.html

65. Booth S., MacDonald N., Perfomance Optimization, http://www.hpc.nw.ru/COURSES/

66. Спыну С.К. Поиск глобального экстремума с использованием параллельных вычислений. Сб. трудов Международной НТК «XXX Гагаринские чтения», (Москва, 6-10 апреля 2004 г.). — М.: «МАТИ» -РГТУ им. К.Э.Циолковского, 2004, т.5, с.101

67. Спыну С.К. Поиск глобального экстремума с использованием параллельных вычислений. «Успехи современного естествознания» 2004, №7, с. 94,94.

68. Беневоленский Д.С., Жадан И.В., Спыну С.К. Использование параллельных вычислений при расчете метода половинных делений для глобальной оптимизации функции многих переменных. «Успехи современного естествознания» 2005, №7, с. 94,94.

69. Беневоленский Д.С., Жадан И.В., Спыну С.К. Виртуальная суперЭВМ на основе использования распределенных вычислений в локальной вычислительной сети для решения сложных научно-технических задач. «Успехи современного естествознания» 2005, №7, с. 94,94.

70. Беневоленский С.Б., Жадан В.Г., Жадан И.В., Истомина Н.Л., Спыну М.В., Спыну С.К. Принципы создания программного обеспечения для систем распределенного вычисления. «Успехи современного естествознания» 2005, №7, с. 94,94.

71. Свидетельство об отраслевой регистрации разработки №5383 «Программное обеспечение для поиска глобального экстремума функции многих переменных С1оЬех», Дата регистрации 16 ноября 2005г.

72. Беневоленский Д.С., Жадан В.Г., Жадан И.В. Технология вычислений в распределенной среде при расчете метода половинных делений для глобальной оптимизации функции многих переменных // Нейрокомпьютеры, 2007, 5, С. 8-11.

73. Свидетельство о государственной регистрации программы для ЭВМ №2009616922 «Программное обеспечение для поиска глобального экстремума методом половинных делений при неравномерном покрытии», Дата регистрации 14 декабря 2009г.

74. Беневоленский С.Б., Жадан И.В. Модификация метода половинных делений путем использования метода сопряженных градиентов. XXXV Гагаринские чтения: материалы Международной молодежной научной конференции в 8 томах, Москва, 2009, т.4, с. 7677.

75. MPI: The Message Passing Interface http://parallel.ru/tech/techdev/mpi.html.

76. Александр Каленюк, "Нестандартные алгоритмы сортировки".

77. Подбельский В.В. Язык Си++. М.: Финансы и статистика, 2000. -560с.

78. В. В. Воеводин, Вл. В. Воеводин, Параллельные вычисления. 2002, с.600

79. Корнеев В. В., Параллельные вычислительные системы. 1999, с.320

80. В.Ф.Кравченко, О.В.Лазаренко, В.И.Пустовойт, Л.Ф.Черногор. Вейвлет -анализ поведения солитонов при обгонном и обменном взаимодействиях. Доклады академии наук, 2007, том 412, №2 с. 179184.

81. Кравченко В.Ф., Пустовойт В.И., Чуриков Д.В. Цифровая обработка нелинейных сигналов на основе преобразования Кравченко-Котельникова Вигнера. Успехи современной радиоэлектроники. Зарубежная радиоэлектроника. 2007, №8, с.67-71.

www.dissercat.com

Жадан, Виталий Григорьевич - Методы оптимизации [Текст] : учебное пособие для студентов вузов по направлению подготовки "Прикладные математика и физика"

Поиск по определенным полям

author:иванов

Можно искать по нескольким полям одновременно:

author:иванов title:исследование

Логически операторы

исследование разработка

author:иванов title:разработка

оператор OR означает, что документ должен соответствовать одному из значений в группе:

исследование OR разработка

author:иванов OR title:разработка

оператор NOT исключает документы, содержащие данный элемент:

исследование NOT разработка

author:иванов NOT title:разработка

Тип поиска

$исследование $развития

Для поиска префикса нужно поставить звездочку после запроса:

исследование*

Для поиска фразы нужно заключить запрос в двойные кавычки:

"исследование и разработка"

Поиск по синонимам

#исследование

Группировка

author:(иванов OR петров) title:(исследование OR разработка)

Приблизительный поиск слова

Для приблизительного поиска нужно поставить тильду "~" в конце слова из фразы. Например:

бром~

бром~1

По умолчанию допускается 2 правки.

Критерий близости

"исследование разработка"~2

Релевантность выражений

исследование^4 разработка

По умолчанию, уровень равен 1. Допустимые значения - положительное вещественное число.

Поиск в интервале

author:[Иванов TO Петров]

author:{Иванов TO Петров}

search.rsl.ru

Диссертация на тему «Методы решения задач линейной оптимизации большой размерности» автореферат по специальности ВАК 01.01.09 - Дискретная математика и математическая кибернетика

1. Антипин А.С. Методы нелинейного программирования, основанные на прямой и двойственной модификации функции Лагранжа. М.: ВНИИСИ. 1979.

2. Булавский В.А., Звягина Р.А., Яковлева М.А. Численные методы линейного программирования. М.: Наука, 1977.

3. Вильчевский Н. О. О выборе коэффициента штрафа в задачах линейного программирования // Автомат, и телемехан. 1970. N 4. С. 121126.

4. Васильев Ф.П., Иваницкий А.Ю. Линейное программирование. М.: Факториал, 2003.

5. Гейл Д. Теория линейных экономических моделей. М.: Изд-во иностр. лит., 1963.

6. Голиков А.И., Евтушенко Ю.Г. Отыскание нормальных решений в задачах линейного программирования // Ж. вычисл. матем. и матем. физ. 2000. Т. 40. № 12. С. 1766-1786.

7. Голиков А.И., Евтушенко Ю.Г. Новый метод решения систем линейных равенств и неравенств // Докл. РАН. 2001. Т. 381. №4. С. 1-4.

8. Голиков А.И., Евтушенко Ю.Г. Теоремы об альтернативах и их применение в численных методах // Ж. вычисл. матем. и матем. физ. 2003. Т. 43. № 3. С. 354-375.

9. Голиков А.И., Евтушенко Ю.Г. Применение теорем об альтернативах к нахождению нормальных решений линейных систем // Изв. вузов. Математика. 2001. №12 (475). С. 21-31.

10. Голиков А.И., Евтушенко Ю.Г., Кетабчи С. О семействах гиперплоскостей, разделяющих полиэдры // Ж. вычисл. матем. и матем. физ. 2005. Т. 45. № 2. С. 238-253.

11. Голиков А.И., Евтушенко Ю.Г, Моллаверди Н. Применение метода Ньютона к решению задач линейного программирования большой размерности // Ж. вычисл. матем. и матем. физ. 2004. Т. 44. № 9. С. 1564-1573.

12. Голынтейн Е.Г., Третьяков Н.В. Модифицированные функции Лагранжа, теория и методы оптимизации. М.: Наука, 1989.

13. Голынтейн Е.Г., Юдин Д.Б. Новые направления в линейном программировании. М.: Сов.радио, 1966.

14. Евтушенко Ю. Г., Жадан В. Г. Численные методы решения некоторых задач исследования операций // Ж. вычисл. матем. и матем. физ. 1973. Т. 13. N. 3. С. 583-597.

15. Евтушенко Ю. Г. Два численных метода решения задач нелинейного программирования // Докл. АН СССР. 1974. Т. 215. N. 1. С. 38-40.

16. Евтушенко Ю. Г., Жадан В. Г. Релаксационный метод решения задач нелинейного программирования // Ж. вычисл. матем. и матем. физ. 1977. Т. 17. N. 4. С. 890-904.

17. Евтушенко Ю. Г., Жадан В. Г. Барьерно-проективные и баръерно-ньтоновские численные методы оптимизации (случай линейного программирования) . М.: ВЦ РАН, 1992.

18. Еремин И.И. Теория линейной оптимизации. Екатеринбург: УрО РАН, 1998.

19. Еремин И. И., Астафьев Н. Н. Введение в теорию линейного и выпуклого программирования. М.: Наука, 1976.

20. Еремин И.И., Мазуров В.Д., Астафьев Н.Н. Несобственные задачи линейного и выпуклого программирования. М.: Наука, 1983.

21. Еремин И.И. Противоречивые модели оптимального планирования. М.: Наука, 1983.

22. Еремин И.И. Двойственность в линейной оптимизации. Екатеринбург: УрО РАН, 2001.

23. Еремин И.И. О квадратичных задачах и полноквадратичных задачах выпуклого программирования // Известия вузов. Матем. 1998. № 12. С. 22-28.

24. Дикин И. И. Итеративное решегьие задач линейного и квадратичного программирования // Докл. АН СССР. 1967. Т. 174. N. 4. С. 745-747.

25. Кутанов А. Т. Об уточнении решения задачи линейного программирования в методе штрафных функций // Автомат, и телемехан. 1970. N 4. С. 127-132.

26. Линейные неравенства и смео/сные вопросы. // Сб. работ под ред. Куна Г. и Таккера А. М.: ИЛ. 1959.

27. Моллаверди Н. Решение систем линейных равенств и неравенств большой размерности. Тезисы докладов конференции "Алгоритмический анализ неустойчивых задач", Екатеринбург, 2004, с.287

28. Моллаверди Н., Тюленев А.В. О программной реализации нового метода решения задач линейного программирования. Тезисы докладов конференции "Математическое программирование и приложения", Екатеринбург, 2003, с.185.

29. Муртаф Б. Современное линейное программирование. М.: Мир, 1984.

30. Поляк Б.Т. Введение в оптимизацию. М.: Наука, 1983.

31. Поляк Б.Т., Третьяков Н.В. Об одном итерационном методе линейного программирования и его экономической интерпретации // Эконом, и матем. методы. 1972. Т. VIII. Вып. 5.

32. Пропой А. И., Ядыкин А. Б. Параметрическое квадратичное программирование и линейное программирование II j j Автомат, и телемехан. 1978. N 2. С. 102-112, N 4. С. 135-143.

33. Разумихин Б.С. Физические модели и методы теории равновесия в программировании и экономике. М.: Наука, 1975.

34. Разумихин Б. С. О двух методах условной оптимизации II. Метод годографа для задач линейного программирования// Модели и методы оптимизации. Тр. ВНИИСИ. N 3. М.: ВНИИСИ, 1980. С. 37-53.

35. Рапопорт JI. Б. Модифицированый метод годографа для задач линейного программирования // Модели и методы оптимизации. Тр. ВНИИСИ. N 3. М.: ВНИИСИ, 1980. С. 82-93.

36. Схрейвер А. Теория линейного и целочисленного программирования. М.: Мир, 1991.

37. Тихонов А.Н.Избранные труды. М.: МАКС Пресс, 2001.

38. Тихонов А. Н., Арсеиин В. Я. Методы решения некорректных задач. М.: Наука, 1979.

39. Удзава X. Итерационные методы вогнутого программирования // К. Дж. Эрроу, J1. Гурвиц, X. Удзава. Исследования по линейному и нелинейному программированию. М.: Изд-во иностр. лит., 1962. С. 228-245.

40. Фиакко А., Мак-Кормик Г. Нелинейное программирование. Методы последовательной безусловной минимизации. М.: Мир, 1972.

41. Чеботарев С. П. Об изменении коэффициента штрафа в задачах линейного программирования // Автомат, и телемехан. 1974. N 3. С. 102-107.

42. Черников С.Н. Линейные неравенства. М.: Наука, 1968.

43. Юдин Д.Б., Голыптейн Е.Г. Линейное программирование: теория, методы и приложения. М.: Наука, 1969.

44. Ядыкип А. Б. О параметризации в вырожденных задачах квадратичного программирования // Ж. вычисл. матем. и матем. физ. 1977. N 3. С. 634-648.

45. Evtushenko Yu. Computational of exact gradients in disributed dynamic systems // Optimiz. Meth. and Software. 1998. V. 9. № 1-3. Pp. 45-75.

46. Evtushenko Yu.G., Golikov A.I. New perspective on the theorems of alternative // High Performance Algorithms and Software for Nonlinear Optimization. Kluwer, 2003. Pp. 227-241.

47. Evtushenko Yu.G., Golikov A.I., Ketabchi S., Mollaverdi N. Augmented Lagrangin method for linear programming // Dynamics of non-homogeneous systems. M.: Russian Academy of Sciences Institute for System Analysis. 2004. V. 7. Pp. 101-106.

48. Evtushenko Yu. G., Moretti A., Zhadan V. G. Newton's steepest descent for linear programming // Dynamics of non-homogeneous systems. Proceedings of ISA RAS. V. 2. M.: Editorial URSS. 1999. P. 86-108.

49. Evtushenko Yu. G., Zhadan V. G. Space-transformation technique: the state of the art. // Nonlinear Optimization and Applications (Edited by G. DI Pillo, F. Giannessi). Kluwer Acad. Publis. 1996. P. 101-123.

50. Kanzow C., Qi H., Qi L. On the Minimum Norm Solution of Linear Programs // Journal of Optimization Theory and Applications. 2003. V. 116. Pp. 333-345.

51. Karmarcar N. A new polinomial-time algorithm for linear programming // Combinatorica. 1984. N 4. P. 373-395.

52. Mangasarian O. L., Meyer R. R. Nonlinear perturbation of linear programs// SIAM J. Control and Optimizat. 1979. V. 17. N 6. P. 745-752.

53. Mangasarian О. L. Normal solutions of linear programs // Math. Program. Study. 1984. V. 22. P. 206-216.

54. Mangasarian O. L. Least-norm linear programming solution as an unconstrained minimization problem // J. Math. Analysis and Applic. 1983. V. 92. P. 240-251.

55. Mangasarian O.L. Nonlinear programming. Philadelphia: SIAM, 1994.

56. Mangasarian O.L. A Finite Newton Method for Classification // Optimizat. Meth. and Software. 2002. V. 17. Pp. 913-930.

57. Mangasarian O.L. A Newton Method for Linear Programming // Journal of Optimization Theory and Applications. 2004 121. pp. 1-18.

58. Meszaros Cs.( The BPMPD interior point solver for convex quadratic programming problems. // Optimizat. Meth. and Software. 1999.11&12,

59. Roos C., Terlaky Т., Vial J.-Ph. Theory and algorithms for linear optimization. An interior point approach. Chichester: John Wiley & Sons,

60. Special issue on interior point methods // Optimizat. Methods &431.449.1997.

61. Software. 1999. V. 11. N 1-4. P. 1-690.

www.dissercat.com

Диссертация на тему «Методы неравномерных покрытий и их применение для решения задач глобальной оптимизации в диалоговом режиме» автореферат по специальности ВАК 05.13.02 - Теория систем, теория автоматического регулирования и управления, системный анализ

1. Моисеев Н.Н. Математические задачи системного анализа. - М., Наука, 1981, 488с.

2. Стронгин Р.Г. Численные методы в многоэкстремальных задачах. -М., Наука, 1978, 240с.

3. Dixon L. С. V/., Gomulka J.,Szego G.P. Towards a Global Optimization Technique. In: Towards Global Optimization. Dixon L.C.W., Szego G.P. ( Ed.)., Amsterdam, Oxford, North-Holland Publ.Co., New-York, Amer. Elsevier Publ.Co. Inc., 1975, pp. 29-54 .

4. Моцкус Й.Б. Многоэкстремальные задачи в проектировании. М., Наука, 1967, 215с.7. -Растригин Л.А. Система экстремального поиска. М., Наука, 1974, 630с.

5. Глушков В.М. О диалоговом методе решения оптимизационных задач. Кибернетика, 1975, № 4, с. 2-6.

6. Поспелов Г.С. Искусственный интеллект. Новая информационная технология. Веетн.Академии наук СССР, 1983, № 8, с.31-42.

7. Ю.Евтушенко Ю.Г. Методы решения экстремальных задач и их применение в системах оптимизации. М., Наука, 1982, 432с.

8. Евтушенко Ю.Г. Методы поиска глобального экстремума, В кн.: Исследование операций (модели, системы, решения). Вып. 4, М.,изд—во ВЦ АН СССР, 1974, с. 39-68.

9. Пиявский С.А, Алгоритм отыскания абсолютного минимума функций.- В кн.: Теория оптимальных решений. Вып, 2, Киев, изд-во ИК АН УССР, 1967, с.13-24.

10. Данилин Ю.М., Пиявский С.А. Об одном алгоритме отыскания абсолютного миницума. В кн.: Теория оптимальных решений. Вып. 2, Киев, изд-во ИК АН УССР, 1967, с. 25-37.

11. Пиявский С.А. Один алгоритм отыскания абсолютного экстремума функции. Журнал вычисл.матем. и матем.физ., 1972, т. 12,4, с. 888-896.

12. Васильев Ф.П. Численные методы решения экстремальных задач. -М., Наука, 1980, 520с.

13. Черноусько Ф.Л. Об оптимальном поиске экстремума унимодальных функций. Журнал вычисл. матем. и матем. физ. 1970, 10, № 4, с. 922-933.

14. Сухарев А.Г. Наилучшие стратегии последовательного поиска экс-стремума. Журнал вычисл.матем. и матем. физ., 1972, 12, № I, с. 35-50.

15. Евтушенко Ю.Г. Численный метод поиска глобального экстремума.- Журнал вычисл. матем. и матем. физ., 1971, т, II, № 6, с. 1390-1403.

16. Минков И.М. Об определении глобального минимума в задаче синтеза тонкослойных покрытий. Оптика и спектроскопия, 1981, т. 50, вып. 54, с. 755-766.

17. Бурдаков О.П., Веселов Е.Н., Голиков А.И., Грачев Н.И., Евтушенко Ю.Г., Жадан В.Г., Мазурик В.П., Потапов М.А. Диалоговый комплекс программ ДИСО. Постановка задач на процедурном уровне. Деп. в ВИНИТИ № 2715-82 ДЕЛ., 1982 , 39с.

18. Евтушенко Ю.Г., Бурдаков О.П., Грачев Н.И., Жадан В.Г., Потапов М.А. Диалоговый комплекс программ ДИСО. Раздел безусловной минимизации. Дп. в ВИНИТИ № 2717-82 ДЕП., 1982, 98с.

19. Евтушенко Ю.Г., Бурдаков О.П., Голиков А.И., Мадан В.Г., Потапов М.А. Диалоговый комплекс программ ДИСО. Раздел нелинейного программирования. Деп. в ВИНИТИ № 2716-82 ДЕП., 1982, 87с.

20. Потапов М.А. Пакет методов глобального поиска для диалоговой системы оптимизации (ДИСО). В кн.: Пакеты прикладных программ. Методы оптимизации. М.: Наука, 1984, с. 84-92.

21. Веселов Е.Н. Инструментальная система для построения диалоговых пакетов программ. Автореф. дис. . канд.физ.-мат.наук, М., 1980, 16с.

22. Веселов Е.Н., Мазурик В.П. Инструментальные средства для проблемно-ориентированных систем. В кн.: Проблемы вычислительной техники, М., изд-во МЩТИ, 1981, с. 123-144.

23. Васильев Н.С. К отысканию глобального минимума квазивогнутой функции. Журнал вычисл. матем. и матем. физ., 1983, т. 23, № 2, с. 307-313.

24. Рейнгольд Э., Нивергелы?Ю., Део Н. Комбинаторные алгоритмы (теория и практика). М., Мир, 1980, 478с.

25. Лучанская Х.И., Хевролин В.Я. Решение задачи Л.И.Мандельштама. Радиотехника, 1974, т. 29, № 12, с. 1-5.

26. Потапов М.А. Модифицированный метод прямого поиска. В кн.: Исследование операций (модели, системы, решения). Вып. 7. -М., изд-во ВЦ АН СССР, 1979, с. II5-I20.

27. Краснощеков П.С., Морозов В.В., Федоров В.В. Декомпозиция в задачах проектирования. Изв. АН СССР, сер. Технич.киберн., 1979, № 2, с. 7-17.

28. Дмитровский А.Е., Попов Н.М. Некоторые математические вопросы формирования облика сложной технической системы на этапе предварительного проектирования. В кн.: Автоматизация проектных и конструкторских работ., М., 1979, с. 55-57.

29. Соболь И.М., Статников Р.Б. Выбор оптимальных параметров в задачах со многими критериями. М., Наука, 1981, 110с.

30. Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач. М., Наука, 1982, 256с.

31. Поспелов Г.С., Ириков В.А. Программно-целевое планирование и управление. - М., Сов.радио, 1976, 246с.

32. Гермейер Ю.Б. Введение в теорию исследования операций. М., Наука, 1971, 384с.

33. Подиновский В.В. Методы много1фитериальной оптимизации. Вып.1, Эффективные планы. М., 1971, 118с.

34. Гергель В.П. Решение одного класса многомерных многоэкстремальных многокритериальных задач со сложными ограничениями. Авто-реф. дис. . канд.техн.наук, Горький, 1984, 18с.

35. Попов Н.М. Об аппроксимации множества Парето методом сверток. -Вестник Моск. ун-та, Сер. Вычисл. матем. и киберн., 1982, № 2, с. 35-41.

36. Молодцов Д.А. Регуляризация множества точек Парето, Журнал вычисл. матем. и матем. физ., 1978, т. 18, № 3, с, 597-602.

37. Молодцов Д.А., Федоров В.В. Устойчивость принципов оптимальности. В кн.: Современное состояние теории исследования операций. - М., Наука, 1979, с. 236-262.

38. Попов Н.М. Аппроксимация много1фитериальных задач в проектировании. Автореф. дис. . канд. физ.-матем.наук, М., 1983, 18с.

39. Сухарев А.П. Об оптимальных методах решения многокритериальных задач. Изв. АН СССР, сер. Технич.киберн., 1982, № 3, с.67-73.

40. Потапов М.А. Об одном мето^де решения многокритериальных задач проектирования. В кн.: Автоматизация проектирования и конструирования. М., ч. I, 1983, с. 43-44.

41. Evtushenko Y., Potapov М. Space covering technique for multi-criterion optimization. In: Lecture Notes in Control and Information Sciences , 1984, Vol. 59, pp. 201-202 .

42. Evtushenko Y., Potapov M. Non-differentiable approach to multicriterion optimization. In: Nondifferentiable Optimization. Motivations and Applications.,IIASA, Laxenburg,1984i43-45.

43. Тихонов A.M., Арсенин В.Я. Методы решения некорректных задач. -М., Наука, 1974, 222с.49^ Глушков В.М. О системной оптимизации. Кибернетика, 1980, № 5, с. 89-90.

44. Кахро М.И., Калья А.П., Тыугу Э.Х. Инструментальная система программирования ЕС ЭВМ (ПРИЗ). М., Финансы и статистика, 1981, 158с.

45. Глушков В.М., Олеярш Г.Б. Диалоговая система планирования ДИСПЛАН. Управляющие системы и машины, 1976, № 4, с.123-124.

46. Глушков В.М. и др. Автоматизацияя проектирования вычислительных машин. Киев, Наукова думка, 1975, 231с.

47. Родин C.P., Эрлих А.И. Интерактивные системы блочного моделирования. В кн.: Вопросы информационной теории и практики,46, М., ВИНИТИ, 1981, с. 67-73.

48. Михалевич B.C., Сергиенко И.В. и др. Пакет прикладных программ ДИСПРО, предназначенный для решения задач дис1фетного программирования. Кибернетика, 1981, № 3, с.I17-137.

49. Гуляницкий Л.Ф., Сергиенко И.В. О пакете прикладных программ ВЕКТОР-2 для решения задач комбинаторной оптимизации. В кн.: Пакеты прикладных программ. Методы оптимизации, М., Наука, 1984, с. 59-65.

50. Михалевич B.C., Сергиенко И.В. и др. Пакет : прикладных программ для решения задач производственно-транспортного планирования большой размерности. В кн.: Пакеты прикладных программ. Методы оптимизации, М., Наука, 1984, с. 66-84.

51. Веселов Е.Н., Евтушенко Ю.Г., Мазурик В.П. Содержательные возможности диалоговой системы оптимизации (ДЙСО). В кн.: Проблемы вычислительной техники, М., изд-во МЦНТИ, 1981, с.110-122.

52. Веселов Е.Н., Мазурик В.П. Диалоговая система оптимизации (инструкция пользователю). М., Изд-во ВЦ АН СССР, 1980, 56с.60 •Brooks S.H. A Discussion of Random Methods for Seeking Maxima. Operations Res., 1952, Vol. 6, N 2, pp.244-251.

53. Соболь И.М. Численные методы Монте-Карло. M.t Наука, 1973, 2I2c.

54. Гришагин В.А. Алгоритм оцределения экстремальных значений функции нескольких переменных. Алгоритмы и программы. Информационный бюллетень. - М.: ВНТИЦ, 1978, № 6, с. 64.

55. Гришагин В.А. Программная реализация многошаговых алгоритмов глобального поиска. В сб.: Математическое обеспечение САПР. - Горький: изд. ГГУ, 1981, с. 150 - 163.

56. Гришагин В.А. Программа вычисления абсолютного экстремума, минимаксов и максиминов функции нескольких переменных (АЛГОЛ-БЭСМ-6). Алгоритмы и программы. Информационный бюллетень. -М.; ВНИТЦ, 1979, № 5, с. 21.

57. Гришагин В.А. Операционные характеристики некоторых алгоритмов глобального поиска. Вып. 7. Рига, Зинатне, 1978, с. 198-206.

58. Гришагин В.А. Экспериментальное сопоставление нескольких алгоритмов глобального поиска. В сб.: Автоматизированное и оптимальное проектирование. - Горький: изд. ГГУ, 1977, с.57-60.

59. Гришагин В.А. О выборе параметра в информационно-статистическом алгоритме глобального поиска. В сб.: Тезисы докладов Ш Всесоюзной конференции по исследованию операций. - Горький: изд. ГГУ, 1978, с. 313-314.

60. Гришагин В.А. Об условиях сходимости для одного класса алгоритмов глобального поиска. В сб.: Тезисы докладов Ш Всесоюзного семинара "Численные методы нелинейного программирования". -Харьков: изд. ХГУ, 1979, с. 82-84.

61. Brent R.P. Algorithms for minimization without derivatives.

62. Englewood Cliffs N.J., Prentice-Hall,1973, pp. 81-115.

63. Глориозов E.A., Ссорин В.Г., Сыпчук П.П. Введение в автоматизацию схемотехнического цроектирования. M.t Сов.радио, 1976, 224с.

64. Норенков И.П. Введение в автоматизированное проектирование технических устройств и систем. М., Высшая школа, 1980, 311с.

65. Чуа Л.О., Пен-Мин Лин. Машинный анализ электронных схем (алгоритмы и вычислительные методы). М., Энергия, 1980, 640с.

66. Евстифеев Ю.А., Фуке В.Й., Резников А.А., Селиванов А.В. Расчет параметров схемы замещения диода ^по модели Эберса-Молла с помощью ЭВМ. В кн.: Конструирование и технология изготовления космических приборов, М., Наука, 1983, с. 104-108.

67. Бэллман Р., Калаба Р. Квазилинеаризация и нелинейные краевые задачи. М., Мир, 1968, 183с.

68. Ильин В.Н. Основы автоматизации схемотехнического проектирования. М., Энергия, 1979, 392с.

69. Вязгин В.А. О синтезе критериев качества для задачи оптимизации параметров самолета. В кн.: Методы выбора рациональных цроектно-конструкторских решений в процессе создания самолетов, М., Изд-во МАИ, 1982, с. 10-18.

70. Остославский И.В., Стражева И.В. Динамика полета. Траектории летательных аппаратов. М., Машиностроение, 1969, 499с.

71. Миеле А. Механика полета, т. I. М., Наука, 1965, 407с.

72. Лебедев А.А., Чернобровкин Л.С. Динамика полета. М., Машиностроение, 1973, 452с.

73. Бадягин А.А., Егер С.М., Мишин В.Ф., Склянский Ф.И., Фомин Е.А, Проектирование самолетов. М., Машиностроение, 1972, 516с.

74. Югов О.И., Селиванов О,Д. Согласование характеристик самолета и двигателя. М., Машиностроение, 1975, 204с.

75. Пышнов B.C. Динамические свойства самолетов. М., Оборонгиз, 1951, 257с.