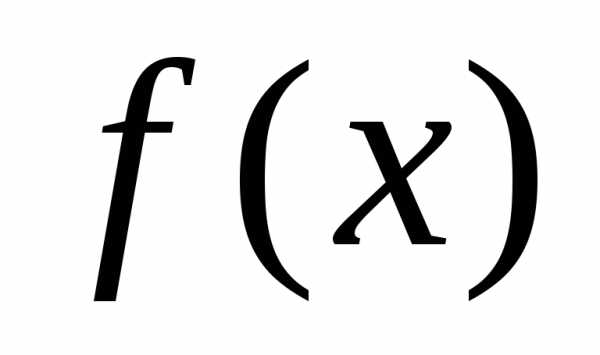Лабораторная работа 7. Исследование методов безусловной оптимизации первого порядка. Оптимизация лабораторная работа
Лабораторная работа № 4 Оптимизация сроков выполнения кпп
Цель работы: Календарное планирование КПП на основе построения сетевого графика и его оптимизации с целью соблюдения директивных сроков выполнения КПП.
Используемое программное обеспечение- ППП «prima» (сетевой график), программаExcel. Системные требования: операционная системаWindows2000,Windows98; процессорIntelPentiumШ 600 мГц, оперативная память 128 Мб
Методические указания
На основе типового перечня этапов выполнения КПП и распределения трудоемкости по отдельным работам и профессиональным группам (л. р. N 3) следует расчленить процесс разработки КПП на отдельные события и работы и определить последовательность и сроки выполнения всех работ и наступления событий.
При построении сетевого графика и в дальнейших расчетах необходимо учесть следующее:
1. В связи с отсутствием опробированных конструкторских решений, удовлетворяющих предъявляемым требованиям, возникает необходимость применить в проектируемом изделии новый принцип, требующий теоретической разработки и прикладных исследований (НИР), которые должны быть завершены до начала разработки технического предложения.
2. Эскизный проект включает выполнение оценки экономической эффективности конструкции нового изделия, которая производится экономическими службами предприятия.
3. Ставится задача обеспечить превышение параметров, достигнутых в предшествующих конструкциях. Возникает необходимость в проведении экспериментальных работ, связанных с проверкой новых параметров машины.
4. Перед разработкой технического проекта эскизный проект должен быть утвержден заказчиком.
5. Е связи с применением новых принципов возникает необходимость внесения изменений в конструкцию отдельных деталей и в проверке функционирования изделия в условиях, приближенных к эксплуатационным.
Все вышеуказанные работы выполняются за рамками конструкторского бюро, поэтому длительность их выполнения регулировать нет возможности.
Длительность остальных работ КПП зависит от количества исполнителей - работников КБ, что следует учитывать при оптимизации сетевого графика. Длительность выполнения каждой работы зависит от трудоемкости работы по каждой группе исполнителей и их количества.
(20),
где tij- длительность работы в календарных днях;
tрб- трудоемкость отдельных работ, чел-ч;
tсрд- средняя продолжительность рабочего дня.ч;
р - количество исполнителей, одновременно выполняющих данную работу, чел.;
Кпер- коэффициент перевода рабочих дней в календарные
(21),
Дк.год- количество календарных дней в году;
Др.год- количество рабочих дней за тот же период.
Расчет длительности выполнения работ по КПП, выполняется в табл. 11.
Оптимизация сетевого графика состоит в максимально возможном сокращении критического пути сетевого графика за счет перераспределения исполнителей. Практически эта задача сводится к сокращению критического пути до заданного директивного срока.
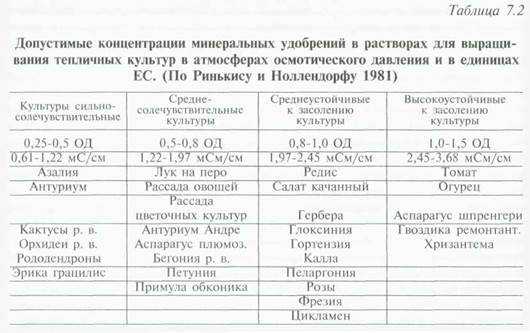
Таблица 11 - Перечень работ сетевого графика
| № работы | Краткое название | Цифровой код работы i-j | Трудоемкость чел-дни tрб | Число исполнителей, чел. р | Продолжительность, дни tij |
| НИР Техническое задание Обработка результатов НИР Эксперимент Оценка экономической эффективности Техническое предложение Фиктивная работа Фиктивная работа Эскизный проект Оценка у заказчика Технический проект Рабочая документация Испытание опытного образца Фиктивная работа | 1-2 1-3 2-3 3-4 3-5 3-6 4-6 5-6 6-7 7-8 8-9 9-10 9-11 10-11 | * * * * * * * * | * * * * * * * * | 90 5 14 3 0 0 3 0 |
Календарные сроки выполнения КПП определяются на ЭВМ и сводятся в табл. 12.
Таблица 12 - Календарные сроки выполнения КПП
| Этапы КПП | Календарные даты работы | |
| Начало | Окончание | |
В отчете о работе необходимо привести табл. 11, данные и календарные сроки выполнения работ в форме табл. 12.
studfiles.net
Лабораторная работа №3 "Методы оптимизации первого и второго порядков"
страница 1 Лабораторная работа №3 “Методы оптимизации первого и второго порядков”Задание для лабораторной работы
- Написать условие задачи и аналитическое выражение для градиента.
- Решить задачу методом Коши, используя различные методы нахождения шага: метод квадратичной интерполяции, метод кубической интерполяции и метод первого приемлемого значения.
- Решить задачу методами Флетчера-Ривса и Полака-Рибьера.
- Решить задачу методами DFP и BFGS.
- Решить задачу методами Ньютона-Рафсона и Марквардта.
- Представить результаты решения задачи различными методами в таблице.
- Сделать выводы о влиянии способа отыскания шага на ход решения задачи.
- Сравнить результаты, полученные методами первого порядка, методами переменной метрики и методами второго порядка.
- Реализовать один из методов оптимизации в соответствии с вариантом, (см. таблицу 5). Проверить работу реализованного метода на квадратичной функции (функция вида ) и функции Розенброка (функция вида ).
- Титульный лист.
- Задание.
- Уравнение функции, подлежащей минимизации.
- Аналитическое выражение градиента.
- График поверхности минимизируемой функции
- Графики линий уровня функции с указанными на них траекториями минимизации всеми методами первого и второго порядка.
- Таблица результатов минимизации функции вышеперечисленными методами.
- Выводы о траекториях минимизации полученными различными методами.
- Текст программы реализующей один из методов оптимизации.
- Результаты оптимизации квадратичной функции и функции Розенброка реализованным методом.
- Для сравнения на линиях уровня квадратичной функции и функции Розенброка указать траектории оптимизации, полученные с помощью собственной программы и с помощью предложенной программы.
- Математическая модель задачи безусловной оптимизации.
- Аффинная модель функции многих переменных
- Квадратичная модель функции многих переменных.
- Метод Коши.
- Метод Флетчера-Ривса.
- Метод Полака-Рибьера.
- Методы DFP и BFGS.
- Методы Ньютона, Ньютона-Рафсона, Марквардта.
- Методы нахождения шага: метод первого приемлемого значения, квадратичная интерполяция, кубическая интерполяция.
- Методы нахождения градиента: численный расчет градиента, вычисление градиента с помощью метода быстрого дифференцирования.
Задача №1
Студенту специальности АС дали задание сравнить результаты минимизации функции Розенброка различными методами прямого поиска.
Функция имеет вид: .
Данные для задачи представлены в таблице 1.
Задача №2
Водный инспектор получил задание поставить опознавательный знак на самом глубоком месте некоего водоема. Площадь водоема представляет собой систему координат. Известно, что дно водоема на всей его площади может быть описано следующей функцией , указывающей глубину в метрах над уровнем моря. Найти координаты места, в котором инспектору необходимо поставить этот опознавательный знак.
Данные для задачи представлены в таблице 2.
Задача №3
1-ое тело движется по траектории вида: , 2-ое по траектории вида: . Найти наименьшее расстояние между траекториями движения тел. Т.е. необходимо решить задачу:
найти min
Данные для задачи приведены в таблице 3.
Задача №4
Эллиптический параболоид и плоскость пересекаются в точке . Определить будет ли данная точка точкой минимума этого параболоида:
.
Данные для задачи приведены в таблице 4.
Таблица 1
| № | a | b | № | a | b |
| 1 | 100 | 1 | 11 | 50 | 1 |
| 2 | 90 | 2 | 12 | 60 | 2 |
| 3 | 110 | 3 | 13 | 171 | 6 |
| 4 | 120 | 1 | 14 | 160 | 2 |
| 5 | 80 | 4 | 15 | 90 | 5 |
| 6 | 90 | 2 | 16 | 110 | 1 |
| 7 | 100 | 3 | 17 | 80 | 2 |
| 8 | 150 | 4 | 18 | 95 | 3 |
| 9 | 145 | 5 | 19 | 100 | 4 |
| 10 | 75 | 1 | 20 | 115 | 2 |
| № | a | b | № | a | b |
| 1 | 1 | 2 | 11 | 3 | 1 |
| 2 | 1 | 3 | 12 | 3 | 2 |
| 1 | 4 | 13 | 3 | 3 | |
| 4 | 1 | 5 | 14 | 3 | 4 |
| 5 | 1 | 6 | 15 | 3 | 5 |
| 6 | 2 | 1 | 16 | 4 | 1 |
| 7 | 2 | 2 | 17 | 4 | 2 |
| 8 | 2 | 3 | 18 | 4 | 3 |
| 9 | 2 | 4 | 19 | 4 | 4 |
| 10 | 2 | 5 | 20 | 5 | 1 |
| № | а | b | № | а | b |
| 1 | 4 | 3 | 11 | 3 | 17 |
| 2 | 2 | 5 | 12 | 20 | |
| 3 | 6 | -4 | 13 | 1 | 3 |
| 4 | 6 | 12 | 14 | 4 | 2 |
| 5 | -5 | 3 | 15 | 11 | 2 |
| 6 | 0 | 5 | 16 | 4 | 3 |
| 7 | -3 | -6 | 17 | 2 | 5 |
| 8 | 8 | 8 | 18 | 6 | -4 |
| 9 | 5 | 5 | 19 | 0 | 1 |
| 10 | 4 | 6 | 20 | 6 | 12 |
| № | p | q | № | p | q |
| 1 | 3 | 1 | 11 | 6 | 7 |
| 2 | 4 | 0 | 12 | 23 | -8 |
| 3 | 8 | -5 | 13 | 3 | 5 |
| 4 | 3 | 14 | 14 | 2 | -9 |
| 5 | -8 | 5 | 15 | 12 | 2 |
| 6 | 0 | 5 | 16 | 18 | 2 |
| 7 | -3 | -2 | 17 | 5 | 4 |
| 8 | 5 | 8 | 18 | 7 | -1 |
| 9 | 8 | 5 | 19 | 9 | 3 |
| 10 | -4 | 6 | 20 | 6 | 0 |
| № | Метод поиска направления | Метод поиска шага |
| 1 | Метод Коши | Метод квадратичной интерполяции |
| 2 | Метод Флетчера-Ривса | Метод квадратичной интерполяции |
| 3 | Метод Полака-Рибьера | Метод квадратичной интерполяции |
| 4 | Метод DFP | Метод квадратичной интерполяции |
| 5 | Метод BFGS | Метод квадратичной интерполяции |
| 6 | Метод Ньютона-Рафсона | Метод квадратичной интерполяции |
| 7 | Метод Марквардта | |
| 8 | Метод Коши | Метод кубической интерполяции |
| 9 | Метод Флетчера-Ривса | Метод кубической интерполяции |
| 10 | Метод Полака-Рибьера | Метод кубической интерполяции |
| 11 | Метод DFP | Метод кубической интерполяции |
| 12 | Метод BFGS | Метод кубической интерполяции |
| 13 | Метод Ньютона-Рафсона | Метод кубической интерполяции |
| 14 | Метод Коши | Метод первого приемлемого значения |
| 15 | Метод Флетчера-Ривса | Метод первого приемлемого значения |
| 16 | Метод Полака-Рибьера | Метод первого приемлемого значения |
| 17 | Метод DFP | Метод первого приемлемого значения |
| 18 | Метод BFGS | Метод первого приемлемого значения |
| 19 | Метод Ньютона-Рафсона | Метод первого приемлемого значения |
- Постановка задачи
где является целевой функцией. При решении этой задачи используются методы минимизации, которые приводят к стационарной точке , определяемой уравнением . Данные методы используют первую и вторую частные производные.
Независимо от метода используют следующие условия останова:
- Достигнута заданная точность градиента: , где - малое положительное число.
- Проведено заданное количество итераций: , где - заданное количество итераций.
- Изменение значения функции и изменение вектора координат слишком мало: и , где - малое положительное число.
- Методы первого порядка
Градиентные методы носят итерационный характер и имеют единую модельную схему. Имея текущее приближение на k-ой итерации, выполняется последовательность следующих шагов:
Шаг 1. Проверка соблюдения условия остановки. Если условие выполняется, то вычисления прекратить и взять в качестве искомого решения, иначе перейти к Шагу 2.
Шаг 2. Расчет направления поиска .
Шаг 3. Расчет длины шага , обеспечивающее выполнение неравенства: .
Шаг 4. Пересчет оценки решения. Положить . Положить . Перейти на Шаг 1.
Способы определения достаточно хорошо отработаны и гарантируют убывание функции . Главной частью алгоритмов оптимизации является расчет направления . Для того чтобы был направлением минимизации функции , обычно контролируется выполнение условия
(4.1)
Метод Коши (метод наискорейшего спуска)
Применение метода наискорейшего спуска для решения задачи минимизации без ограничений было рассмотрено еще французским математиком Коши. Градиент целевой функции в любой точке есть вектор в направлении наибольшего локального увеличения . Следовательно, нужно двигаться в направлении, противоположном , т. е. в направлении наискорейшего спуска, поскольку отрицательный градиент в точке направлен в сторону наибольшего уменьшения по всем компонентам x и ортогонален линии уровня в точке . Введение направления, противоположного нормированному (единичному) градиенту , т. е. направления наискорейшего спуска, определяемого в точке по формуле
(4.2)
в дает следующую формулу перехода из в :
(4.3)
Отрицательный градиент дает только направление оптимизации, но не величину шага. При этом можно использовать различные процедуры метода наискорейшего спуска в зависимости от выбора и определения выражения . Поскольку один шаг в направлении наискорейшего спуска не приводит в точку минимума , формула (4.3) должна применяться несколько раз, до тех пор пока не будет достигнут минимум. В точке минимума все составляющие вектора градиента равны нулю.
При выборе размера шага применяются два общих метода. В первом методе при переходе из точки в точку целевая функция минимизируется по , в другом методе выбирается фиксированный или меняется от шага к шагу.
Метод Флетчера-Ривза
В методе сопряженного градиента Флетчера-Ривза строится последовательность направлений поиска s являющихся линейными комбинациями , текущего направления наискорейшего спуска, и , предыдущих направлений поиска, причем весовые коэффициенты выбираются так, чтобы сделать направления поиска сопряженными. Упомянутые веса такие, что для вычисления нового направления поиска в точке используется только текущий и предпоследний градиент.
Ниже приводятся операции этого алгоритма:
Шаг 1. В вычисляется
.
Шаг 2. На k-м шаге с помощью одномерного поиска в направлении , находим минимум . Это определяет точку .
Шаг 3. Вычисляются и .
Шаг 4. Направление определяется из соотношения
(4.4)
После (n+1) итерации (k=n) процедура циклически повторяется с заменой на .
Шаг 5. Алгоритм заканчивается, когда , где - произвольная константа.
Метод Полака-Рибьера
Метод Полака-Рибьера является разновидностью метода Флетчера-Ривза. Ниже приводятся операции этого алгоритма:
Шаг 1. В вычисляется
.
Шаг 2. На k-м шаге с помощью одномерного поиска в направлении , находим минимум . Это определяет точку .
Шаг 3. Вычисляются и .
Шаг 4. Направление определяется из соотношения
(4.5)
После (n+1) итерации (k=n) процедура циклически повторяется с заменой на .
Шаг 5. Алгоритм заканчивается, когда , где - произвольная константа.
4.2.2 Квазиньютоновские методы (методы переменной метрики)
Методы переменной метрики называют также квазиньютоновскими или градиентными с большим шагом.
В этих методах в процессе поиска осуществляется аппроксимация матрицы вторых частных производных или обратной к ней. Причем для этого используются только первые производные.
Строиться квадратичная модель оптимизируемой функции в окрестностях текущей точки.
, (4.6)
где матрица является аппроксимацией матрицы Гессе.
Квадратичная модель приводит к линейной модели для градиента.
(4.7)
Направление движения из в находят из уравнения:
(4.8)
Общий алгоритм методов оптимизации, использующих аппроксимацию матрицы вторых производных представлен ниже.
Шаг 1. Расчет матрицы .
Шаг 2. Расчет градиента в текущей точке.
Шаг 3. Расчет направления
Шаг 4. Расчет шага.
Шаг 5. Расчет новой точки .
Шаг 6. Пересчет матрицы .
Шаг 7. Проверка критерия останова. Если не выполняется, то положить и перейти на Шаг 2.
Матрица должна обладать двумя свойствами:
- Симметричность.
- Положительная определенность.
(4.9)
Если , , тогда соотношение секущих для оптимизации будет иметь вид
(4.10)
Способы пересчета породили ряд методов, которые называются квазиньютоновские методы.
Метод BFGS
В методе BFGS в качестве выбирается единичная матрица, а пересчет матрицы осуществляется по следующей формуле:
(4.11)
Данная формула гарантирует симметричность и положительную определенность матрицы секущих на каждом шаге итераций.
Метод DFP
В методе DFP в качестве также выбирается единичная матрица, но на каждой итерации сразу производится пересчет матрицы , что избавляет от необходимости обращения матрицы аппроксимации вторых производных. Пересчет матрицы осуществляется по следующей формуле:
(4.12)
4.3. Методы второго порядка
Методы второго порядка при поиске минимума используют информацию о функции и ее производных до второго порядка включительно. К этой группе относят метод Марквардта, метод Ньютона и его модификации.
В основе метода лежит квадратичная аппроксимация функции , которую можно получить, отбрасывая в рядах Тейлора члены третьего и более высокого порядков:
(4.13)
где - матрица Гессе, представляющая собой квадратную матрицу вторых частных производных в точке .
Направление поиска находится из следующего соотношения
, (4.14)
где - остаточный член разложения в ряд Тейлора до второго порядка.
Способы учета матрицы породили различные методы оптимизации второго порядка.
4.3.1. Метод Ньютона
В методе Ньютона остаточный член отбрасывается, и направление вычисляется по формуле
. (4.15)
Необходимым условием вычисления направления по формуле (4.15) является положительная определенность матрицы . Если это условие не выполняется, то направление находится по формуле
. (4.16)
Пересчет следующей точки производится следующим образом:
(4.17)
Алгоритм метода Ньютона состоит из следующих шагов:
Шаг 1. Задать начальную точку , .
Шаг 2. Вычислить градиент в текущей точке .
Шаг 3. Вычислить матрицу Гессе .
Шаг 4. Вычислить матрицу .
Шаг 5. Проверить выполнение условия
а) если , то перейти к шагу 6
б) если нет, то перейти к шагу 7, вычислив как .
Шаг 6. Расчет направления , . Переход на шаг 8.
Шаг 7. Поиск шага из условия минимизации функции
Шаг 8. Расчет новой точки .
Шаг 9. Проверка критерия останова. Если не выполняется, то положить и перейти на Шаг 2. 4.3.2. Метод Ньютона-Рафсона
В методе Ньютона-Рафсона, направление поиска вычисляется, так же как и в методе Ньютона, но шаг вычисляется на каждой итерации, независимо от способа расчета направления из условия минимизации функции .
Алгоритм метода Ньютона-Рафсона состоит из следующих шагов:
Шаг 1. Задать начальную точку , .
Шаг 2. Вычислить градиент в текущей точке .
Шаг 3. Вычислить матрицу Гессе .
Шаг 4. Вычислить матрицу .
Шаг 5. Проверить выполнение условия
а) если , то перейти к шагу 6
б) если нет, то перейти к шагу 7, вычислив как .
Шаг 6. Расчет направления .
Шаг 7. Поиск шага из условия минимизации функции
Шаг 8. Расчет новой точки .
Шаг 9. Проверка критерия останова. Если не выполняется, то положить и перейти на Шаг 2.
4.3.3. Метод МарквардтаЭтот метод является распространенной альтернативой метода Ньютона и его модификаций. Он основан на замене выражением , где
- параметр регуляризации,
- единичная матрица.
Итерационная формула имеет вид:
(4.18)
где - регулирует длину шага и корректирует направление поиска. - это последовательность положительных чисел, таких, что матрица положительна определена на каждой итерации. Как правило, число назначается как минимум на порядок больше, чем самый большой элемент матрицы , а в ряде стандартных программ полагается .
Пересчет осуществляется по следующим правилам: если , то ; в противном случае .
Алгоритм метода Марквардта состоит из следующих шагов:
Шаг 1. Задать начальную точку , , .
Шаг 2. Вычислить градиент в текущей точке .
Шаг 3. Вычислить матрицу Гессе .
Шаг 4. Вычислить матрицу .
Шаг 5. Вычислить матрицу .
Шаг 6. Вычислить
Шаг 7. Расчет новой точки .
Шаг 8. Проверить выполнение условия :
а) если неравенство выполняется, то перейти к шагу 9
б) если нет, то перейти к шагу 10.
Шаг 9.. Переход на шаг 11.
Шаг 10. . Переход на шаг 4.
Шаг 11. Проверка критерия останова. Если не выполняется, то положить и перейти на Шаг 2.
4.4. Методы поиска минимума для функции одной переменной
Для любых методов полиномиальной интерполяции необходимо выбрать такие начальные точки, чтобы оптимум был заключен в интервале ограниченном этими точками. Для этого можно использовать метод Свена или оценивать знак производной.
4.4.1. Квадратичная интерполяция
Если известны значения функции в трех различных точках , , , равные соответственно , , , то функция может быть аппроксимирована квадратичной функцией
(4.19)
где A, B и C определяются из уравнений:
(4.20)
После преобразований этих уравнений получаем
(4.21)
будет иметь минимум в точке , если A>0. Следовательно, можно аппроксимировать точку минимума функции значением
(4.22)
4.4.2. Метод первого приемлемого значения
Метод первого приемлемого значения отличается от квадратичной интерполяции тем, что полином строится исходя из значений в двух точка и и значения производной в одной из этих точек. Тогда значения коэффициентов полинома (4.13) определяются из соотношений
(4.23)
Получаем следующие значения для коэффициентов полинома:
(4.24)
(4.25)
(4.26)
4.4.3. Кубическая интерполяция
Предполагаем, что известны следующие значения:
(4.27)
Эту информацию можно использовать для построения кубического полинома
(4.28)
который будет аппроксимировать функцию . Если , то уравнения, определяющие a, b, c и d выглядят так:
(4.29)
Эти уравнения имеют следующее решение:
(4.30)
В более общем случае (для любых значений и решение системы имеет следующий вид:
(4.31)
Решение уравнения определяет стационарную точку кубического полинома.
4.5. Методы расчета градиента
4.5.1. Численный расчет градиента
Метод численного вычисления градиента основан на использовании определения производной: .
Пусть имеется функция многих переменных , тогда частные производные вычисляются по следующей формуле:
. (4.32)
Значение выбирается в каждом случае индивидуально и зависит от вида функции .
Таким образом, для вычисления значения градиента функции переменных необходимо вычислить значение функции раз.
4.5.2. Расчет градиента с помощью метода быстрого дифференцирования
Пусть - сложная функция многих переменных являющаяся комбинацией функций из множества . Для каждой функции известны выражения для частных производных .
Тогда функцию можно представить в виде ориентированного графа с входными вершинами и одной конечной вершиной. Входным вершинам соответствуют атрибуты , а остальным вершинам соответствуют функции . Пример такого графа для функции
(4.33)
представлен на рис 4.1.
Рис. 4.1. Ориентированный граф для вычисления функции (4.33).
Вычисление значения для каждой вершины графа производится по следующей формуле:
. (4.34)
С каждой вершиной графа, принадлежащей ненулевому слою, ассоциируется автомат, вычисляющий функцию , где - метка вершины. Автоматы срабатывают по слоям в дискретные моменты времени (такты) - автоматы i-го слоя в i-й момент времени. В начальный момент сформированы значения вершин нулевого слоя - известны значения переменных и констант. Они поступают на входы автоматов первого слоя в соответствии с нумерацией аргументов. После i-го такта функционирования определены значения вершин, принадлежащих слоям . На i+1-м такте автоматы i+1-го слоя вычисляют значения вершин i+1-го слоя, получая входные сигналы с предыдущих слоев.
Вычисление градиента сложной функции многих переменных также будет представлено как некоторый вычислительный процесс, в ходе которого сигналы перемещаются в обратном направлении - от выходных элементов графа к входным. И так же, как при вычислении сложной функции, будет явно представлено прохождение каждого узла, а весь процесс в целом будет складываться из таких элементарных фрагментов за счет структуры связей между узлами. Сама эта структура - та же самая, что и для прямого процесса.
Основной инструмент при построении двойственного функционирования - формула для дифференцирования «двухслойной» сложной функции нескольких переменных:
. (4.35)
Для расчета градиента функции , представленной в виде ориентированного графа каждой вершине графа ставится в соответствие двойственная переменная . Для конечной вершины . Для остальных вычисление производится по формуле:
, (4.36)
где - соответствующая вершине функция от независимых переменных и констант, отмечающих вершины нулевого слоя , - соответствующая вершине переменная или константа. Производные в (4.36) берутся при фиксированных значениях прочих переменных и констант. Двойственные переменные вычисляются последовательно, начиная с последнего слоя и заканчивая нулевым. Двойственные переменные вершин слоя являются значениями частных производных функции по соответствующим атрибутам.
Библиографический список
- Д. Химмельблау Прикладное нелинейное программирование. – М.:Мир, 1975. – 534 с.
- Г. Рейклейтис, А. Рейвиндран, К. Рэгсдел Оптимизация в технике: В 2-х книгах. Пер. с англ. - М.:Мир 1986 г. 345 с., 320 с.
- М. Мину Математическое программирование. Теория и алгоритмы. М.:Наука. Гл. ред. физ.-мат. лит., 1990 г. 488 с.
- Б. Банди Методы оптимизации. Вводный курс: Пер. с англ. – М.:Радио и связь, 1988, - 128 с.
- А.В. Пантелеев, Т.А. Летова Методы оптимизации в примерах и задачах. Учебное пособие. М.: Высшая школа, 2002 г., 544 с.
Смотрите также:
Лабораторная работа №3 "Методы оптимизации первого и второго порядков" 242.83kb. 1 стр.
Если в десятичной записи обоих чисел использованы различные цифры и каждая цифра первого числа является делителем второго, а каждая цифра второго числа является делителем первого 43.55kb. 1 стр.
Лабораторная работа 01 Изучение электростатического поля Москва 2005 г. Лабораторная работа №01 64.11kb. 1 стр.
moglobi.ru
Лабораторная работа ’ 11 Оптимизация и настройка Windows XP Цель- получение практических навыков по оптими
Работа добавлена на сайт samzan.ru: 2015-12-26Лабораторная работа № 11
Оптимизация и настройка Windows XP
Цель: получение практических навыков по оптимизации WINDOWS XP.
Теоретические сведения
- Оптимизация WINDOWS
- Удаление лишних папок.
Для уменьшения размера, занимаемого Windows XP, удалить папку %SystemRoot%\Driver Cache\i386\. Отключить режим System Restore, удалив тем самым информацию из папки System Volume Information. Удалить папку %SystemRoot%\system32\dllcache\. По умолчанию размер этой папки - 400 Мб. Он задается в реестре параметром SFCQuota (0xFFFFFFFF), находящимся в ключе HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows NT\CurrentVersion\Winlogon/. С помощью команды sfc: sfc /cachesize=0 его можно сократить до нуля (или до любого другого желаемого значения).
- Настройка BIOS.
Значение параметра Bank 0/1, 2/3, 4/5 DRAM timing, по умолчанию обычно равное 10ns, изменить на 8ns, Normal, Medium, Fast или Turbo - в зависимости от модели материнской платы. 10ns - самый медленный режим, Turbo - самый скоростной. Но помните: чем выше скорость, тем ниже стабильность работы.
- Эффекты.
Некоторые настройки выполняются на вкладке Оформление (Appearance) в свойствах монитора рис 1 а. Параметры, доступ к которым открывается кнопкой Эффекты (Effects), позволяют настроить переходы в меню, тени и шрифт, включая новую технологию улучшения читаемости шрифта - Microsoft ClearType.
Дальнейшая настройка производительности графического интерфейса выполняется в окне Свойства системы рис.1 б (System Properties), на вкладке Дополнительно (Advanced). Нажав кнопку Параметры (Settings) в разделе Производительность (Performance), можно выбрать максимальную производительность, максимальное качество изображения или средние параметры.
Перейдя к вкладке Дополнительно (Advanced) в окне Параметры быстродействия (Performance Options) рис. 2, убедитесь, что распределение ресурсов процессора и памяти ориентировано на оптимизацию работы программ. Если компьютер является сервером, нужно указать приоритет фоновых служб и кэша. Здесь же выбирается размер и местоположение файла подкачки. Но обычно эти параметры Windows XP прекрасно выбирает сама.
- Дефрагментация жесткого диска.
Для ускорения работы системы отключить ненужные системные службы. Заодно и памяти немного освободится. Ниже перечислены службы, которые обычно можно безболезненно отключить.
- Автоматическое обновление (Automatic Updates). Обновлять систему можно и вручную, особенно если нет постоянного соединения с интернетом. Не забудьте только отменить заодно и автоматическое обновление на одноименной вкладке свойств системы.
- Обозреватель сети (Computer Browser). Занимается обновлением списка компьютеров в сети. При отсутствии сети не нужен.
- Служба шифрования (Cryptographic Service). Служба безопасного обмена ключами и шифрования передаваемых данных в локальной сети. Если локальной сети нет, то эту службу можно отключить, если же сеть есть - решайте сами...
- DHCP клиент (DHCP client). Занимается автоматическим распределением IP-адресов. Если сети нет (ни локальной, ни интернета, даже через модем), то эта служба не нужна.
- Журнал событий (Event Log). Ведет журнал системных и программных событий, а также событий системы безопасности. Если вопросы безопасности вас не волнуют, то эту функцию можно отключить.
- Служба сообщений (Messenger). Отвечает за прием и отправку сообщений администратора. При отсутствии сети (и администратора) абсолютно бесполезна.
- Сетевые соединения (Network Connections). Управление всеми сетевыми соединениями. Если сети нет (в том числе и подключения к интернету), то эта служба не нужна.
- Спулер печати (Print Spooler). Не нужен, если нет принтера.
- Portable media serial number. Отвечает за получение серийного номера переносного музыкального устройства, подключаемого к компьютеру.
- Protected Storage. Отвечает за защиту важных данных, в том числе ключей пользователей; запрещает неавторизированный доступ. Если сети нет (в том числе и интернета) или если вас не волнуют вопросы безопасности, то эту службу тоже можно отключить.
- Remote Registry Service. Функция удаленного управления реестром. Нужна только администраторам сети.
- System Event Notification. Отслеживает системные события. Если все уже настроено и нормально работает, можно отключить.
- SSDP Discovery. Обеспечивает работу внешних устройств, поддерживающих UPnP (универсальная система Plug&Play, которая, по задумке, должна связывать компьютер с самой различной бытовой техникой, вроде пылесоса или холодильника).
- Планировщик заданий (Task Scheduler). Обеспечивает запуск приложений в заданное время. Если эта функция не используется, ее можно отключить.
- Telephony. Взаимодействие с модемом. Нет модема - отключаем.
- Telnet. Обеспечивает соединение и удаленную работу по протоколу telnet. Если вы не знаете и не хотите знать, что это такое, эту службу можете отключать.
- Uninterruptible power supply. Управляет работой бесперебойных источников питания (UPS). Если UPS с обратной связью нет, данную службу можно отключить.
- Terminal Service. Служит для удаленного управления компьютером по сети. Домашнему пользователю эта функция, в общем-то, ни к чему.
- Windows time. Синхронизирует время на локальной машине и сервере; если нет time-сервера, то и служба не нужна.
- Wireless zero configuration. Служба автоматической настройки беспроводных сетей стандарта 803.11 и 803.11b.
Отключение Dr.Watson'a - отладчика, запускаемого по умолчанию при каждом сбое в работе приложений. Чтобы отключить этого "доктора", нужно в реестре найти ключ HKEY_LOCAL_MACHINE \SOFTWARE \Microsoft \Windows NT \CurrentVersion \AeDebug и изменить в нем значение параметра Auto на 0.
Изменить значение ключа MenuShowDelay, находящегося по адресу HKEY_CURRENT_USER \ControlPanel \Desktop. В случае установки для этого параметра значения 0 меню будет появляться без задержки.
Изменить ключ MinAnimate, включающий анимацию при сворачивании и разворачивании окон. Он находится по адресу HKEY_CURRENT_USER \ControlPanel \Desktop \WindowsMetrics. Если значение этого параметра 1 - анимация включена, 0 - выключена. Если же этого ключа в реестре нет, создайте его (тип - String).
Удаление скрытых компонентов.
Открыть системную папку %SystemRoot%\Inf, найти в ней файл sysoc.inf и удалить во всех строках слово HIDE. Главное при этом - сохранить формат файла. То есть следует удалять только HIDE, оставляя запятые до и после этого слова. После этого в Add/Remove Windows Components значительно более длинный список, чем тот, что был там прежде.
- Оптимизация с помощью ключей реестра.
В реестре Windows есть несколько ключей, которые позволяют оптимизировать работу Windows с памятью.
- Найдите ключ ClearPageFileAtShutdown в ветви [HKEY_LOCAL_MACHINE \SYSTEM \CurrentControlSet \ControlSessionManager \Memory Management]. Он позволяет удалять файл подкачки при выходе из Windows (этот режим доступен также в разделе локальной безопасности). Его активация приведет к большим задержкам при перезагрузке, поэтому желательно оставить его значение равным 0.
- Ключ DisablePagingExecutive запрещает записывать в файл подкачки коды (драйверы, exe-файлы), всегда оставляя их в физической памяти. Если этой памяти больше 256 Мб, то установка значения в 1 может существенно ускорить работу системы.
- Ключ LargeSystemCache определяет режим работы системного кэша.
- Ключ SecondLevelDataCache предназначен для компьютеров со старыми моделями процессоров (до Pentium II) и позволяет установить размер кэша. По умолчанию его значение равно 0, что соответствует 256 Кб.
Несколько ускорить работу может отключение неиспользуемой подсистемы POSIX. Чтобы не возиться с удалением файлов и с отключением файловой защиты Windows XP откройте [HKEY_LOCAL_MACHINE \SYSTEM \CurrentControlSet \ControlSessionManager \SubSystems] и удалите строки Optional и Posix.
Задания на выполнение лабораторной работы
| № варианта | Задание |
| 1 | Удалить папку %SystemRoot%\Driver Cache\i386\. Отключить режим System Restore. |
| 2 | Удалить папку %SystemRoot%\system32\dllcache\. |
| 3 | В BIOS начение параметра Bank 0/1, 2/3, 4/5 DRAM timing изменить на 8ns. |
| 4 | В BIOS начение параметра Bank 0/1, 2/3, 4/5 DRAM timing изменить на Normal. |
| 5 | В BIOS начение параметра Bank 0/1, 2/3, 4/5 DRAM timing изменить на Medium. |
| 6 | В BIOS начение параметра Bank 0/1, 2/3, 4/5 DRAM timing изменить на Fast. |
| 7 | В BIOS начение параметра Bank 0/1, 2/3, 4/5 DRAM timing изменить на Turbo. |
| 8 | Убрать эффекты рабочего стола. |
| 9 | Произвести дефрагментацию жесткого диска. |
| 10 | Отключить Dr.Watson'a. |
| 11 | Выключить анимацию при сворачивании окна. |
| 12 | Удалить скрытые компоненты. |
| 13 | Запретить записывать в файл подкачки коды (драйверы, exe-файлы), всегда оставляя их в физической памяти. |
| 14 | Отключить Автоматическое обновление (Automatic Updates). |
| 15 | Обозреватель сети (Computer Browser). |
| 16 | Журнал событий (Event Log). |
| 17 | Спулер печати (Print Spooler). |
| 18 | Планировщик заданий (Task Scheduler). |
| 19 | Uninterruptible power supply. |
| 20 | Сократить размер папки %SystemRoot%\system32\dllcache\. |
| 21 | Отключить восстановление системных файлов |
| 22 | Удалить файл подкачки при выходе из Windows. |
| 23 | Отключить графическое ускорение |
| 24 | Изменить меню АВТОЗАГРУЗКА |
| 25 | Реализовать разделение всех настроек для пользователей системы |
| 26 | Включить восстановление системных файлов |
| 27 | Восстанавить файл подкачки при входе в Windows. |
| 28 | В BIOS начение параметра Bank 0/1, 2/3, 4/5 DRAM timing изменить на 1ns. |
| 29 | Включить Автоматическое обновление (Automatic Updates) |
| 30 | Разрешить записывать в файл подкачки коды (драйверы, exe-файлы), всегда оставляя их в физической памяти. |
Контрольные вопросы:
1. Что такое и для чего необходима оптимизиация?
2. Как происходит и для чего необходима дефрагментация дисков?
samzan.ru
Лабораторная работа 7. Исследование методов безусловной оптимизации первого порядка
7.1 Требования задания
Целью работы является изучение методов сопряженных градиентов и методов с переменной метрикой, а также исследование влияния на решение оптимизационной задачи двух способов описания производных - численного и аналитического.
Методы многомерной оптимизации:
М1 - метод Даниела;
М2 - метод Флетчера - Ривса;
М3 - метод Полака - Рибьера;
М4 - метод Дэвидона - Флетчера - Пауэлла;
М5 - метод Бройдена - Флетчера - Шенно;
М6 - метод Бройдена - Флетчера - Гольдфарба - Шенно.
Таблица тестовых функций
| № | Функция y(x) | Начальная точка (x1)t | Значение минимума (x*)t |
| (27) | -12x2+ 4x12+ 4x22- 4x1x2 | ( 1 ; 0 ) | ( 1 ; 2) |
| (28) | (x1- 2)4+ (x1- 2x2)2 | ( 0 ; 3 ) | ( 2 ; 1) |
| (29) | (x1x2x3- 1)2+ 5[x3(x1+x2) - 2]2+ 2(x1+x2+x3-3)2 | ( -5 ; 4 ; 2 ) | ( 1 ; 1 ; 1) |
| (30) | 4x12+ 3x22- 4x1x22+x1 | ( 0 ; 0 ) | ( -1/8 ; ‑3/80000000) |
| (31) | (x12+x2- 11)2+ (x1+x22- 7)2 | ( 0 ; 0 ) | ( 3 ; 2) |
| (32) | 100(x2-x13)2+ (1 –x1)2 | ( -1.2 ; 1) | ( 1 ; 1) |
| (33) | [1.5-x1(1-x2)]2+ [2.25-x1(1-x22)]2+ [2.625-x1(1-x23)]2 | ( 0 ; 0) | ( 3 ; 0.5) |
| (34) | (x1+ 10x2)2+ 5(x3-x4)2+ (x2- 2x3)4+ 10(x1-x4)4 (матрица Гессе в точке х* сингулярна) | (-3 ;-1;0;1) | ( 0 ; 0 ; 0 ;0 ) |
| (35) | 100(x2 -x12)2 + (1-x1)2 + 90(x4-x32)2 + (1-x3)3 + 10.1[(x2-1)2+(x4-1)2]+19.8(x2-1)(x4-1) (функция имеет несколько локальных минимумов) | (-3;-1;-3;-1) | ( 1 ; 1 ; 1; 1 ) |
Варианты задания
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Метод | М1 | М2 | М3 | М4 | М5 | М6 | М2 | М4 |
| Тестовая функция | (21) (24) | (22) (28) | (26) (33) | (27) (32) | (23) (34) | (21) (28), (34) | (19) (29) | (21) (29) |
7.2 Контрольные вопросы
1. Выполните два шага аналитического решения задачи Вашего варианта задания.
2. Определить характер матрицы Гессе функции y(x) = (x2-x1)2+ (1-x1)2в точке минимумаx* = (1,1)t. Используя матрицу Гессе найти направление, сопряженное кp= (1,0)t.
3. Сравните методы переменной метрики по направлениям поиска.
4. Являются ли направления p1= (0,1)tиp2= (1,0)tлинейно независимыми? Ортогональными? Сопряженными?
5. Дана функция y(x) =x12+x22+x32и точкаxk= (1,2,3)t. Определите точкуxk+1 методом Дэниела.
6. Используя метод сопряженных градиентов, найти точку xk+1для функцииy(x) =x12+ 2x1x2+x22иxk= (1,1,1)t.
7.3 Содержание отчета
1. Цель работы и требования задания.
Краткое описание метода оптимизации на основании материала лекционного курса и описание схемы пошагового выполнения вычислительного алгоритма.
Блок-схема программы с пояснением основных ее частей.
Спецификация программы, раскрывающая смысл входных и выходных данных, основных переменных и функций.
Текст программы с детальными комментариями ведущих операторов программы.
Результаты тестирования программы на наборе целевых функций с указанием числа итераций и числа вычислений функций. Таблица, иллюстрирующая вычислительный процесс и изменение ключевых переменных.
Результаты сравнения по числу итераций заданных методов оптимизации при использовании различных критериев окончания поиска, при выборе разных начальных точек x1и при задании различных значений погрешности локализации минимума.
Ответы на контрольные вопросы.
Выводы по работе.
studfiles.net
| Похожие работы | Лабораторная работа № подбор параметра. Оптимизация - страница №1/1 Лабораторная работа № 7. ПОДБОР ПАРАМЕТРА. ОПТИМИЗАЦИЯ1.Подбор параметраПусть имеется некоторая функция одного аргумента, которую обозначим f(x). Предположим, что значение аргумента x мы можем назначать по своему усмотрению. Задача состоит в том, чтобы установить такое значение аргумента x, при котором функция f(x) примет заданное значение c. Мы пришли к известной математической задаче решения функционального уравнения f(x) = с. Пусть f(x) = sin(x) – cos(2x), c = 0, и нам нужно найти корень уравнения на заданном отрезке [0; 2].1.1.Выполнение задания
1.2.Вопросы для контроля
2.ОптимизацияВ состав приложения Microsoft Excel входит мощный инструмент – Решатель (Solver). С его помощью можно решать задачи нелинейного программирования. В частных случаях с помощью Решателя может быть получено решение функционального уравнения, системы линейных уравнений, найден максимум или минимум функции нескольких переменных.2.1.Математическая формулировкаЗадачи, которые могут быть решены с помощью Решателя, в общей постановке формулируются так.Найти значения переменных x1, x2, …, xn, такие, что целевая функция f(x1, x2, …, xn) примет заданное значение, или минимальное значение, или максимальное значение. При этом могут быть заданы ограничения вида g(x1, x2, …, xn), принимающие заданные значения, или значения меньшие или равные заданным, или значения большие или равные заданным. Искомые переменные – ячейки рабочего листа Microsoft Excel называются регулируемыми ячейками. На регулируемые ячейки можно наложить дополнительные ограничения, например, можно потребовать, чтобы значения были положительными или целочисленными. 2.2.Выполнение заданияПродемонстрируем использование Решателя на примере, описанном в журнале «Компьютер Пресс» (№ 7, 1997) в статье В. Очкова «Как я продавал программу (компьютерный этюд)», в которой автор рассказал о применении Решателя для оптимизации своего заработка. Суть задачи состоит в том, что автор продал некоторую программу лакокрасочному предприятию за 14 млн. руб. Наличными деньгами предприятие не располагало, но было готово расплатиться в пределах этой суммы своей продукцией – краской. Краска выпускалась в двух видах тары – больших и малых банках (барабанах), ёмкость которых соответственно составляла 55 и 15 л, а стоимость пустых барабанов – 30 и 24 тыс. руб. Литр краски стоил 14600 руб. Автор статьи был заинтересован в том, чтобы, не выходя за пределы договорной суммы, получить от предприятия как можно больше краски. При этом имеется возможность лишь указать количество больших и малых барабанов с краской, но нельзя взять краску в разлив. Это типичная оптимизационная задача.
2.3.Вопросы для контроля
|
shikardos.ru
Лабораторная работа № 6 Оптимизация нелинейных систем (краткие теоретические сведения)
5
Исследование САУ с помощью среды Matlab © К. Поляков, 2004-2005Лабораторная работа № 6
Оптимизация нелинейных систем
(краткие теоретические сведения)
Эффект насыщения
В реальных системах всегда есть ограничения на максимальную величину управляющего воздействия. В судовых системах управления это, например, предельная скорость электромотора привода, предельное значение угла перекладки руля, предельная скорость перекладки. На малых углах поворота влиянием таких нелинейных ограничений можно пренебречь, однако при больших величинах сигналов они существенно изменяют свойства системы.
Нелинейности такого типа называются «насыщением»:

Они описываются уравнением
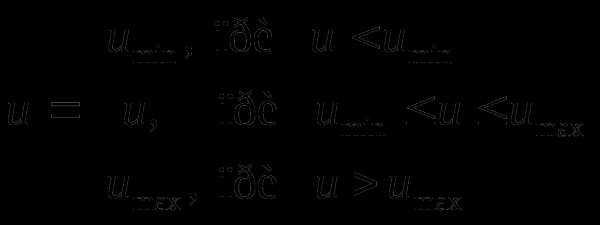 ,
,
где – сигнал на входе звена, – сигнал на выходе (с учетом насыщения), 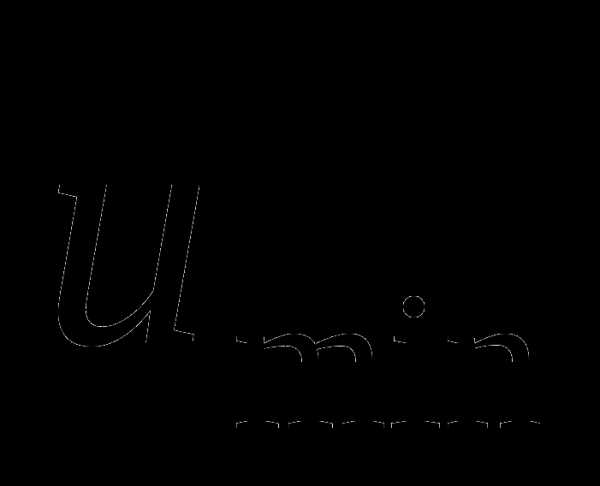 и
и  – допустимые пределы.
– допустимые пределы.
Для компенсации постоянных возмущений в регулятор часто вводится интегрирующее звено. При этом в системах с насыщением наблюдается эффект «залипания» интегратора. Он заключается в том, что управляющий сигнал уже достиг предельного значения, а интегратор продолжает интегрировать («наматывать», windup) ошибку, хотя увеличивать управление уже нельзя. Когда ошибка изменит знак, потребуется переложить руль в другую сторону, но этого не произойдет, поскольку выход интегратора очень велик. В результате увеличивается перерегулирование и время переходного процесса. На практике такое поведение системы может оказаться недопустимым.
Компенсация эффекта насыщения (anti-windup)
Для того, чтобы предотвратить «наматывание» интегратора, используются специальные приемы нелинейной коррекции. Они сводятся к одному из двух вариантов:
Условное интегрирование: если сигнал управления достигает предельного значения, интегратор отключается и интегрирование останавливается
Техникаanti-windup: из входа интегратора вычитается сигнал, который поступает с блока компенсации насыщения. Именно этот вариант мы будем исследовать.
Пусть интегратор включается параллельно остальной части регулятора, т.е., имеет вид
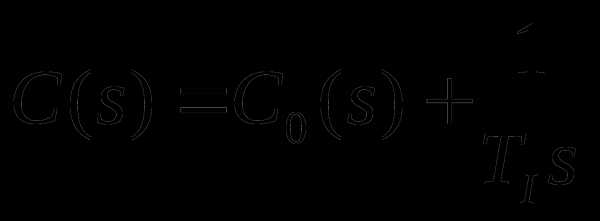 ,
,
где – часть регулятора, не содержащая интегрирующих звеньев, а  – постоянная времени интегрирующего звена.
– постоянная времени интегрирующего звена.
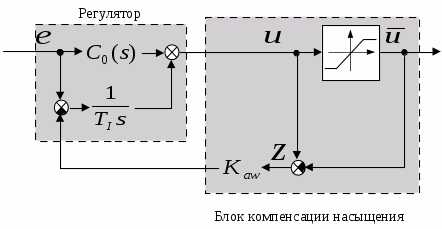
Блок компенсации насыщения генерирует сигнал
,
где – сигнал на выходе регулятора, а – сигнал с учетом насыщения:
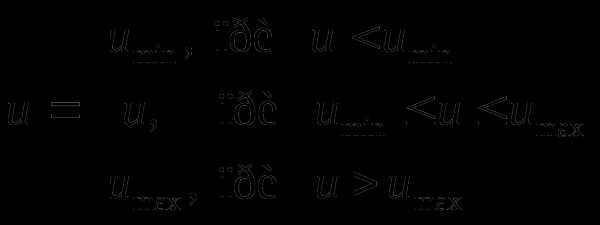 ,
,
причем пределы  и
и 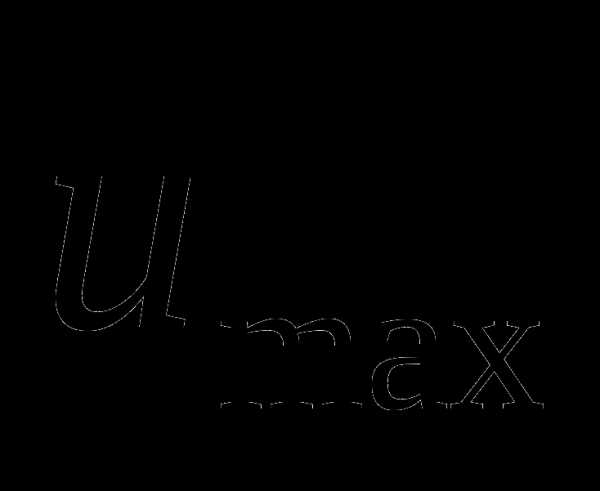 выбираются такие же, как и допустимые пределы для выходного сигнала привода. Если сигнал находится в допустимых пределах (в интервале ), то
выбираются такие же, как и допустимые пределы для выходного сигнала привода. Если сигнал находится в допустимых пределах (в интервале ), то 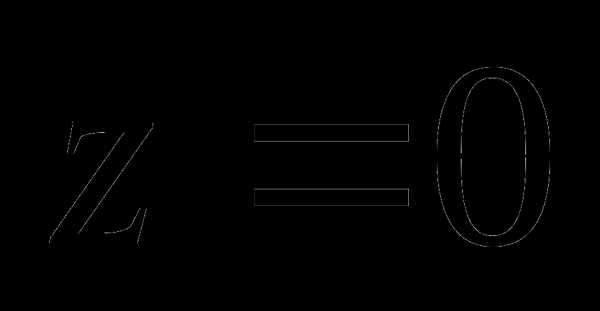 и система работает в линейном режиме, без насыщения. Если же сигнал выходит из диапазона , сигнал
и система работает в линейном режиме, без насыщения. Если же сигнал выходит из диапазона , сигнал 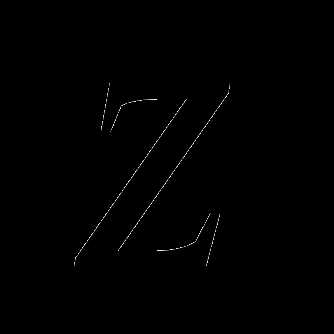 , не равный нулю, подается через усилитель на вход интегратора с обратным знаком, противодействуя «накручиванию» интегратора и возрастанию его выходного сигнала.
, не равный нулю, подается через усилитель на вход интегратора с обратным знаком, противодействуя «накручиванию» интегратора и возрастанию его выходного сигнала.
Заметим, что вместо усилителя с коэффициентом можно устанавливать динамическое звено, однако простейшего варианта часто бывает достаточно.
Аналогичная идея может быть использована и в том случае, когда интегратор подключается последовательно, т.е.,
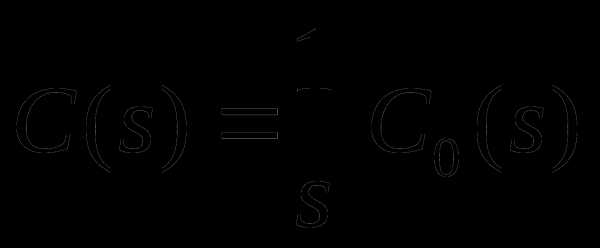 ,
,
где – часть регулятора, не содержащая интегрирующих звеньев. Соответствующая блок-схема системы показана на рисунке.
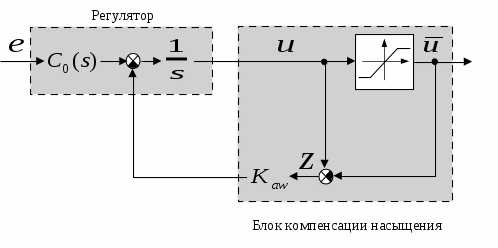
Для того, чтобы выбрать коэффициент , можно использовать различные методы теории нелинейных систем или математическое моделирование. С инженерной точки зрения проще второй способ, который позволяет в интерактивном режиме методом проб и ошибок выбрать подходящее значение . В среде Matlab поиск можно автоматизировать с помощью пакета NCDBlockset (NonlinearControlDesign).
Пакет NCDBlockset
Пакет NCDBlockset (NonlinearControlDesign) предназначен для настройки параметров нелинейной модели методом численной оптимизации по переходному процессу.
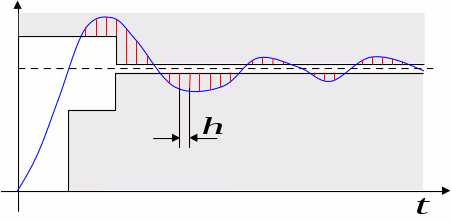
С помощью ломаных линий задается область, из которой не должен выходить переходный процесс. Интервал, на котором выполняется моделирование, разбивается на небольшие участки шириной  . Для этих точек строится система неравенств, которым должна удовлетворять функция, описывающая переходный процесс. На рисунке отрезками красного цвета показано, где эти неравенства нарушены. Требуется выбрать параметры модели так, чтобы нарушений было как можно меньше и величины отклонений были минимальны. В идеале весь переходный процесс вписывается в допустимую область, нарушений вообще нет.
. Для этих точек строится система неравенств, которым должна удовлетворять функция, описывающая переходный процесс. На рисунке отрезками красного цвета показано, где эти неравенства нарушены. Требуется выбрать параметры модели так, чтобы нарушений было как можно меньше и величины отклонений были минимальны. В идеале весь переходный процесс вписывается в допустимую область, нарушений вообще нет.
Для решения этой задачи в пакете NCDBlockset используются процедуры нелинейной оптимизации с ограничениями из пакета OptimizationToolbox.
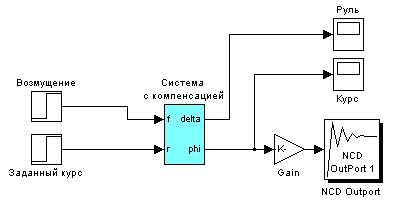
Сначала надо перетащить в модель Simulinkблок NCDOutport из группы NCDBlockset и подать на его вход сигнал, который надо «вписать» в заданную область. По умолчанию границы области устанавливаются так, чтобы установившееся значение сигнала было равно единице. Если это не так, на входе блока NCDOutport можно поставить дополнительный усилитель (блок Gain), который изменит масштаб. Например, если установившееся значение равно 10, коэффициент усиления надо сделать равным 0.1, чтобы установившееся значение на входе блока NCDOutport было равно 1.
Двойной щелчок по блоку NCDOutport открывает рабочее окно для подбора параметра.
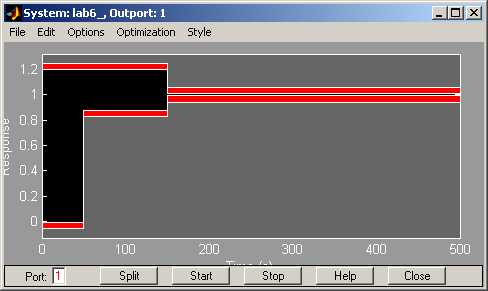
Перетаскивая красные полоски вверх и вниз, можно менять границы допустимой области (она залита черным цветом). Можно также перетаскивать влево и вправо вертикальные границы. Щелчок ПКМ по красной полосе позволяет задать параметры ограничения более точно в диалоговом окне.
Для того, чтобы разбить полоску на две (сделать более точную границу) надо выделить ее щелчком мыши и щелкнуть по кнопке Split.
Чтобы задать параметры поиска, надо выбрать в этом окне пункт верхнего меню Optimization – Optimization Parameters:
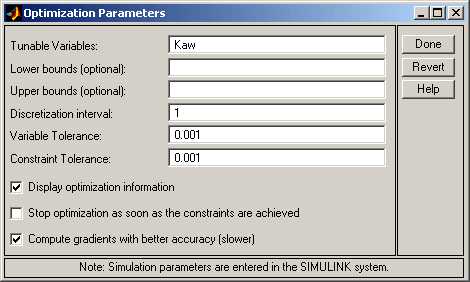
В поле Tunablevariables вводятся через пробел имена переменных, значения которых требуется подобрать. Поля Lowerbounds (нижние границы значений переменных) и Upperbounds(верхние границы) необязательны для заполнения.
В поле Discretizationinterval надо ввести величину шага h (см. рисунок выше). От шага зависит количество интервалов и количество ограничений. Чем меньше шаг, тем больше задается ограничений и медленнее работает процедура поиска. С другой стороны, при очень большом шаге снижается точность. Рекомендуется выбирать этот параметр равным 1-2% от общего времени моделирования.
Перед запуском процедуры оптимизации надо ввести первое приближение для неизвестных параметров в командном окне Matlab:
Kaw = 0.2;
После этого следует щелкнуть по кнопке Start в окне блока NCDOutport. Информацию о ходе процесса и сообщения об ошибках можно наблюдать в командном окне Matlab. Обычно для того, чтобы добиться качественных переходных процессов, приходится несколько раз запускать процедуру оптимизации, меняя ограничения и последовательно улучшая результат.
textarchive.ru
Лабораторная работа - Оптимизация работы предприятия
Лабораторная работа - Оптимизация работы предприятияДоступные файлы (1):n1.doc
Министерство образования и науки Российской ФедерацииФедеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
"Уфимский Государственный Нефтяной Технический Университет"
Кафедра «Математические методы в экономике»
Лабораторная работа №5:
«Оптимизация работы предприятия»
по курсу: « Экономико – математическое моделирование»
(вариант 9)
Проверил: доцент кафедры ММ,
к.т.н. Сулейманов И.Н.
Уфа 2009
Введение
В общем виде задача оптимального планирования выпуска продукции на промышленном предприятии ставится следующим образом. Предприятие может выпускать видов продукции . В производственном процессе участвуют видов ресурсов (сырье, материалы, различные группы оборудования). По каждому - ому ресурсу известен имеющийся его объем , а также известны прогрессивные нормы затрат . На единицу - ого вида продукции. Известна также цена или прибыль на единицу каждого вида продукции. Требуется составить оптимальный план выпуска продукции с учетом ограниченных ресурсов.
Математически данную задачу можно сформулировать следующим образом:
при условии
максимизировать .
В качестве критерия оптимальности варианта делового бизнес – плана примем максимум объема продукция в стоимостном выражении ( - цена единицы продукции) или максимум прибыли ( - прибыль от реализации единицы продукции).
Кроме этих двух критериев оптимальности, могут быть приняты, например, такие, как: минимизация издержек производства, максимизация использования производственных ресурсов и другие. В том случае, если предприятию задается заказ по выпуску некоторых видов продукции, в модель вводится дополнительная система ограничений:
, где - государственный заказ по выпуску продукция вида .
1. Задача:
Цех может выпускать пять видов продукции П1, П2, П3, П4, П5 без ограничения на количественный выпуск этой продукции. Для изготовления этой продукции цех располагает в течении смены следующими ресурсами:
- трудовыми ресурсами в количестве 24 человеко - часов
- полуфабрикатами массой 12 кг
- станочным оборудованием в объеме 3 станко – часов.
| Продукция /Ресурс | П1 | П2 | П3 | П4 | П5 |
| Трудовые ресурсы (чел./ч) | 1 | 2 | 4 | 8 | 6 |
| Полуфабрикаты (кг) | 3 | 6 | 1 | 10 | 4 |
| Станочное оборудование (ст./ч) | 6 | 0 | 3 | 1 | 7 |
| Цена (руб.) | 9 | 10 | 7 | 20 | 15 |
2.Как изменится стоимость выпущенной продукции при увеличении трудовых затрат на 17 чел./час, на 25 чел./час?
3.Войдет ли продукция П1 в план производства при увеличении ее цены на 15 рублей?
2. Ход работы:
Представим исходные данные в матричной форме:
| Вид продукции | Ресурсы | Цена за единицу продукции | ||
| 1 | 2 | 3 | ||
| Продукция 1 | 1 | 3 | 6 | 9 |
| Продукция 2 | 2 | 6 | 0 | 10 |
| Продукция 3 | 4 | 1 | 3 | 22 |
| Продукция 4 | 8 | 10 | 1 | 16 |
| Продукция 5 | 6 | 4 | 7 | 14 |
| Ограничения по ресурсам | 24 | 12 | 3 | |
Полученную модель оптимального производственного планирования решим методами линейного программирования.
| Вид продукции | Ресурсы | Оптимальный выпуск | Цена за единицу продукции | ||
| Трудовые | Полуфабрикаты | Станочное оборудование | |||
| Продукция 1 | 1 | 3 | 6 | 0 | 9 |
| Продукция 2 | 2 | 6 | 0 | 0 | 10 |
| Продукция 3 | 4 | 1 | 3 | 0,62 | 7 |
| Продукция 4 | 8 | 10 | 1 | 1,14 | 20 |
| Продукция 5 | 6 | 4 | 7 | 0 | 15 |
| Итого | 11,59 | 12,00 | 3,00 | ||
| Ограничения по ресурсам | 24 | 12 | 3 | Доход: | 27,10 |
Проверим, как изменится стоимость выпущенной продукции при увеличении трудовых затрат на 17 чел./час, на 25 чел./час:
| Вид продукции | Ресурсы | Оптимальный выпуск | Цена за единицу продукции | ||
| Трудовые | Полуфабрикаты | Станочное оборудование | |||
| Продукция 1 | 1 | 3 | 6 | 0 | 9 |
| Продукция 2 | 2 | 6 | 0 | 0 | 10 |
| Продукция 3 | 4 | 1 | 3 | 0,62 | 7 |
| Продукция 4 | 8 | 10 | 1 | 1,14 | 20 |
| Продукция 5 | 6 | 4 | 7 | 0 | 15 |
| Итого | 11,59 | 12,00 | 3,00 | ||
| Ограничения по ресурсам | 41 | 12 | 3 | Доход: | 27,10 |
| Вид продукции | Ресурсы | Оптимальный выпуск | Цена за единицу продукции | ||
| Трудовые | Полуфабрикаты | Станочное оборудование | |||
| Продукция 1 | 1 | 3 | 6 | 0 | 9 |
| Продукция 2 | 2 | 6 | 0 | 0 | 10 |
| Продукция 3 | 4 | 1 | 3 | 0,62 | 7 |
| Продукция 4 | 8 | 10 | 1 | 1,14 | 20 |
| Продукция 5 | 6 | 4 | 7 | 0 | 15 |
| Итого | 11,59 | 12,00 | 3,00 | ||
| Ограничения по ресурсам | 49 | 12 | 3 | Доход: | 27,10 |
В обоих случаях при увеличении трудовых ресурсов, оптимальный план не меняется, следовательно, стоимость выпущенной продукции останется прежней.
При увеличении стоимости единицы продукции 1 на 15 ден.ед. ее следует будет включить в план выпуска, так как значение прибыли при этом увеличится.
| Вид продукции | Ресурсы | Оптимальный выпуск | Цена за единицу продукции | ||
| Трудовые | Полуфабрикаты | Станочное оборудование | |||
| Продукция 1 | 1 | 3 | 6 | 0,5 | 26 |
| Продукция 2 | 2 | 6 | 0 | 1,75 | 10 |
| Продукция 3 | 4 | 1 | 3 | 0,00 | 7 |
| Продукция 4 | 8 | 10 | 1 | 0,00 | 20 |
| Продукция 5 | 6 | 4 | 7 | 0 | 15 |
| Итого | 4,00 | 12,00 | 3,00 | ||
| Ограничения по ресурсам | 24 | 12 | 3 | Доход: | 30,50 |
perviydoc.ru