Методы на основе пошаговой одномерной оптимизации. Методы оптимизации одномерной

Методы одномерной оптимизации

Методические указания и задания

к выполнению контрольных работ по дисциплине

«Методы оптимизации»

В своей жизни человек часто сталкивается с ситуацией, когда ему из некоторой совокупности возможных вариантов своего поведения или принятия решения в какой-либо области деятельности необходимо выбрать один. Выбор осуществляется путем сравнения различных вариантов при помощи некоторой количественной их оценки. В этом случае говорят о необходимости решения задачи оптимизации. Оптимизация (от латинского слова «optimus» – наилучший) – поиск наилучшего варианта, при наличии множества альтернативных. По содержанию задачи оптимизации весьма разнообразны. Они могут быть связаны с проектированием технических устройств и технологических процессов, с распределением ограниченных ресурсов и планированием работы предприятий, наконец, с решением проблем, возникающих в повседневной жизни человека. Всевозможные устройства, процессы и ситуации, применительно к которым предстоит решать задачу оптимизации, называют объектом оптимизации.

Постановка задачи оптимизации

Имеется задача, для ее решения нужно формализовать объект и представить его в виде математической модели. Математическая модель – модель, которая определена с помощью математических формализмов. Математическая модель не является точной, а является идеализацией.

Для применения теории оптимизации к решению конкретных задачи нужно выполнить определённую последовательность действий, которая называется постановкой задачи оптимизации. Она включает этапы.

Этап I. Установление границ подлежащей оптимизации системы. Система – некая изолированная часть внешнего мира. Границы системы задают пределы, отделяющие её от внешнего мира. При этом предполагается, что взаимосвязи с внешним миром зафиксированы. Первоначальный выбор границ системы может оказаться слишком жёстким. Для получения адекватного решения нужно включить в систему дополнительные подсистемы, однако это ведёт к увеличению размерности задачи. Следует стремиться к представлению системы в виде изолированных подсистем, которые можно рассматривать независимо от других.

Этап II. Выбор количественного критерия, позволяющего выявить наилучший вариант, называемого характеристическим критерием. Критерии могут быть, в зависимости от конкретной задачи, экономического или технологического характера (минимальная стоимость, максимальный крутящий момент). Независимо от того, какой критерий принят в качестве характеристического, он должен принимать максимальное (или минимальное) значение для наилучшего варианта. Критериев может быть много, тогда задача становится многокритериальной. Существуют методы решения многокритериальных задач, но можно привести многокритериальную задачу к однокритериальной. Для этого один из критериев выбирается в качестве первичного, а остальные становятся вторичными. Первичный критерий используется как характеристический, а вторичные формируют ограничения задачи.

Этап III: определение внутрисистемных переменных, через которые выражается характеристический критерий. Выбор переменных осуществляется с учётом следующих рекомендаций. Нужно разделить переменные, которые меняются в широком диапазоне и переменные, которые фиксированы или меняются слабо. Первые определяются, как независимые переменные, а вторые – как параметры задачи. Параметры задачи разделяют на фиксированные и те, которые испытывают флуктуации под воздействием вешней среды.

Нужно выбрать только те переменные, которые оказывают наибольшее влияние на характеристический критерий.

Этап IV. Построение модели, которая описывает взаимосвязь внутрисистемных переменных. Модель системы описывает взаимосвязь между переменными и отражает степень влияния этих переменных на характеристический критерий. Модель включает в себя основные уравнения материальных и энергетических балансов; уравнения, описывающие физические процессы в системе; неравенства, определяющие области допустимых значений переменных.

Таким образом, задача в виде, пригодном для решения методом оптимизации состоит в минимизации (максимизации) вещественнозначной функции N-мерного аргумента x, компоненты которого удовлетворяют системе ограничений в виде уравнений или неравенств Такая задача называется задачей условной оптимизации. Если задача не содержит ограничения и рассматривается на всем пространстве, то это задача безусловной оптимизации.

Задачи оптимизации классифицируются в соответствии с видом функций , и размерностью векторах.

Задачи без ограничений с называются задачамиодномерной оптимизации, с – многомерной оптимизации.

Если в задаче функции линейны, то это задача слинейными ограничениями. При этом целевая функция может быть как линейной, так и нелинейной. Задача условной оптимизации, в которой все функции линейны, называетсязадачей линейного программирования. Задачи с нелинейной целевой функцией называются задачами нелинейного программирования. При этом если квадратичная функция, то задачей квадратичного программирования. Еслиотношение линейных функций, то рассматривается задача дробно-линейного программирования.

В соответствии с классификацией задач оптимизации классифицируются и методы оптимизации

studfiles.net

Классификация методов одномерной безусловной оптимизации.

Поиск Лекций

Все численные методы одномерной безусловной оптимизации условно можно сгруппировать следующим образом:

1. Методы исключения интервалов (линейный поиск):

1.1. Метод половинного деления;

1.2. Метод «золотого сечения»;

1.3. Метод Фибоначчи;

2. Метод полиномиальной аппроксимации:

2.1. Метод Пауэлла;

3. Методы с использованием производных:

3.1. Метод секущих;

3.2. Метод качательных.

Первые две группы методов используют только значения функции и не требуют вычисления ее производных и называются методами минимизации нулевого порядка.

Методы исключения интервалов накладывают единственное требование на исследуемую функцию: она должна быть унимодальной. Следовательно, указанные методы можно использовать для анализа как непрерывных, так и разрывных функций, а также в случаях, когда переменные принимают значения из дискретного множества. Логическая структура поиска с помощью методов исключения интервалов основана на простом сравнении значений функции в двух пробных точках. Кроме того, при таком сравнении в расчет принимается только отношение порядка на множестве значений функции и не учитывается величина разности между значениями функции.Большим достоинством этих методов является то, что от целевой функции не требуется дифференцируемости и, более того, она может быть не задана в аналитическом виде. Единственное, на чем основаны алгоритмы методов нулевого порядка, это возможность определения значений f(x) в заданных точках, а также, что исследуемая целевая функция в допустимой облас-ти, по крайней мере, обладает свойством унимодальности.

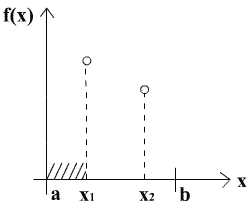
Определение 3. Функция f(x) называется унимодальной, если существует такая точка x*, что из следует , а из следует .

Другими словами, слева от x* функция f(x) монотонно убывает, а справа - монотонно возрастает.

Отметим, что в данном определении не предполагается ни гладкость, ни непрерывность функции.

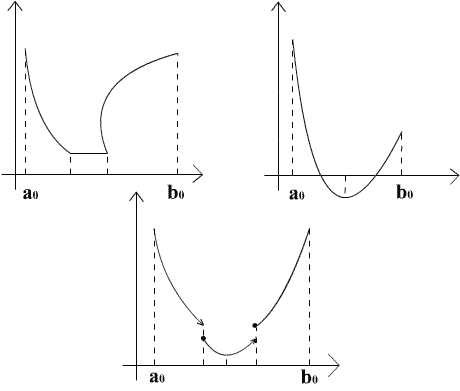
Это важное свойство унимодальных функций. Если мы знаем значения f в точках и отрезка [a,b], , то мы можем определенно сказать на каком из отрезков лежит минимум x* функции f.

Действительно, возможны три различных результата:

a) . В этом случае интервал может быть отброшен.

б) . В этом случае интервал может быть отброшен.

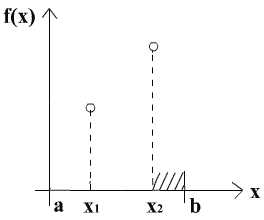
в) . В этом случае интервалы и могут быть отброшены.

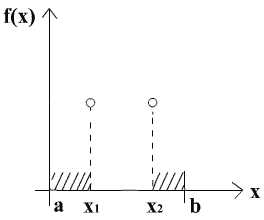
Методы поиска на основе исключения интервалов указывают на отрезок, на котором гарантированно лежит точка x*. Этот отрезок называют отрезком неопределенности. Если в качестве приближенного значения x* взять центр этого отрезка, то погрешность метода есть половина длины отрезка неопределенности.

В отличии от методов исключения интервалов и полимиальной аппроксимации Методы с использованием производных позволяют построить гораздо более быстрые методы, основанные на решении уравнения

Если целевая функция содержит члены, включающие x в третьей и более высоких степенях, то получение аналитического решения уравнения затруднительно. В этих случаях целесообразно использовать численные методы нахождения корней нелинейных уравнений.

Итак, рассмотрим задачу нахождения единственного корня на отрезке [a,b] нелинейного уравнения f(x) = 0 в предположении непрерывности функции f(x).

Геометрически корень x* соответствует точке пересечения графика функции y= f(x) с осью Ох.

Определение 4. . Число x* - есть корень уравнения кратности k, если при x= x * вместе с функцией f(x) обращаются в нуль ее производные до (k-1) порядка включительно, т.е.:

Корень кратности k=1 называется простым.

Так на рисунке корни и – простые, - как минимум кратности 2, как минимум кратности 3.

Если уравнения f(x) = 0 имеет на [a,b] несколько корней, то выполняется операция отделения (локализации) корней, т.е. нахождения достаточно малых окрестностей рассматриваемой области, в которых содержится одно значение корня данного уравнения. Для выявления отрезка, содержащего корень уравнения, следует построить график этой функции.

Для нахождения корней уравнения f(x) = 0 используются различные итерационные методы.

Суть итерационного метода состоит в следующем: генерируется последовательность приближений ,которая сходится к корню в том смысле, что

poisk-ru.ru

Методы одномерной оптимизации — Мегаобучалка

Кафедра компьютерных систем управления и обработки информации

З.Г. Насибов, Н.С. Нестерова, Г.Д. Нестеров

Методы оптимизации

Учебное пособие для студентов специальностей

Программное обеспечение вычислительной техники и

Автоматизированных систем

Вычислительные машины, комплексы, системы и сети

Прикладная информатика (в экономике)

Организация и технология защиты информации

Краснодар

Насибов З.Г., Нестерова Н.С., Нестеров Г.Д.

Методы оптимизации. Учебное пособие для студентов инженерных специальностей по дисциплинам «Методы оптимизации» и «Методы оптимизации и теория принятия решений».

В пособии изложены методы одномерной оптимизации, поисковые методы многомерной оптимизации, методы многомерной оптимизации на основе преобразования задач, рассмотрены некоторые аспекты линейной оптимизации.

Может использоваться при выполнении контрольных и курсовых работ, а также дипломных проектов, связанных с разработкой оптимальных автоматизированных информационных систем.

Учебное пособие рассмотрено и рекомендовано к изданию на заседании кафедры компьютерных систем управления и обработки информации

Протокол 1 от 29 августа 2008г.

Утверждено НМС Академии ИМСИТ

Протокол от 13.10.2008г. № 2

Рецензенты:

Д.т.н., профессор Видовский Л.А.

Д.ф-м.н., профессор Лебедев К.Н.

ВВЕДЕНИЕ

Проблема принятия решения при оптимизации и управлении стала одной из самых острых проблем современности. В любой сфере деятельности человек всегда ищет оптимальные решения. Поэтому совершенно очевидно, что оптимизация, т.е. нахождение способов делать все наилучшим образом, должна интересовать практически представителей любой профессии. Ведь незначительная разница в результатах деятельности человека, функционирования технических объектов или предприятий может привести от процветания к краху.

Процесс оптимизации должен лежать в основе всей инженерной деятельности, поскольку классические функции инженера заключаются в том, чтобы с одной стороны проектировать новые, более эффективные технические системы и с другой – разработать способы повышения качества функционирования существующих систем. Однако в течение длительного времени не существовало возможностей для практического применения методов оптимизации в инженерной практике по следующим причинам:

- недостаток математических знаний у инженеров;

- недостаточная прикладная подготовка методов оптимизации;

- отсутствие вычислительных мощностей.

Сфера применения теории оптимизации в инженерном деле в настоящее время достаточно широка и включает следующие основные направления:

- проектирование систем и их составных частей;

- планирование и анализ функционирования существующих систем;

- анализ и обработка информации;

- управление динамическими системами.

Решение даже несложных задач, в которых число возможных допустимых решений невелико, отыскание оптимального решения, обращающего значения некоторой функции качества в максимум (или минимум), весьма непросто. Используя метод перебора для каждого возможного решения, можно вычислить значение критерия оптимизации и провести сравнение, выбрав требуемое (максимальное или минимальное, в зависимости от задачи) решение. Если число возможных решений велико, то поиск оптимального решения методом перебора фактически невозможен, приходится использовать численные методы теории оптимизации, позволяющие конечным числом шагов найти оптимальное решение.

Как правило, размерность задач оптимизации достаточно велика, что требует выполнения громоздких расчетов и значительных затрат времени. Поэтому оптимизационные методы в основном ориентированы на реализацию с помощью ЭВМ.

В данном учебном пособии приведены некоторые из наиболее употребительных методов оптимизации.

Рассматриваются подробные алгоритмы методов оптимизации, хотя на первый взгляд кажется, что нет особой необходимости в них для пользователей отлаженных программ. Однако только глубокое понимание стратегии поиска оптимума обеспечивает эффективное решение задачи оптимизации в интерактивном режиме.

Такой режим предполагает возможность оперативного взаимодействия исследователя с ЭВМ на любом этапе решения задачи. В частности, в результате диалога «человек – ЭВМ» исследователь может менять число варьируемых переменных, выбирать наилучший метод поиска, подстраивать численные параметры метода к конкретным особенностям оптимизируемой функции, осуществлять адаптацию методов поиска к особенностям и трудностям конкретной задачи и т.д.

Кроме того, глубокое изучение алгоритмов и стратегии поиска оптимума различными методами способствует развитию творческих способностей студента. При таком подходе у студентов могут возникнуть оригинальные идеи по модификации известных алгоритмов оптимизации, значительно расширяющие их возможности.

Методы одномерной оптимизации

Задача оптимизации, в которой критерий оптимальности задан функцией одной переменной, часто встречается в инженерной практике. Кроме того, одномерные методы оптимизации часто используются при решении подзадач многомерной оптимизации. Поэтому анализ задач такого типа занимает центральное место в оптимизационных исследованиях. Это обусловило разработку большого числа методов одномерной оптимизации. Ниже рассматриваются некоторые из этих методов. При этом приводятся алгоритмы поиска максимума целевой функции I(x), где x – параметр оптимизации. Учитывая, что минимуму функции I(x) соответствует максимум функции -I(x), т. е. то изменив знак y минимизируемой функции I(x) на обратный, алгоритмами поиска максимума можно пользоваться и для поиска минимума I(x).

megaobuchalka.ru

Методы на основе пошаговой одномерной оптимизации — КиберПедия

Метод Гаусса-Зейделя (покоординатного спуска)

В основу метода Гаусса- Зейделя положены принципы более раннего метода поочередного изменения переменных. Идея последнего заключается в следующем: из начальной точки делается шаг по первой переменной, если он «удачный», то переходят к следующей переменной. Если шаг оказался «неудачным», то делается шаг в противоположном направлении. Эта процедура повторяется до тех пор, пока во всех направлениях не будут получаться одни «неудачные шаги». В этом случае величина шага уменьшается. Поиск продолжается до тех пор, пока абсолютное значение величины шага оказывается меньше заданной точности.

В методе Гаусса-Зейделя при выполнении шага по каждой переменной ищут минимум целевой функции в ее направлении, при этом значения остальных переменных остаются постоянными. Этот поиск по направлению можно производить любым известным методом одномерной оптимизации (например, методом обратного переменного шага, методом «золотого сечения» и т.п.). Таким образом, в методе Гаусса-Зейделя задача многомерной оптимизации сводится к многократному использованию метода одномерной оптимизации. Очередность варьирования переменных при этом устанавливается произвольно и обычно не меняется в процессе оптимизации [5].

Условием прекращения вычислительной процедуры при достижении заданной точности ε может служить неравенство

При пошаговом движении, например, в алгоритме поочередного изменения переменных поиск прекращается в точке, для которой x(k) совпало с x(k-1), т.е. цикл оказался нерезультативным.

Недостатком метода Гаусса-Зейделя является жесткое направление изменения каждой из составляющих решения, не зависящее от характера функции, что может привести к неоправданной остановке алгоритма в случае «овражных» функций.

Метод Хука и Дживса (метод конфигураций).

Этот метод можно рассматривать как модификацию метода Гаусса-Зейделя. Идея метода заключается в следующем: из начальной (базовой) точки выполняется одна итерация метода Гаусса-Зейделя; там, где получено уточненное значение функции, помещается временная базовая точка. После этого дальнейший поиск проводят вдоль прямой, соединяющий две базовые точки. Этот поиск проводится любым методом одномерного поиска. Найдя точку с минимальным значением целевой функции, из нее снова выполняют одну итерацию метода Гаусса-Зейделя, и дальнейший поиск снова проводят вдоль прямой, соединяющий две последние базовые точки т.д.

Недостатком метода Хука – Дживса, как и метода Гаусса- Зейделя, является его плохая сходимость при оптимизации «овражных» функций, что на стадии исследующего поиска может привести к неоправданной остановке алгоритма.

Симплексные алгоритмы.

Обычный симплекс-метод.

Симплексом в пространстве n переменных называют выпуклый многогранник, имеющий n+1 вершину. В пространстве двух переменных это треугольник, в пространстве трех переменных - тетраэдр. В обычном симплекс- методе используется правильный симплекс (все ребра которого равны). Идея симплекс-метода, заключается в следующем.

Выбирается начальный симплекс с вершинами x(1)-х(2)-х(3). В вершинах исходного симплекса рассчитывается значение целевой функции f(x(1)), f(x(2)), f(x(3)). Из этих трех значений выбирается "наихудшая точка (при поиске минимума это та точка, в которой функция принимает максимальное значение). Допустим, что это точка x(1) . Через центр тяжести противолежащей грани xц.т.=(x(2) + x(3))/2 строится новая вершина симплекса x(4), симметричная "наихудшей" вершине x(1) (рис.4.1):

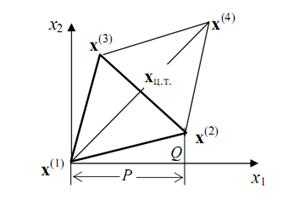
Рисунок 4.1

В результате получается новый симплекс x(2) – x(3) - x(4) , причем значение целевой функции в двух точках x(2) и x(3) уже известно. Поэтому вычисляется значение функции в точке x(4) и среди всех вершин ищется вершина с «наихудшим» значением. Эта вершина вновь отображается через середину противолежащей грани и вся процедура повторяется. Признаком окончания поиска является так называемая процедура зацикливания, когда вновь отображенная вершина оказывается «наихудшей». В этом случае, если заданная точность не достигается (точность обычно определяется длиной ребра симплекса), необходимо уменьшить размеры симплекса. Процедура повторяется до тех пор, пока длина ребра симплекса не станет меньше заданной точности.

В общем n–мерном случае, если обозначить отображаемую вершину симплекса за x(1), остальные вершины – x(2), х(3), …, х(n+1) отображенную вершину за x(n+2), координаты центра тяжести грани, относительно которой производится отображение, определяются по формуле:

а отображаемой вершины

здесь множитель α > 0. При α=1 получаем зеркальное отображение х(1) и если исходный симплекс был правильным, то при зеркальном отображении и новый симплекс окажется правильным.

Метод Нельдера – Мида (деформируемых многогранников).

Данный метод является существенно более эффективным, чем простейший алгоритм регулярных симплексов, за счет того, что симплекс меняет свою форму от цикла к циклу. Рабочий цикл алгоритма состоит из следующих операций [5].

1. Выбирают начальный (обычно регулярный) симплекс x(1) -x(2)-…- x(n+1)

и рассчитывают значения целевой функции в его вершинах.

2. Из найденных значений целевой функции ищут максимальное ymax = f (xmax) и минимальное значение ymin = f (xmin).

3. Отображают «наихудшую» вершину относительно центра тяжести xц.т. противоположной грани с коэффициентом α =1.

4. Анализируют результат отображения, сравнивая значение функции в отображенной вершине с ее значениями в вершинах предыдущего симплекса.

a) Если при этом значение функции в новой вершине оказалось меньше, чем наилучшее значение предыдущего симплекса, т.е. y(n+2) < ymin , то проводят растяжение симплекса, увеличивая в β>1 (обычно β = 2) раз расстояние от отраженной вершины до центра тяжести xц.т.:

(4.1)

Если после операции растяжения значение функции в новой точке уменьшается, т.е. y(n+3) < y(n+2), то эта вершина принимается за вершину нового симплекса. Если же увеличивается, то в качестве новой вершины берется точка, полученная после отображения y(n+2).

b) Когда значение функции в отображенной вершине меньше, чем в наихудшей вершине предыдущего симплекса, но больше, чем во всех остальных, то производят операцию сжатия c коэффициентом β < 1 (обычно β = 0,5) в формуле (4.1).

c) Если значение функции в отображенной точке больше, чем в наихудшей вершине предыдущего симплекса, т.е. y(n+2) > ymax , то производят редукцию (уменьшение размеров симплекса обычно в два раза), т.е. координаты всех вершин симплекса сдвигаются на половину расстояния до наилучшей точки

В качестве критерия остановки используют среднеквадратичную величину разности значений функции в вершинах симплекса и среднего ее значения, т.е.

где ε - заданная точность.

Градиентные методы.

Суть всех градиентных методов заключается в использовании вектора градиента для определения направления движения к оптимуму. Вектор градиента

обладает несколькими свойствами, которые обуславливают его эффективное применение при поиске экстремальных значений функции многих переменных. Выделим некоторые из них.

• Вектор градиента всегда направлен в сторону наиболее быстрого возрастания функции в данной точке. Поэтому очевидно, что при поиске минимальных значений функции необходимо двигаться в противоположную сторону. Такое направление движения называют антиградиентом (-∇f(x)) или отрицательным градиентом и оно характеризует направление наиболее быстрого убывания функции.

• Градиент всегда ортогонален линии равного уровня, проходящей через данную точку x(k).

• Согласно необходимому условию существования экстремума функции многих переменных в точке экстремума градиент функции обращается в ноль. Это свойство часто используется для проверки условия окончания поиска в градиентных методах, т.е.

Общий алгоритм всех градиентных методов заключается в построении из некоторой начальной точки x(0) последовательности приближений (рассматриваем задачу минимизации):

(k=0, 1,…),

где S(k) - единичный вектор в направлении градиента целевой функции f(x)

в точке x(k):

– величина шага в направлении градиента.

cyberpedia.su

Методы одномерной оптимизации

Методы минимизации функций одной переменной, кроме самостоятельного значения, часто являются важным элементом всевозможных методов минимизации функций нескольких переменных.

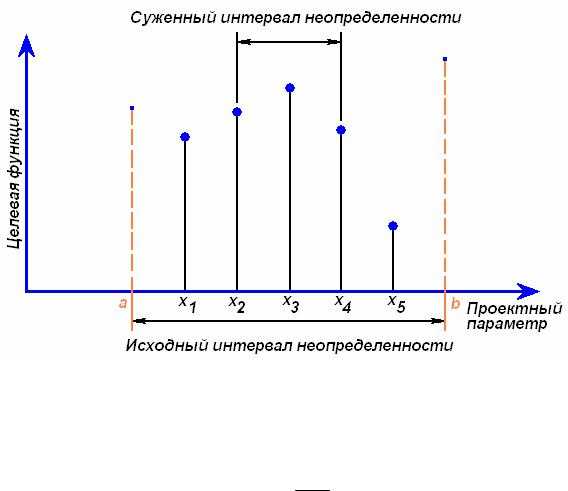
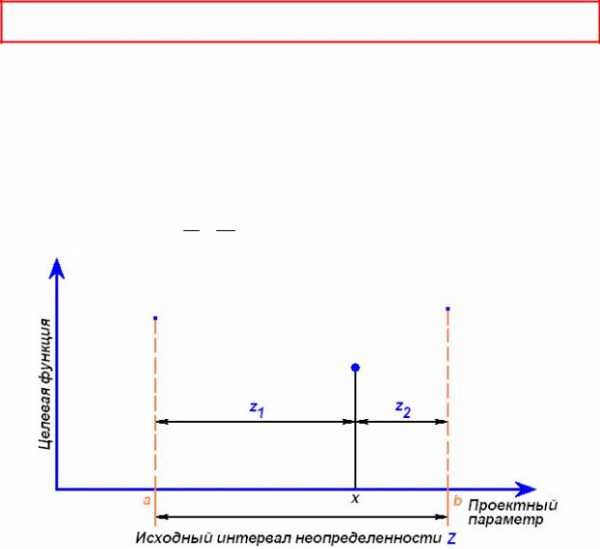
Задачу одномерной оптимизации можно представить следующим образом. Значения единственного проектного параметра х должны быть заключены в интервалеа ≤ x ≤ b. Приступая к решению задачи, мы ничего не знаем о характере изменения целевой функции. Интервал значенийх, в котором заключен оптимум, будем называтьинтервалом неопределенности. В начале процесса оптимизации интервал неопределенности имеет длинуb - а (рис. 5.1).

Существует множество способов систематического сужения интервала неопределенности. Рассмотрим наиболее характерные методы оптимизации и отметим их главные особенности.

5.5.1 Метод общего поиска

Наиболее простым способом сужения интервала неопределенности для одномерной целевой функции является метод общего поиска. При этом интервал неопределенности (рис. 5.8) делится наN равных частей с последующим вычислением значений целевой функции в полученных узлах сетки и выборе из них

минимального (или максимального).

Рисунок 5.8 - Метод общего поиска (ищем максимум)

В результате интервал неопределенности сужается до двух шагов сетки.

Обычно говорят о дроблении интервала неопределенности, которое характеризу-

ется коэффициентом f. Разделив интервал неопределенности наN частей, по-

лучим N+1 узел, и тогда коэффициент дробления для метода общего поискаf =N2+1 .

Чтобы получить значение f = 0.01, потребуется вычислить целевую функцию в199 точках, а приf = 0.001 ужеN = 1999. Несложно заметить, что эффективность метода общего поиска при уменьшении интервала неопределенности стремительно падает.

Можно модифицировать метод общего поиска следующим образом. Чтобы получить коэффициент дробления f = 0.01, вычислим сначала функ-

цию в 19 точках и получимf = 0.1. Затем, вычислив еще19 значений функциина сокращенном интервале неопределенности, получимf = 0.01. Таким образом, по-

требуется всего 38, а не199 вычислений.

Несмотря на очень низкую эффективность, метод общего поиска имеет важное достоинство – используемая целевая функция может быть неунимодаль-

ной и иметь разрывности.

5.5.2 Метод золотого сечения

Наиболее эффективным методом одномерной оптимизации считается ме-

тод Фибоначчи [1]. Лишь немногим ему уступаетметод золотого сечения [1], ко-

торый существенно проще в организации вычислительного процесса и потому нашел большее распространение.

При использовании метода золотого сечения целевая функция обяза-

тельно должна быть унимодальной.

В методе золотого сечения целевая функция вычисляется в точках интервала неопределенности, расположенных таким образом, чтобы каждое вычислен-

ное значение целевой функции давало новую полезную информацию.

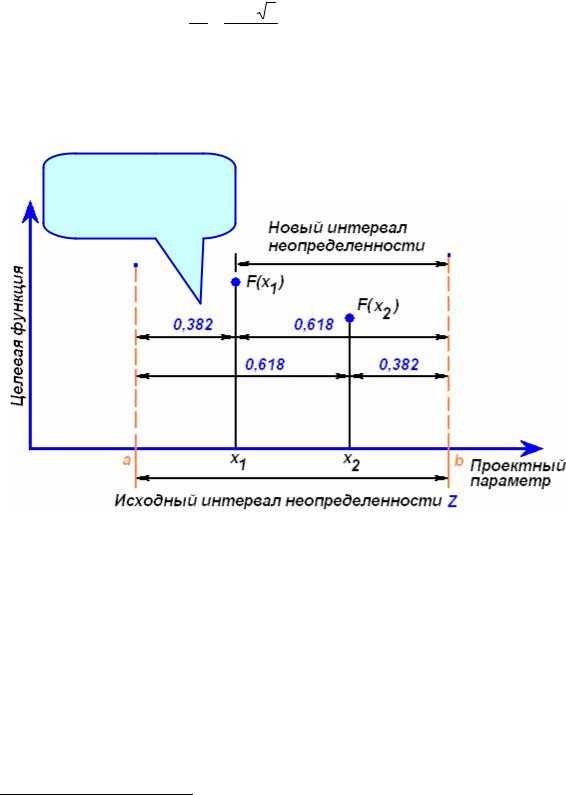
Сущность этого метода состоит в следующем. Интервал неопределенности делится на две неравные части так, что отношение длины большого отрезка к длине всего интервала равно отношению длины меньшего отрезка к длине большего отрезка. На рис. 5.9 показан интервал неопределенностиZ, состоящий из отрезковz1 иz2, отношение длин которых определяется правилом золотого сечения

z1 =z2 , и, кроме того, z1 + z2 = Z.

Z z1

Рисунок 5.9 - Обозначения, используемые в методе золотого сечения

Из первого уравнения следует z12 = Z·z2. Подставляя сюда значениеZ из второго уравнения, и деля затем обе части наz12, получаем

	z2	2		z2
	z2			z2
			+	z −1 =0.
z			+	z −1 =0.
	1			1
Решая это квадратное уравнение, определяем для положительного корня
значение
r = z2	= −1 +			5 = 0.6180339.
z			2
1

На рис. 5.10 изображено деление интервала неопределенности двумя симметрично расположенными точкамиx1 иx2 в «золотом» отношении:

x1 = a+(1 −r()(b−a))≈ a+0.382((b−a))= a+0.382 Z ;. x2 = a+r b−a≈ a+0.618 b−a= a+0.618 Z .

Так как F(x1) > F(x2),

то отбросим интервал a ..x1, перенесяa x1

Рисунок 5.10 - Метод золотого сечения (ищем минимум)

В точках x1 иx2 вычисляются значения целевой функцииF(x1) иF(x2). Сравнение этих значений5 дает возможность отбросить либо интервал[a .. x1], либо интервал[x2 .. b]. Так если нарис. 5.10 мы ищем минимум иF(x1) >F(x2), то следует отбросить интервал[a .. x1]. При каждом таком отбрасывании исходный ин-

тервал неопределенности уменьшается в 1 / 0.618 раза.

На новом интервале неопределенности уже существует одна точка, полученная на предыдущем шаге и осуществляющая его золотое сечение. Таким об-

разом, начиная со второго шага, следует вычислять лишь одно новое значение

целевой функции в недостающей точке нового интервала неопределенности. Положение этой точки определяется правилом золотого сечения по приведенным

выше формулам.

5 Напомним – функцияунимодальная!

studfiles.net

Методы одномерной оптимизации

Поиск Лекций

Методы поиска экстремума функции одной переменной.

Основные понятия.

Несмотря на то, что задача поиска экстремума функции одной переменной наиболее простой тип оптимизационных задач, она занимает центральное место в теории оптимизации, как с теоретической, так и с практической точек зрения. Это связано с тем, что задачи однопараметрической оптимизации достаточно часто встречаются в инженерной практике и, кроме того, находят свое применение при реализации более сложных итеративных процедур многопараметрической оптимизации.

Постановка задачи.

Определение 1. Функция f(x) имеет локальный минимум на элементе , если существует некоторая конечная - окрестность этого элемента, в которой выполняется

Функция может иметь много локальных минимумов.

Определение 2. Функция f(x) достигает глобальный минимум на множестве Х в точке x*, если .

Естественно требовать, чтобы функция f(x) была непрерывной или, по крайней мере, кусочно-непрерывной. В отношении множества Х – это числовая ось.

Если эти требования не соблюдены, то вряд ли можно построить разумный алгоритм нахождения решения. Например, если f(x) не является кусочно-непрерывной функцией, то единственным способом нахождения оптимума является полный перебор всех элементов , на которых задана функция, что вряд ли можно считать приемлемым. Чем более жестким требованиям удовлетворяет f(x) (например, существование производных различного порядка), тем легче построить хорошие численные методы.

Необходимое условие локальной оптимальности.

Необходимое условие локальной оптимальности дается следующей теоремой Ферма.

Теорема Ферма. Пусть f(x) дифференцируема на некотором промежутке и во внутренней точке x* этого промежутка принимает наибольшее (наименьшее) значение, тогда

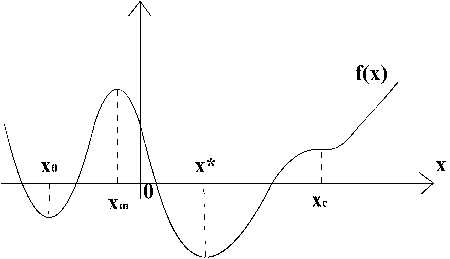
Точки, удовлетворяющие этому условию, называются стационарными (критическими). Стационарные точки могут быть и точками локального минимума, и точками локального максимума, и точками перегиба. Например, на рисунке точка есть точка перегиба. Для определения характера стационарных точек используется достаточное условие локальной оптимальности.

Достаточное условие локальной оптимальности.

Пусть f(x) дифференцируема в точке k раз, k>1, причем Тогда, если k - четное число, то x* - точка локального минимума при и максимума при .Если k - нечетное число, то x* - точка перегиба.

Отметим, что при прохождении точки минимума знак первой производной меняется с «-» на «+», при прохождении точки максимума знак первой производной меняется с «+» на «-», а при прохождении точки перегиба знак первой производной не меняется.

Используя необходимое и достаточное условия оптимальности, находятся точки локальных экстремумов. Для определения абсолютного минимума есть только один способ: найти все локальные минимумы, сравнить их и выбрать наименьшее значения.

poisk-ru.ru

Методы одномерной оптимизации

Метод сканирования основан на табулировании функции в некотором интервале [a,b] значений функции с шагом h:

h = (b-a)/n (28)

где n – количество интервалов разбиения. Последовательно определяются значений функции f(x) во всех точках разбиения аргумента и запоминается наименьшее значение функции Rм и положение минимума (хм) (см. рис. 2).

Рис. 2. Метод сканирования

Если в качестве шага сканирования выбрать заданную точность определения положения минимума e, как это сделано в программе 12, то с этой точностью и получим искомое решение.

В программе 12 реализован метод сканирования одномерной функции R=f(x). Построением графика функции f(x) решается задача отделения одного экстремума. При желании, сканирование можно повторить с новым диапазоном поиска минимума. Эту же программу можно использовать для нахождения максимумов, если в программе сканирования в операторе while x £ b знак £заменить на³. В общем же случае любую программу находящую минимум функции можно превратить в программу поиска максимума, если выражение для функции заключить в скобки и поставить перед ними знак минус.

Программа 12

Метод требует длительных и объемных вычислений для получения минимума с высокой точностью. К достоинствам метода можно отнести тот факт, что алгоритм вычислений очень прост и кроме вычислений функции, практически никаких дополнительных вычислений не требуется. Рекомендуется использовать этот метод для функций, не требующих длительного времени их вычисления. Можно значительно сократить количество обращений к вычислению функции, если использовать методы, описанные ниже. Все они используют итерационные процедуры. На каждом шаге происходит уменьшение первоначального интервала [a,b] поиска.

Эффективность этих методов разная. Коэффициент K эффективности алгоритма тем больше, чем больше степень сжатия интервала поиска на каждом шаге оптимизации и тем меньше количество вычислений функции. Для метода сканирования можно рассчитать:

(29)

где S – количество вычислений функции, за которое начальная длина L диапазона, в котором находится минимум целевой функции, уменьшается до l.

(30)

Очевидно, что для увеличения коэффициента эффективности алгоритма надо увеличить степень сжатия диапазона поиска и уменьшить количество вычислений функции. Рассмотрим для этого алгоритм метода дихотомии, описанный в [10].

Метод дихотомии заключается в следующем. Начальный диапазон поиска делится пополам: х = (a + b)/2 . Затем определяют с какой стороны от х находится минимум. Сравнивают значения функции R(x+e) и R(x-e), где e – некоторая малая величина, выбираемая в начале программы, которая в конце процедуры окажется погрешностью определения минимума. На рис. 3 минимум оказался слева, далее поиск продолжают в диапазоне новых значений a,b,причем b=x, а величина a остается прежней.

Рис. 3. Метод

дихотомии

Таким образом степень сжатия на каждом шаге оптимизации равна 2, при этом число вычислений функции равно 2, следовательно К=1. То есть эффективность метода дихотомии в 2 раза выше, чем сканирования.

Программа 13

Метод золотого сечения. Одним из наиболее эффективных методов по критерию К является метод золотого сечения. “Золотым сечением” или “золотым отношением” называют такое деление отрезка на две части, что “целое к большему относится также, как большее к меньшему”.

Можно показать, что отношение малой части отрезка к целому равно

В методе золотого сечения первоначальный отрезок (a, b) делится на части точками х1 и х2, причем обе точки делят отрезок в золотом соотношении с разных сторон:

Затем сравнивают значения целевой функции R(X1) и R(x2). Если R(X1) > R(x2), то минимум функции, очевидно, находится в интервале (X1, b). Если наоборот, R(X2) > R(x1), то минимум надо искать в диапазоне (a, X2), как это показано на рисунке. На втором шаге новый диапазон поиска также делится в золотом соотношении с двух сторон. И здесь оказывается, что вычислять значение функции R(x2) на втором шаге не надо – оно уже было вычислено как R(X1) на первом шаге. Можно показать, что Z(1-Z)(b-a)=(1-Z-Z)(b-a), если Z – “золотое отношение”.

Степень сжатия интервала поиска в этом методе составляет

Это меньше, чем в методе дихотомии, однако за счет того, что эта степень сжатия достигается не за два, а за одно вычисление функции, коэффициент эффективности в методе золотого сечения больше, чем в полтора раза выше по сравнению с методом дихотомии.

Программа 14

Существует метод одномерной оптимизации, использующий числа Фибоначчи. Этот метод также требует одного вычисления функции на шаге и имеет немного больший коэффициент сжатия, чем в методе золотого сечения. Однако, этот коэффициент не постоянный и при большом числе шагов стремится к 1.618, т. е. эффективность этих методов примерно одинакова.

Для целей отделения экстремумов и нахождения экстремумов очень можно использовать встроенные функции MathCad. После построения графика одномерной функции и отделения экстремумов можно вычислять минимумы и максимумы функции по-отдельности, как это показано в программе 15.

Программа 15

Из листинга программ 12–15 видно, что в пределах заданной точности все методы дают одинаковые результаты.

Контрольные вопросы к главе 4

1. Дайте определение понятию «оптимизация».

2. Как математически формулируется задача оптимизации?

3. Приведите примеры задач оптимизации.

4. Что называют целевой функцией? Приведите примеры.

5. Назовите параметры какой-либо задачи оптимизации в области химии.

6. Как называют оптимизацию с одним параметром?

7. Назовите математические трудности решения задач оптимизации.

8. Чем отличаются условные задачи оптимизации от безусловных?

9. Что обозначает термин «линейное программирование»?

10. Сформулируйте задачу одномерной оптимизации.

11. Чем отличается поиск минимума от поиска максимума?

12. Поясните алгоритм метода сканирования.

13. Какими действиями можно программу поиска минимума одномерной функции методом сканирования превратить в программу поиска максимума той же функции?

14. Как рассчитать коэффициент эффективности алгоритма оптимизации?

15. Поясните алгоритм метода дихотомии.

16. Какие нужны изменения в программе поиска минимума функции методом дихотомии, чтобы с ее помощью можно было найти максимум функции?

17. Каков алгоритм метода поиска минимума одномерной функции методом золотого сечения?

18. Объясните, почему метод золотого сечения более эффективен, чем метод дихотомии?

19. Какие встроенные функции используются в MathCad для решения задач одномерной и многомерной оптимизации?

20. Как можно задать точность вычисления экстремумов в MathCad?

Расчетная многовариантная задача № 4

Найдите 2-3 экстремума функции f(x) с точностью, указанной в таблице методом сканирования, дихотомии, золотого сечения и с помощью встроенных функций MathCad.

Таблица 5

Форма записи отчета в лабораторном журнале:

Дата: ___. Занятие № __. Тема: «Оптимизация». Вариант ___. Получены 3 экстремума с точностью 0.0001:

Граница экстремум [a,b] Положение экстремума

[-1, 0] хmin= - 0.23456

[0, 1.5] хmax = 1.23457

[1.5, 3] хmin = 1.98371

Варианты творческих заданий

1. Проведите аппроксимацию табличных данных Y=f(X) полиномом, причем выбор оптимальной степени полинома проведите одним из методов, описанных в этой главе.

2. Проведите аппроксимацию табличных данных Y=f(X) нелинейной функцией, минимизируя сумму квадратов отклонений (нелинейный МНК) одним из методов, описанных в этой главе. Функцию и табличные данные можно взять у преподавателя.

Дата добавления: 2015-07-19; просмотров: 116 | Нарушение авторских прав

mybiblioteka.su