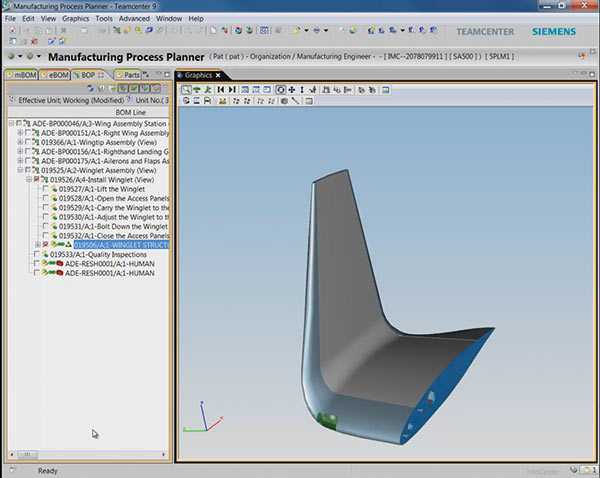
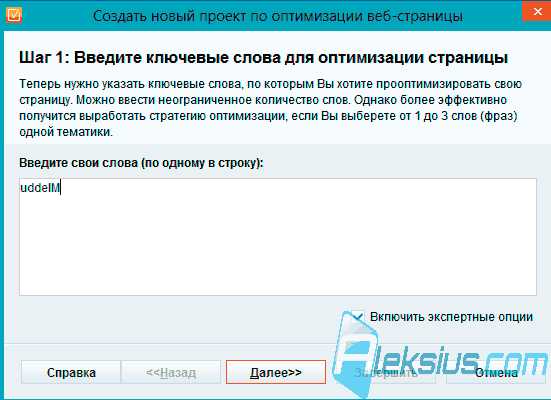
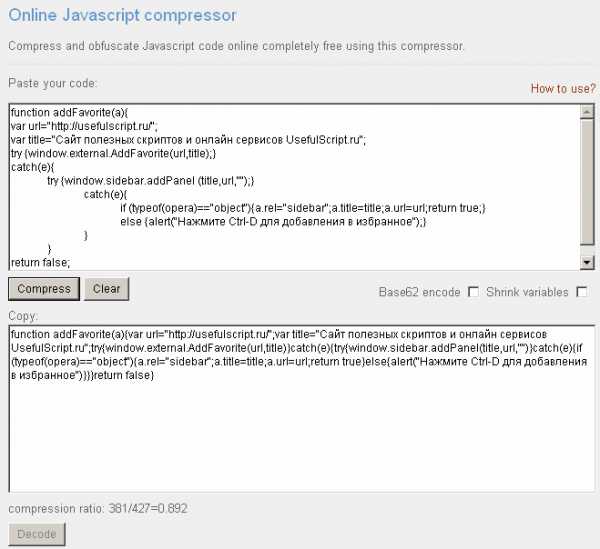
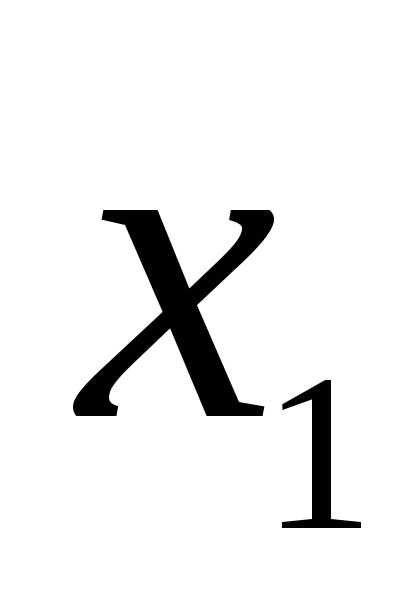Лекции по методам оптимизации - файл n1.doc. Методы оптимизации лекции

Конспект лекций по Методам оптимизации

Конспект лекций по

Методам оптимизации

(для студентов, обучающихся по специальности

071900 “Информационные системы и технологии”)

Составитель: Кривошеев В.П.,

д-р техн.наук, профессор кафедры ИСК

Владивосток

Компьютерный набор

2005 гЛЕКЦИЯ 1Дается определение оптимизации. Отмечаются возможные состояния объекта, задачи оптимизации в зависимости состояния объекта, виды критериев оптимальности и методы решения задач оптимизации.ЛЕКЦИЯ 2Формулируется постановка задачи статической оптимизации. Отмечаются особенности задач статической оптимизации. Указываются методы решения задач статической оптимизации.

Рассматриваются необходимые и достаточные условия экстремума функций одной и нескольких переменных в классическом методе исследования функций на экстремум. Приводятся примеры исследования на экстремум функций одной и нескольких переменных.ЛЕКЦИЯ 3Рассматриваются аналитические методы решения задач статической оптимизации при ограничениях типа равенства (метод множителей Лагранжа) и при ограничениях типа неравенства (условия Куна-Туккера). Приводятся примеры решения задачи указанными методами.ЛЕКЦИЯ 4Излагается сущность методов сканирования с постоянным и переменным шагом, метода половинного деления интервала при численном решении задачи оптимизации для одномерного случая.

ЛЕКЦИЯ 5Излагается сущность методов “золотого” сечения и с использованием чисел Фибоначчи при численном решении задачи оптимизации для одномерного случая. Отмечается область применения методов. Дается сравнительная оценка методов одномерного поиска. ЛЕКЦИЯ 6Приводится способ представления двумерной функции в плоскости переменных. Излагается сущность методов сканирования, Гаусса-Зейделя, градиента и наискорейшего спуска при численном решении задачи оптимизации для многомерного случая. Отмечается область применения и эффективность методов многомерного поиска.ЛЕКЦИЯ 7Рассматривается численный метод решения задач при сильном различии чувствительности целевой функции к переменным (овражный метод).

Излагаются методы численного решения задачи статической оптимизации при условиях типа равенства и типа неравенства методом штрафных функций. Отмечается особенность решения задачи методом штрафных функций.ЛЕКЦИЯ 8Излагается сущность методов случайного поиска. Рассматриваются алгоритмы поиска экстремума функции методом слепого поиска и методом случайных направлений.

Приводится алгоритм движения в выбранном направлении до достижения скорости изменения функции в этом направлении, равной нулю (метод параболической аппроксимации). ЛЕКЦИЯ 9Отмечаются особенности решения задач статической оптимизации большой размерности. Приводятся примеры функций марковского типа и их реализация в многостадийном процессе. Приводятся функциональные уравнения динамического программирования.

ЛЕКЦИЯ 10Рассматривается пошаговый алгоритм решения задачи статической оптимизации методом динамического программирования. Приводятся примеры решения задач статической оптимизации методом динамического программирования.

ЛЕКЦИЯ 11Отмечаются особенности задач оптимизации при линейных целевых функциях и при линейных ограничениях.

Дается понятие базиса, оптимального базиса, форма представления базиса. Приводится пример постановки задачи линейного программирования.

ЛЕКЦИЯ 12Рассматривается алгоритм решения задачи линейного программирования симплекс-методом и его реализация с использованием симплекс-таблиц.ЛЕКЦИЯ 13Формируется постановка задачи динамической оптимизации. Отмечаются особенности задач динамической оптимизации. Указываются методы е решения.ЛЕКЦИЯ 14Излагается сущность классического вариационного исчисления. Приводятся необходимые условия экстремума функционала при наличии связей. Рассматривается алгоритм решения задачи динамической оптимизации методом классического вариационного исчисления.ЛЕКЦИЯ 15Излагается сущность принципа максимума. Рассматривается общий алгоритм решения задачи динамической оптимизации с использованием принципа максимума.ЛЕКЦИЯ 16Отмечается особенность задачи динамической оптимизации для минимизации времени перевода объекта из одного состояния в другое (задача на максимальное быстродействие). Приводится пример решения задачи на максимальное быстродействие.ЛЕКЦИЯ 17Рассматривается применение динамического программирования для решения задачи динамической оптимизации. Приводится уравнение Беллмана и формируются граничные условия для его решения. Отмечается связь классического вариационного исчисления, принципа максимума и динамического программирования в непрерывной форме.

100-bal.ru

Методы оптимизации, 01 лекция (от 08 февраля) — eSyr's wiki

Материал из eSyr's wiki.

[править] Методы оптимизации

МО в хороших университетах для студентов по специальности прикл. математика --- 6 семестров, но у нас полугодовой курс, но это будет предлагать самостоятельную работу, будут давать задачи, их решение висит на сайте, но рекоммендуется рисовать их самостоятельно. В Америке по статистике 70 процентов функционально неграмотны. Это не есть обязательая мера. Для всех, кто хочет сдавать досрочно это обязтельная мера, а также для тех, кто обучается 4 года.

Курс для этого потока непохож на те, которые читаются для 1/2 потоков, там годовой курс, и попросили сделать упор на дискру.

[править] Теория сложности

Лекции 4 будет занимать, основной набор задач по этой теме, эта же тема будет продолжаться в курсе ИО.

[править] Литература

М Гэри, Д. Джонсон. «Вычислительные машины и трудно решаемые задачи», М., Мир, 1982 год

Х. Пападимитриу, К. Сталиц, «Комбинаторная оптимизация», М. Мир, 1985 год

[править] Что такое теория сложности

В чём цель прикладная? Если мы посмотрим, как двигалась научная мысль, то увидим, что сначала люди решали дискретные задачи. Если надо посчитать площадь, длину, то разбивали на кусочки. Но так считать тяжело. Потом Ньютон придумал флюксии, появился анализ… При этом забыли, что дискретные задачи решать сложно.

В конце 60-х годов народ понял, что переборные алгоритмы для существующих задач это сложно. И выяснилось, что да, есть задачи, для которых можно построить алгоритмы, есть задачи, для которых нельзя построить алгоритмы, и возникло направление, которое пыталось доказать по задаче, можно ли найти непереборный алгоритм или нет. На этом и возникла теория сложности, которая хоть эту задачу не решает, но позволяет классифицировать задачи. В книжке Гэри-Жжонсона приводиться более 550 труднорешаемых задач, они все перечисляются по одной, поскольку основной результат теории сложности такой: если удасться найти для одной из этих задач найти непереборный алгоритм или доказать, что такого алгоритма построить нельзя, то это верно и для всех остальных. Задачи разного плана: теория графов, сети, головоломки, оптимизация БД…

[править] Термины

Решить задачу оптимизации — не значит, что нужно решить конкретную задачу, типа «посчитать высоту Униыерситета», это значит написать программу решения определённого класса задач.

Основное понятие — массовая задача (П)

Массовая задача — набор, класс индивидуальных задач (I), П = {I}. Индивидуальная задача получается из массовой путём конкретизации. То есть, у массовой задачи есть свободные параметры.

Задача характеризуется списком параметров (имеются в виду свободные параметры задачи) (конкретные параметры → I)
Требования к решению. Задача поставлена ⇔ поставлены требования к решению.

Классической задачей, модельной задачей, массовой задачей, основной задачей является задача коммивояжёра.

Формулировка: имеется набор городов C = {c1, …, cn}, имеются расстояния между городами, полагаем, что они больше нудя: {dij = d(ci, cj)} > 0 | ci, cj ∈ C}. Коммивояжр должен выйти из города, обойти все, затратив наименьшее расстояние. Другое название — поиск гамильтонова цикла.

Задача имеет воплощение в реальной жизни: вы поступаете не работу, вы или ваши сотрудники ездят по точкам, и вас, как выпускника, просят написать задачу, которая по списку точек выстраивает оптимальный маршрут.

В данном случае C, {dij} — параметры задачи, требования к решению — найти такое &pi: {1, …, m} → {&pi1, …, &pim} ↔ Невозможно разобрать выражение (неизвестная ошибка): \min_{T_{1}} \sum_{j=1}^{m-1} d(c_{\pi(i)}, c_{\pi(i+1)}) + d(c_{\pi(m)}, c_{\pi(1)) .

Другой пример конкретной задачи — организация сети кольцевой архитектуры.

Можно сказать, что зачем нам кольцевая задача (альтернатива — бездомный коммивояжёр), но это столь же сложная задача.

Похожая задача — поиск минимальной связывающей сети, но эта задача уже решаемая.

Если спросить у человека, что проще — построить минимальную связывающую сеть или закольцевать, то немногие ответят, что связать просто, а закольцевать сложно.

Если же теперь на вход подаём какие-то численные значения, то получаем индивидуальную задачу. Можно сказать, чего проще, у нас конечные множества, можно перебрать все варианты. Чтобы рассеить все иллюзии, достаточно сказать, что число вариантов для m городов равно m!. Табличка:

m m!

5	120
8	40320
10	3,6 × 106
13	6,2 × 109
15	1,3 × 1012
30	2,7 × 1032

У телефонной сети была задача обхода автоматов и вытаскивания из них жетонов, совершенно нерешаемая задача. В книге Гэри-Джонса есть замечательная картинка, в которой босс даёт сотруднику задачу, он пытается её решить, придумывает алгоритмы, но они все переборные.

Кроме первичных понятий будем использовать понятие алгоритма (A), понимать под этим формально следующее:

Алгоритм (А) — программа для машины Тьюринга.

Алгоритм А решает массовую задачу П, если для любои индивидуальнй задачи алгоритм применим, т. е. останавливается за конечное число шагов, и даёт решение: A решает П, если &forallI ∈ П А применим и даёт решение I.

Мы будем заниматься массовыми задачами распознавания свойств.

П — задача распознавания свойств, если в качестве требования к решению является ответ «да» или «нет».

Большинство задач без особых качественных изменений записываются в виде задач распознавания свойств, например, для задачи коммивояжёра: мы должны задать число B, которое является критической длиной маршрута, и вопрос выглядит таким образом: «существует ли маршрут длины ≤ B?».

Задачи в этих постановках по сложности эквивалентны, то есть, если будет найде алгоритм для задачи распознавания свойств, то \, не сильно увеличив сложность алгоритма, можно указать алгоритм для исходной задачи.

Также будут применяться следующие обозначения:

D — множество значений параметров задачи
Y — множество значений параметров, для которых соответствующая индивидуальная задача имеет ответ «да»

Этот набор (D, Y) полностью характеризует задачу распознавания свойств. Например, для задачи коммивояжёра:

D = {C = {c1, …, cn}, {dij = d(ci, cj)} > 0 | ci, cj ∈ C}, B}, dij, B ∈ Z+

Если есть алгоритм, который останавливается за конечное число шагов, то для того, чтобы найти сложность алгоритма, нужно связать количество шагов с длиной входного слова. Для того, чтобы формализовать размер задачи, с каждой проблемой П нужно свзяать некую схему кодирования (кодировку) для задания параметров.

Схема кодирования (кодировка): необходимо ввести алфавит Σ — множество, состоящее из конечного числа символов , Σ* — множество слов для алфавита, слово — конечный набор букв, слово будем обозначать &sigma = {σi, σj, σk, …}. Кодировка — e: П → Σ*, ∀I ⇒ e(I) = σ ∈ Σ* — отображение массовой задачи в множество слов, индивидуальная задача отображается в слово.

Можно сказать, что отображение параметров задачи. Отображение должно удовлетворять следующим свойствам:

Возможность декодирования однозначного: ∀I1 ≠ I2, e(I1) ≠ e(I2)
Само кодирование и процесс декодирования должны быть полиминальной сложностиЮ e, e-1 — полиномиальные вычисления
Неизбыточность кодировки: для любой другой кодировки, удовлетворяющей свойствам 1 и 2 найдётся такой полином от n, что для любого натурального n найдётся такая задача I, что длина входа задачи I: — не существует кодировки, которая на порядок лучше

Обычно встречаемся с кодировкой чисел. Какие бывают кодировки: двоичная. Например, есть число N, в двоичной кодировке получаем число N2 = (1, 0, …, 1), |N2| = log2 N, можно взять другую систему: |N10| = log10 N, и в данном случае порядок соответствует.

Другая кодировка: кодирование палочками, длина слова |N1| = N = 2log2 N, и эта кодировка избыточная, так как в этом случае получаем не полином а экспоненту.

Задача 1. Предложить (неизбыточную) кодировку для задачи коммивояжёра и оценить длину входа.

В книге Гэри-Джонсона есть оценка, которая выглядит следующим образом:

Просьба: задачи решать-сдавать, не списывать (лектор готова брать листочки, где указаны максимум 5 человек).

Всем этим задачам (выявления свойств) соответствует Σ*, части их соответствует ответ «да», будем назыать эти слова правильными. Множество правильных слов — язык.

Язык — множество слов, соответствующих правильным решениям: L(Π, e) = у(Н) = {σ ∈ Σ* | Σ — алфавит e, σ = e(I), I ∈ Y}

С любым алгоритмом А, который решают задачу распознавания свойств, связывается язык: A ⇒ L(A) = {σ ∈ Σ* | Σ — алфавит A и A(&sigmal) = qY}

После того, как мы написали алгоритм и написали задачу, мы можем оценить время работы алгоритма.

Время работы алгоритма А, если есму подали на вход слово σ — tA(σ).

Определение 1. A решает задачу П с кодировкой e, если язык алгоритма совпадает с задачей П в кодировке E: L(A) = L(Π, e), и для любого слова из их множества алгоритм останавливается: ∀ σ ∈ Σ* A(σ) останавливается

tA(σ) — число шагов до остановки.

Определение 2. Временна'я сложность алгоритма A решения задчи П — функция TA(.): TA =

Задача 2. Дать алгоритм распознавания простоты числа, оценить временную сложность алгоритма. Что такое задача распознавания простоты числа — есть N, на выходе должны получить «да» — N простое, «нет» — N составное.

[править] Классы сложности задач

Определение 3. Класс полиномиально разрешимых задач = {L(Π, e) | ∃ A решающий Π с кодировкой e, ∃p(.) — полином:

Будем говорить просто: задача принадлежит классу полиномиальных задач: П ∈ P — ежели для неё существует алгоритм с полиномиальной сложностью.

Труднорешаемые задачи — задачи, для которых нет полиномиального алгоритма.

Слово о полиномиальных и экспоненциальных алгоритмах: если есть алгоритм, который имеет полиномиальную сложность, но степено например порядка 7. Это ничем не лучше экспоненты. Но опыт показывает, что через некоторое время появляется алгоритм, который решает задачу с приемлемыми степенями полинома.

Ежели задача не принадлежит классу полиномиальных (П ∉ P), то есть три возможности:

П неразрешима алгоритмически, то есть, нет алгоритма, который не решает любую индивидауальную задачу. Пример: 10-я проблема Гильберта по многочлену с целыми коэфициентами g необходимо найти, имеет ли уравнение g = 0 целочисленные решения. Было доказано (Матюясевич Ю. М.), что эта проблема алгоритмически неразрешима.
Запись решения имеет экспоненциальную сложность
Нет полиномиального алгоритма. Для любой подобной задачи доказано, что не существует полиномиальное решение задачи на МТ, допускающей бесконечный алфавит

Эта статья является конспектом лекции.

Эта статья ещё не вычитана. Пожалуйста, вычитайте её и исправьте ошибки, если они есть.

esyr.org

Методы оптимизации

Лекции по методам оптимизациискачать (606.2 kb.)Доступные файлы (1):

n1.doc

1 2 3 4 5 6 7 8 Методы оптимизации

Построение математической модели

Поиск оптимальных решений

Корректировка

модели

Реальная задача

Выдача рекомендаций

Схема исследования

Математическая модель

Математическая модель — описание решаемой задачи в математических терминах.

Математическая модель описывает исследуемую систему и позволяет выразить ее эффективность в виде целевой функции

W = f(X,Y),

где X = (x1,…, xn) — управляемые переменные,

Y = (y1,…, ym) — неуправляемые переменные (исходные данные).

Связь между переменными X и исходными данными Y выражается с помощью ограничений

 (X, Y)  0.

Виды моделей

детерминированные;
вероятностные;
игровые;
неполные (задачи в условиях неопределенности).

Исследованием детерминированных моделей занимается математическое программирование (МП).Термин «программирование» означает «поиск наилучших планов» (programming – планирование – составление плана или программы действий).

Задача оптимизации

(

)

Задача математического программирования

Оптимальным решением задачи (минимизации) называют допустимое решение, минимизирующее f(x) на множестве всех допустимых решений.

Задачи математического программирования

Транспортная задачаИстория математического программирования

Б.Т. Поляк, Институт проблем управления, Москва История математического программирования в СССР: попытка анализа

История математического программирования

Леонард Эйлер, 1707-1783, первый ученый, занимавшийся оптимизацией в России
Чебышев П.Л., 1821-1894, основы выпуклой оптимизации, решал практические оптимизационные задачи: построение наименее искаженной географической карты, оптимальный раскрой, наилучший выбор параметров механических устройств
А.А. Марков, 1856-1922, известны работы в теории чисел и теории вероятностей (Марковские цепи, Марковские процессы)
А.М. Ляпунов, 1857-1918, разработал теорию устойчивости для дифференциальных обыкновенных уравнений, тем самым внес огромный вклад в развитие непрерывной оптимизации, предложил инструмент для проверки сходимости численных методов оптимизации

История математического программирования5. Л.В. Канторович, 1912-1986, в 1975г. получил Нобелевскую премию в области экономики, один из основателей численного анализа в нашей стране, одним из первых признал информатику как новую ветвь в математике.

Отец новой науки ОПТИМИЗАЦИИ, которая включает стандартное математическое программирование.

С именем Канторовича Л.В.связаны следующие достижения:

Линейное программирование, 1939:

Опубликована книга (67 стр.), в которой рассматривался новый тип оптимизационных задач. Формы записи этих задач были иными, чем стандартная формулировка задачи ЛП, причем модель, рассматриваемая в западной литературе - частный случай модели Канторовича.

Общие условия оптимальности, 1940

Техника функционального анализа, 1939-1948

История математического программирования6. Г.Ш. Рубинштейн, ученик Канторовича Л.В., учитель д.т.н., проф. УГАТУ Мухачевой Э.А.

В 1961г. вышла книга Канторовича Л.В. и Рубинштейна Г.Ш., в которой давались математические формулировки задачи ЛП и приводились численные методы ее решения, были введены понятия двойственных переменных, которые назывались «объектно-обусловленными оценками».

7. В 50-е годы – интенсивные исследования в области ЛП.

Стали известны работы западных ученых: Дж. Данцига, Г.Куна, А. Таккера и др. по ЛП.

Выпущен первый учебник на русском языке по ЛП Юдиным Д.Б., Гольштейном Е.Г.

8. 60-е годы

Появилась общая теория двойственности для задач выпуклой оптимизации (Гольштейн Е.Г.), появились труды по стохастической оптимизации.

История математического программированияВелись разработки ПО для реализации симплекс – метода для решения задачи ЛП (И.В. Романовский, А.А. Станевичус, и др, доцент УГАТУ А.П. Мартынов).

Появились численные методы решения специальных классов задач ЛП:

транспортная задача, методы декомпозиции, итеративные методы ЛП.

Практическое применение ЛП для социалистической экономики.

9. 70-80-е годы

Вводится новое понятие сложности оптимизационной задачи: установлены нижние границы для различных классов оптимизационных задач (Юдин Д.Б. и др.).

Было установлено: если метод имеет сложность, совпадающую с нижней границей, то он оптимален, т.е. не существует методов, которые решают все задачи класса быстрее (в отношении порядка).

Построен итеративный метод решения задачи ЛП, для которой была доказана полиномиальная сходимость (Хачиян Л.Г.) Литература1.Канторович Л.В. Математические методы организации и планирования производства. Л.: Изд-во Ленинградский университет, 1939, 64с.

2. Юдин Д.Б., Гольштейн Е.Г. Задачи и методы линейного программирования. М.: Советское радио. 1964, 491с.

3. Карманов В.Г. Математическое программирование. М.: Наука, 1975, 272с.

4. Мухачева Э.А., Рубинштейн Г.Ш. Математическое программирование. Новосибирск: Изд-во «Наука», Сибирское отделение, 1987, 272с.

5. Мухачева Э.А. Рациональный раскрой промышленных материалов. Применение АСУ. М.: Машиностроение, 1984,174с.

6. Мухачева Э.А., Верхотуров М.А., Мартынов В.В. Модели и методы расчета раскроя-упаковки геометрических объектов. Уфа: УГАТУ, 1998, 217с.

7. Мухачева Э.А., Валеева А.Ф., Картак В.М. Задачи двухмерной упаковки в контейнеры: новые подходы к разработке методов локального поиска оптимума. Москва: Изд-во МАИ, 2004, 192с.

Главные научные центры по математическому программированиюМосква: МГУ, Центральный экономико-математический институт, Вычислительный центрКиев: Институт кибернетики им. В.М. ГлушковаНовосибирск: Институт математики им. С.Л. Соболева Сибирского отделения РАН, Новосибирский государственный университетЛенинград: Ленинградский государственный университет

Задача планирования производства

Вид сырья	Нормы расхода сырья (кг) на одно изделие		Общее количество сырья на складе (кг)
Вид сырья	А	В	Общее количество сырья на складе (кг)
I II III	12 4 13	4 4 12	300 120 252
Прибыль от реализации одного изделия (у.е.)	30	40