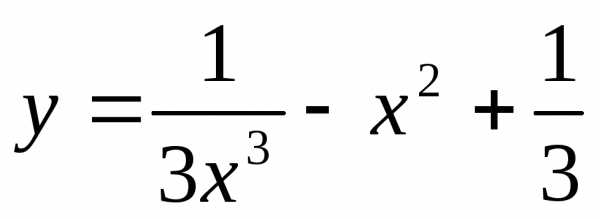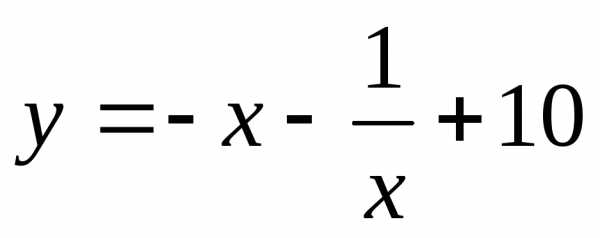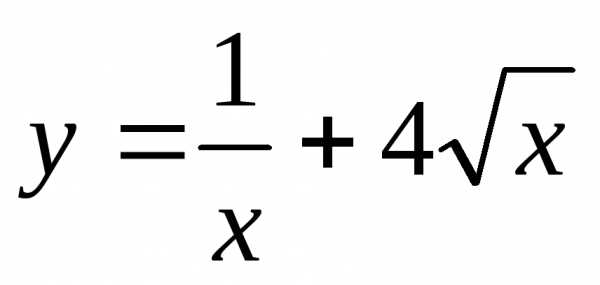Лекция 9: Однопараметрическая (одномерная) оптимизация. Методы одномерной оптимизации: метод дихотомии, метод Фибоначчи, метод "золотого сечения", метод Ньютона. Интервальные методы однопараметрической оптимизации
2. ОДНОМЕРНАЯ ОПТИМИЗАЦИЯ
Оптимизация функции одной переменной – наиболее простой тип оптимизационных задач. Тем не менее, она занимает важное место в теории оптимизации. Это связано с тем, что задачи однопараметрической оптимизации достаточно часто встречаются в инженерной практике и, кроме того, находят свое применение при реализации более сложных итерактивных процедур многопараметрической оптимизации.
Разработано большое количество методов одномерной оптимизации и мы рассмотрим две группы таких методов:
•методы сужения интервала неопределенности;
•методы с использованием производных.
2.1.Методы сужения интервала неопределенности
Пусть требуется найти минимум функции f (x) на некотором интервале [a,b]. Задача приближенного отыскания минимума в методах сужения интервала неопределенности состоит в том, чтобы найти множество абсциссx1,x2 ,...,xk , в которых вычисляется функция, такое, что минимальное значениеf * лежит при некоторомi в интервалеxi−1 ≤ x* ≤ xi . Такой интервал называется интервалом не-
определенности D. Очевидно, что сначала интервал неопределенностиD совпадает с отрезком [a, b].
Существуют несколько способов систематического сужения интервала неопределенности. Рассмотрим три из них.
2.1.1. Общий поиск
Пусть требуется найти минимум функции f (x) на некотором интервале [a,b]. Если о функцииf (x) на этом интервале никакой дополнительной инфор-
мации неизвестно, то для поиска минимума на [a,b] можно применить простейший метод перебора, или, иначе, общего поиска.
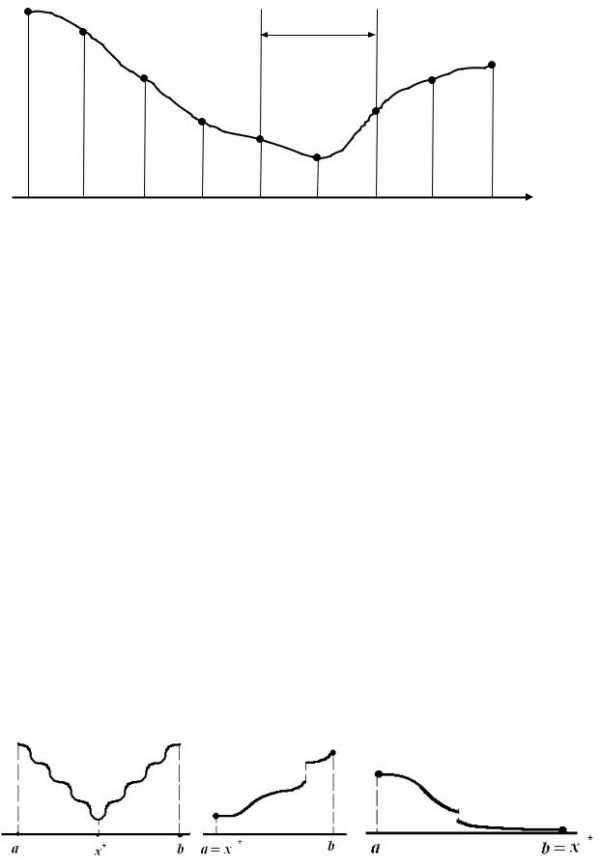
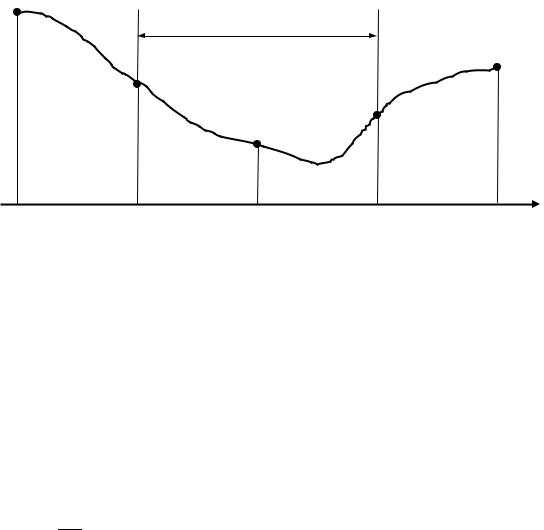
В этом методе интервал [a,b] делится на несколько равных частей с последующим вычислением значений функции в узлах полученной сетки. В качестве минимума принимается абсцисса с минимальным вычисленным значением функции (рис. 4).
11
D
Рис. 4. Иллюстрация к метлду общего поиска
В результате интервал неопределенности сужается до двух шагов сетки. Обычно говорят о дроблении интервала неопределенности, которое харак-
теризуется коэффициентом α. Разделив интервал неопределенности наn равных
частей, получим n+1 узел. Тогдаα = | 2 | . При этом необходимо вычислить функ- | |||
цию N = n+1 раза. Следовательно, | n |
| |||
|
| ||||
α = | 2 |
| , N = 3,4,5... |
| (2.1) |
N −1 |
| ||||
|
|
|
| ||
Чтобы получить значение α = 0.01 потребуется вычислить функцию в 201 точке, а приα=0.001N=2001. Ясно, что эффективность этого метода с уменьшением интервала неопределенности быстро падает.
2.1.2. Унимодальные функции
Более эффективные методы можно построить, если предположить, что исследуемая функция имеет в рассматриваемом интервале только один минимум. Более точно: предположим, что в интервале [a,b] имеется единственное значе-
ние x* такое, чтоf (x*) – минимумf (x) на [a,b] и чтоf (x) строго убывает для
x ≤ x* и строго возрастает дляx ≥ x* (рис. 5). Такая функция называется унимодальной.
Для ее графика имеются три различные формы:
Рис. 5. Унимодальные функции
12
Заметим, что унимодальная функция не обязана быть гладкой или даже непрерывной.
Из предположения унимодальности следует, что для любых точек x1,x2
интервала [a,b], | таких, что | x | < x | ≤ x* справедливо | f (x) < f(x) . | Аналогично, | |||
|
|
| 1 | 2 |
|
| 2 | 1 |
|
если x* ≤ x < x , | то f (x )> f (x ) . | Обратно, если | x < x | и f (x )> f (x ) , то | |||||
1 | 2 | 2 |
| 1 |
| 1 | 2 | 1 | 2 |
x ≤ x* ≤ b, а если | f (x )< f (x ) , тоa ≤ x* ≤ x . Далее будем считать исследуемую | ||||||||
1 |
| 1 | 2 |
| 2 |
|
|
|
|
функцию унимодальной.
2.1.3. Метод деления интервала пополам
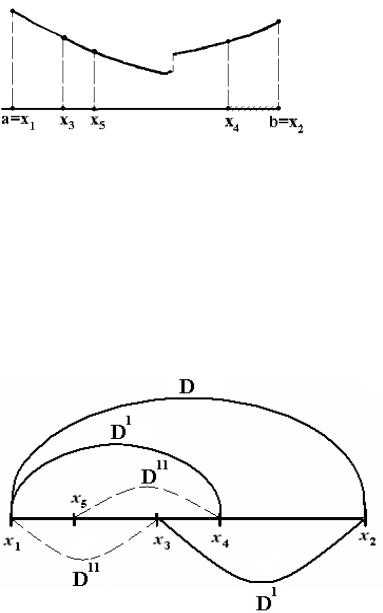
Разделим интервал [a,b] на две равные части (рис. 6), а затем каждую из частей еще на две равные части.
D
Рис. 6. Иллюстрация к методу половинного деления
Это первый этап поиска минимума. На нем после пяти вычислений функции (два – на краях и три – внутри интервала [a,b]) интервал неопределенности сужается вдвое, то есть на этом этапеα = 0,5. Новый интервал неопределенно-
сти [x4 ,x5 ] снова разделим пополам, а затем каждую половину снова пополам.
Теперь значения функции по краям и в его середине уже известны. Поэтому для завершения поиска на этом этапе требуется вычислить только два значения функции, после чего интервал неопределенности снова уменьшится вдвое. Это преимущество рассмотренного метода сохранится и в дальнейшем.
После N вычислений функции коэффициент дробления интервала состав-
ляет
Здесь N=5,7,9,…, так как интервал неопределенности, начиная со второго этапа, уменьшается только после двух вычислений функции.
Из (2.1),(2.2) видно, что метод деления пополам эффективнее, чем общий поиск.
13
2.1.4. Метод золотого сечения
Деление интервала на неравные части позволяет найти еще более эффек-
тивный | метод. Вычислим функцию на | концах | отрезка [a,b] | и положим | ||
a = x1, | b = x2. | Вычислим также | функцию | в двух | внутренних точках x3,x4. | |
Сравним все | четыре значения | функции | и выберем среди них | наименьшее | ||
(рис.°7). Пусть, например, наименьшим оказалось f(x3). Очевидно, минимум находится в одном из прилегающих к нему отрезков. Поэтому отрезок[x4,b]
можно отбросить и оставить отрезок [a,x4 ].
Рис. 7. Иллюстрация к методу золотого сечения
Первый шаг сделан. На отрезке [a,x4 ] снова надо выбрать две внутрен-
ние точки, вычислив в них и на концах значения функции и сделать следующий шаг. Но на предыдущем шаге вычислений мы уже нашли функцию на концах
нового отрезка [a,x4 ] и в одной его внутренней точ кеx3 . Потому достаточно выбрать внутри[a,x4 ] еще одну точкуx5, определить в ней значение функции
и провести необходимые сравнения. Это вчетверо уменьшает объем вычислений на одном шаге процесса. Как выгодно размещать точки? Каждый раз оставшийся отрезок делится на три части и затем отбрасывается один из крайних отрезков.
Обозначим первоначальный интервал неопределенности через D (рис. 8).
Рис. 8. Деление интервала в методе золотого сечения
Так как в общем случае может быть отброшен любой из отрезков x1x3 илиx4x2 , то выберем точкиx3 иx4 так, чтобы длины этих отрезков были одинаковы:x3 − x1 = x2 − x4. После отбрасывания получится новый интервал неопределенности длиныD′.
14

Обозначим отношение D буквойϕ:
D′
ϕ = DD′.
Далее продолжим процесс аналогично. Для этого интервал D′ разделим подобно интервалуD, то есть положимDD′′′ = DD′ = ϕ, гдеD′′– следующий интер-
вал неопределенности (иногда такое деление интервала называют делением в крайнем и среднем отношении: весь интервал относится к бóльшей части, как бóльшая часть к меньшей). Но D′′ по длине равен отрезку, отброшенному на предыдущем этапе, то естьD′′ = D − D′. Поэтому получим:
DD′ = DD−′D′ DD′ = DD′ −1.
Это приводит к уравнению ϕ1 = ϕ−1 или, что то же
ϕ2 −ϕ−1 =0 .
Положительный корень этого уравнения дает
ϕ = 52+1 ≈1,6180.
Последнее число известно в математике как золотое отношение, а описанное деление отрезка, как золотое сечение. Потому рассматриваемый метод поис-
ка минимума называют методом золотого сечения. Отношение DD′ = ϕ ≈1,618
показывает, во сколько раз сокращается интервал неопределенности при одном добавочном вычислении функции. Учтем, что первые три вычисления еще не сокращают интервал неопределенности. Поэтому после N вычислений функции коэффициент дробления будет
| 1 | N −3 |
| |
α = |
|
| ≈ (0,6180)N −3 . | (2.3) |
| ||||
| ϕ |
|
| |
При N → ∞ длина интервала неопределенности стремится к нулю как геометрическая прогрессия со знаменателемϕ1 , то есть метод золотого сечения
всегда сходится. Очевидно, этот метод более эффективен, чем метод деления пополам, так как после N вычислений функции длина интервала неопределенно-
сти уменьшается при золотом сечении в ϕN −3 ≈ (1,6180)N −3 раз, а в методе деле-
n−3
ния пополам в 2 2 ≈ (1,4142)N −3 раза.
15

Приведем теперь вычислительную схему метода. Имеем |
| D | = ϕ, причем | |||||||||||||||||||||||
| ′ | |||||||||||||||||||||||||
D = x2 − x1, | D′ =x4 −x1 или x2 −x3 . |
|
|
|
| D |
| |||||||||||||||||||
|
|
|
|
|
| |||||||||||||||||||||
Поэтому |
| x2− x1 | = ϕ, |
| x2− x1 |
| = ϕ, |
|
|
|
|
|
|
| ||||||||||||
|
| x − x |
|
|
|
|
|
|
| |||||||||||||||||
|
|
| x | − x |
|
|
|
|
|
|
|
|
|
|
| |||||||||||
что дает |
|
|
| 2 |
| 3 |
| 4 |
| 1 |
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
| 1 |
|
|
|
|
|
|
| −1 | (x |
|
|
|
|
| ||||||||||
x | = x − | (x | − x ) =x − |
|
| 5 | − x ) ≈x | −0,6180(x | − x ) | , | (2.4) | |||||||||||||||
4 |
|
|
|
|
|
| ||||||||||||||||||||
3 | 2 |
| 2 | 1 | 2 |
| 2 | 2 | 1 | 2 | 2 | 1 |
|
|
| |||||||||||
|
| 1 |
|
|
|
|
| −1 | (x |
|
|
|
|
| ||||||||||||
x | = x + | (x | − x ) =x + |
|
| 5 | − x )≈ x + 0,6180(x | − x ) . |
|
| (2.5) | |||||||||||||||
4 |
|
|
|
|
|
|
| |||||||||||||||||||
4 | 1 |
| 2 | 1 | 1 |
| 2 | 2 | 1 | 1 | 2 | 1 |
|
|
| |||||||||||
Так как длины отрезков x1x3 иx4x2 равны, последнее равенство можно переписать следующим образом:
После сравнения может быть отброшена точка с любым номером, так что на следующих шагах оставшиеся точки будут перенумерованы беспорядочно. Пусть на данном отрезке есть четыре точки, xi ,xj ,xk ,xl , из которыхкакие-то
две являются концами отрезка.
Выберем ту точку, в которой функция принимает наименьшее значение; пусть это оказалась точка xi :
f (xi )< f (xj ),f (xk ),f (xl ) | (2.7) |
Затем отбрасываем ту точку, которая более удалена от хi (это верно в методе золотого сечения). Пусть этой точкой оказаласьxl :
xl− xi> xj− xi, xk− xi.
Определим порядок распределения оставшихся трех точек на числовой оси; пусть, например, xk < xi < xj . Пронумеруем эти точки, положивk=1, j=2,
i=3. Тогда новую внутреннюю точку введем по формуле (2.6):x4 = x1 + x2 − x3 .
Ее номер теперь – 4.
Вычислим функцию f (x4 ) в этой точке. Выполним сравнение, отбросим
одну точку, заново переименуем точки, введем новую точку по формуле (2.6) и т.д.
Минимум находится где-товнутри последнего отрезка:x* [x1,x2 ]. По-
этому процесс прекращается, когда длина этого интервала неопределенности станет меньше заданной погрешности: x2 − x1 < ε.
Заметим, что если на [а,b] функция имеет несколько минимумов, то процесс сойдется к одному из них, но не обязательно к наименьшему.
16
studfiles.net
НОУ ИНТУИТ | Лекция | Однопараметрическая (одномерная) оптимизация. Методы одномерной оптимизации: метод дихотомии, метод Фибоначчи, метод "золотого сечения", метод Ньютона.
Аннотация: Данная лекция рассматривает задачи однопараметрической оптимизации и приводит наиболее распространенные методы решения этих задач, в частности, такие как метод дихотомии, метод Фибоначчи, метод "золотого сечения", метод Ньютона; также формулируются их основные характеристики, определяется область применения и выясняются преимущества и недостатки данных методов.
Однопараметрическая оптимизация (поиск экстремумов функций одной переменной) является самостоятельной и часто встречаемой задачей. Кроме того, к ней сводится гораздо более сложная задача - поиск экстремума функции многих переменных.
1. Метод дихотомии.
Рассмотрим простейший однопараметрический метод безусловной оптимизации – метод дихотомии. Этот метод является методом прямого поиска. В нем при поиске экстремума целевой функции используются только вычисленные значения целевой функции.
Дана функция F(x). Необходимо найти , доставляющий минимум (или максимум) функции F(x) на интервале [a,b] с заданной точностью , т.е. найти
Запишем словесный алгоритм метода.
1) На каждом шаге процесса поиска делим отрезок [a,b] пополам, x=(a+b)/2 - координата середины отрезка [a,b].
2) Вычисляем значение функции F(x) в окрестности вычисленной точки x, т.е.
3) Сравниваем F1 и F2 и отбрасываем одну из половинок отрезка [a,b] (рис. 9.1).
При поиске минимума:
Если F1<F2, то отбрасываем отрезок [x,b], тогда b=x. (рис. 9.1.а)
Иначе отбрасываем отрезок [a,x], тогда a=x. (рис. 9.1.б)
При поиске максимума:
Если F1<F2, то отбрасываем отрезок [a,x], тогда a=x.
Иначе отбрасываем отрезок [x,b], тогда b=x.
4) Деление отрезка [a,b] продолжается, пока его длина не станет меньше заданной точности , т.е.
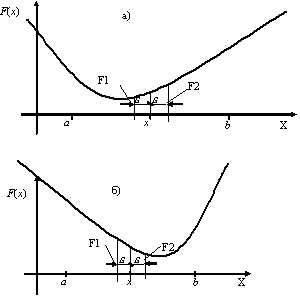 Рис. 9.1. Поиск экстремума функции F(x) методом дихотомии
Рис. 9.1. Поиск экстремума функции F(x) методом дихотомииСхема алгоритма метода дихотомии представлена на рис 9.2.
На рис 9.2: c - константа,
При выводе x – координата точки, в которой функция F(x) имеет минимум (или максимум), FM – значение функции F(x) в этой точке.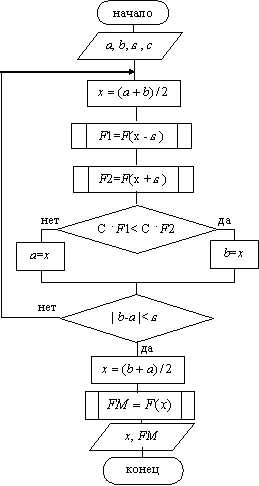 Рис. 9.2. Схема алгоритма метода дихотомии
Рис. 9.2. Схема алгоритма метода дихотомииwww.intuit.ru
НОУ ИНТУИТ | Лекция | Однопараметрическая (одномерная) оптимизация. Методы одномерной оптимизации: метод дихотомии, метод Фибоначчи, метод "золотого сечения", метод Ньютона.
Аннотация: Данная лекция рассматривает задачи однопараметрической оптимизации и приводит наиболее распространенные методы решения этих задач, в частности, такие как метод дихотомии, метод Фибоначчи, метод "золотого сечения", метод Ньютона; также формулируются их основные характеристики, определяется область применения и выясняются преимущества и недостатки данных методов.
Однопараметрическая оптимизация (поиск экстремумов функций одной переменной) является самостоятельной и часто встречаемой задачей. Кроме того, к ней сводится гораздо более сложная задача - поиск экстремума функции многих переменных.
1. Метод дихотомии.
Рассмотрим простейший однопараметрический метод безусловной оптимизации – метод дихотомии. Этот метод является методом прямого поиска. В нем при поиске экстремума целевой функции используются только вычисленные значения целевой функции.
Дана функция F(x). Необходимо найти , доставляющий минимум (или максимум) функции F(x) на интервале [a,b] с заданной точностью , т.е. найти
Запишем словесный алгоритм метода.
1) На каждом шаге процесса поиска делим отрезок [a,b] пополам, x=(a+b)/2 - координата середины отрезка [a,b].
2) Вычисляем значение функции F(x) в окрестности вычисленной точки x, т.е.
3) Сравниваем F1 и F2 и отбрасываем одну из половинок отрезка [a,b] (рис. 9.1).
При поиске минимума:
Если F1<F2, то отбрасываем отрезок [x,b], тогда b=x. (рис. 9.1.а)
Иначе отбрасываем отрезок [a,x], тогда a=x. (рис. 9.1.б)
При поиске максимума:
Если F1<F2, то отбрасываем отрезок [a,x], тогда a=x.
Иначе отбрасываем отрезок [x,b], тогда b=x.
4) Деление отрезка [a,b] продолжается, пока его длина не станет меньше заданной точности , т.е.
 Рис. 9.1. Поиск экстремума функции F(x) методом дихотомии
Рис. 9.1. Поиск экстремума функции F(x) методом дихотомииСхема алгоритма метода дихотомии представлена на рис 9.2.
На рис 9.2: c - константа,
При выводе x – координата точки, в которой функция F(x) имеет минимум (или максимум), FM – значение функции F(x) в этой точке. Рис. 9.2. Схема алгоритма метода дихотомии
Рис. 9.2. Схема алгоритма метода дихотомииwww.intuit.ru
оптимизация
Лекция 1
Оптимизация - процесс выбора наилучшего варианта из всех возможных. В процессе решения задачи оптимизации обычно необходимо найти оптимальные значения параметров, определяющих данную задачу. Их называют проектными параметрами. Выбор оптимального решения или сравнения двух альтернативных решений проводится с помощью некоторой зависимой величины, определяемой проектными параметрами. Эта величина называется целевой функцией. Если целевая функция зависит от одного проектного параметра, то мы имеем одномерную задачу оптимизации.
Цель одномерной оптимизации – определение минимума (или максимума) функции одной переменной, заданной на интервале изменения аргумента. Предположим, что функция на отрезке 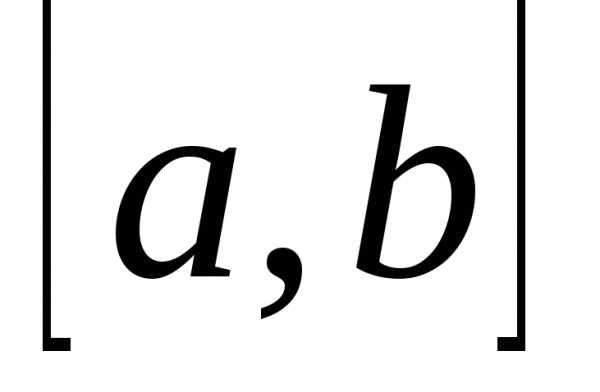 унимодальная, т. е. на данном отрезке она имеет только один минимум.
унимодальная, т. е. на данном отрезке она имеет только один минимум.
Процесс решения задачи состоит в последовательном сужении интервала изменения параметра, называемого интервалом неопределенности. В начале процесса оптимизации его длина равна  , а к концу она должна стать менее заданного допустимого значения
, а к концу она должна стать менее заданного допустимого значения .
.
Метод дихотомии
Метод дихотомии несколько схож с методом бисекции, однако отличается от него критерием отбрасывания концов.
Пусть задана функция . Разобьём мысленно заданный отрезок пополам и возьмём две симметричные относительно центра точкиитак, что:
где — некоторое число в интервале(0; (b–a)/2).
Вычислим значения функции в двух новых точках. Сравнением определим, в какой из двух новых точек значение функциимаксимально. Отбросим тот из концов изначального отрезка, к которому точка с максимальным значением функции оказалась ближе (напомним, мы ищемминимум), то есть:
Процедура повторяется, пока не будет достигнута заданная точность, к примеру, пока длина отрезка не достигнет удвоенного значения заданной погрешности.
2. Метод золотого сечения
При построении процесса оптимизации стараются сократить объем вычислений и время поиска. Одним из наиболее эффективных методов является метод золотого сечения. Он состоит в построении последовательности отрезков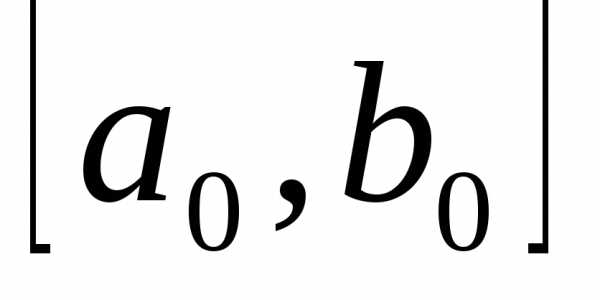 ,
,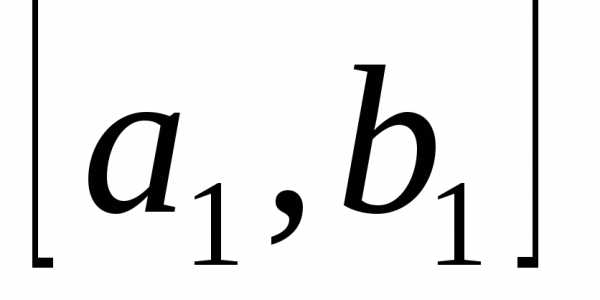 , …, стягивающихся к точке минимума функции. На каждом шаге, за исключением первого, вычисление значения функции производится один раз в точке, называемой золотым сечением. Золотое сечение интервала выбирается так, чтобы отношение длины большего отрезка
, …, стягивающихся к точке минимума функции. На каждом шаге, за исключением первого, вычисление значения функции производится один раз в точке, называемой золотым сечением. Золотое сечение интервала выбирается так, чтобы отношение длины большего отрезка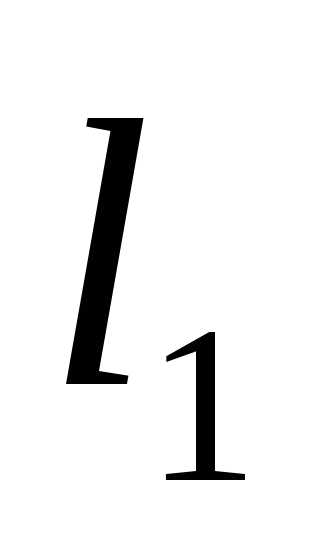 к длине всего интервала
к длине всего интервала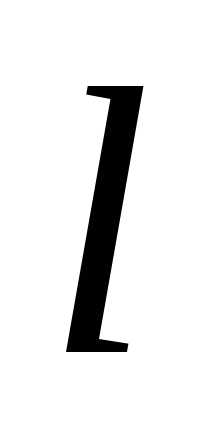 равнялось отношению длины меньшего отрезка
равнялось отношению длины меньшего отрезка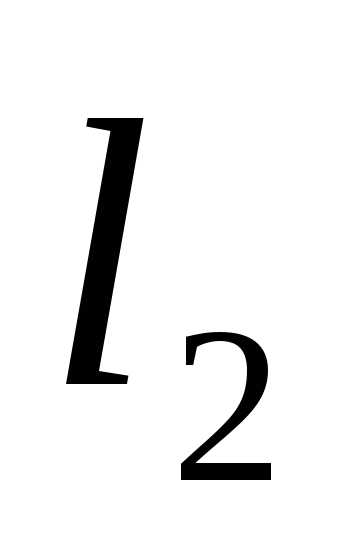 к длине большего отрезка
к длине большего отрезка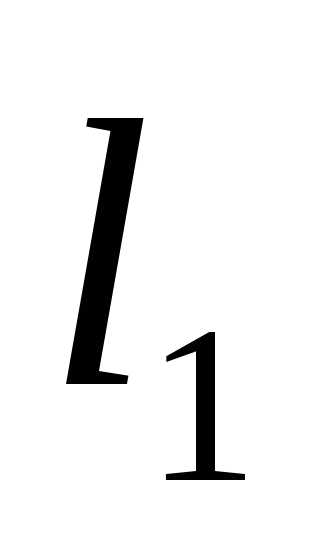 :
:
,
Из этого соотношения можно найти точку деления:
Так как нас интересует только положительное решение, то
Отсюда
Поскольку заранее неизвестно в какой последовательности (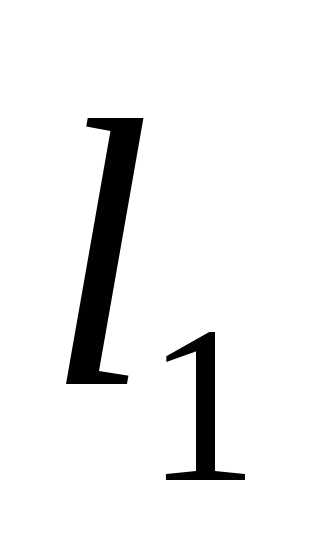 и
и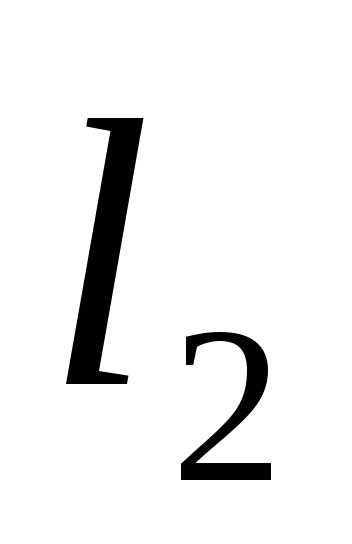 или
или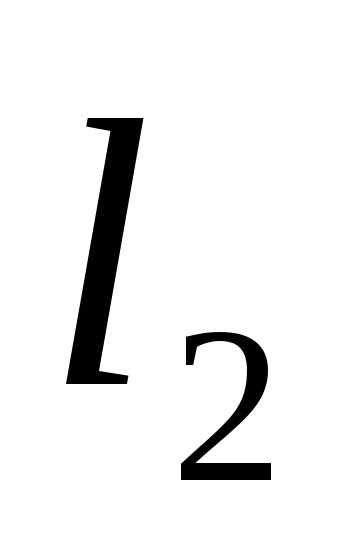 и
и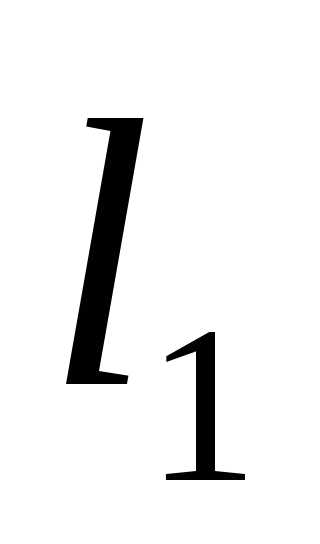 ) делить интервал неопределенности, то рассматривают внутренние точки, соответ-ствующие двум этим способам деления.
) делить интервал неопределенности, то рассматривают внутренние точки, соответ-ствующие двум этим способам деления.
Точки 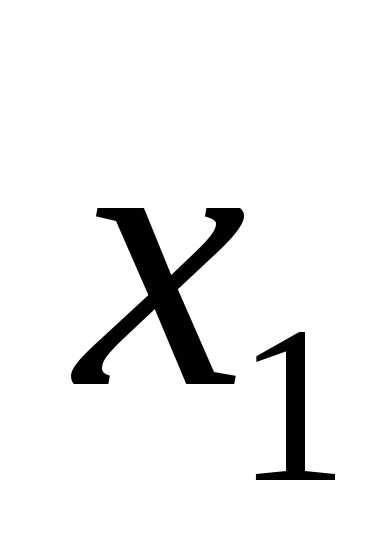 и
и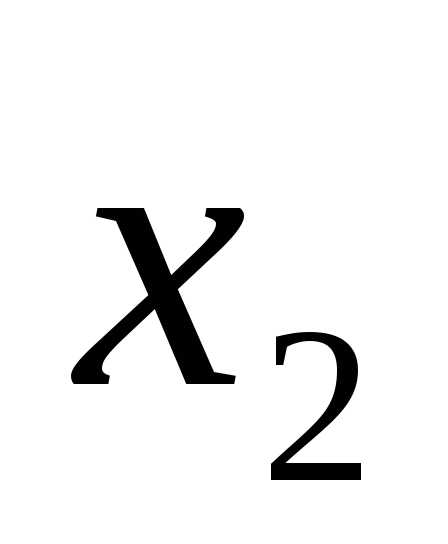 выбирают с учетом полученных значений частей отрезка. В данном случае:
выбирают с учетом полученных значений частей отрезка. В данном случае:
После первого шага оптимизации получается новый интервал неопределенности 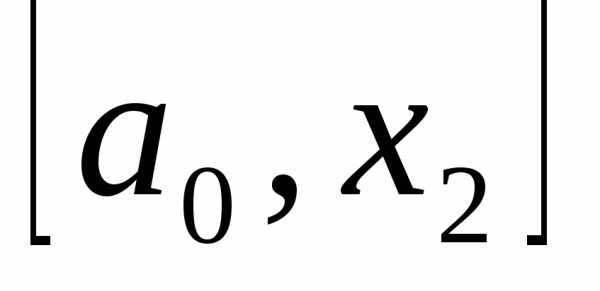 . Точка
. Точка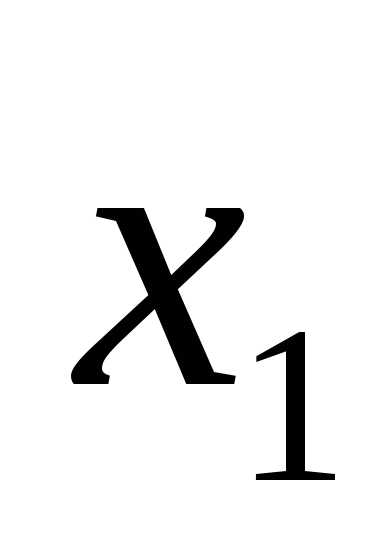 делит этот отрезок в требуемом отношении, т. е.
делит этот отрезок в требуемом отношении, т. е.
Вторая точка 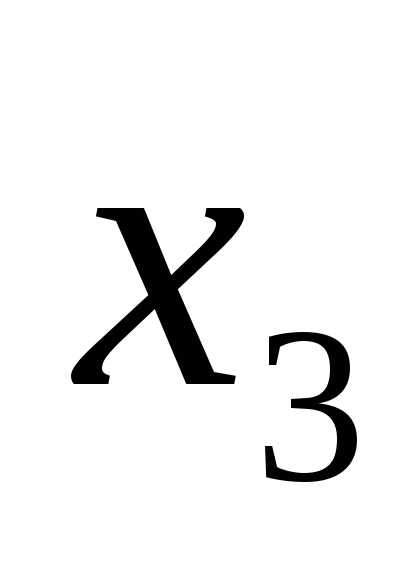 выбирается на таком же расстоянии от левой границы отрезка, т.е.
выбирается на таком же расстоянии от левой границы отрезка, т.е.
И снова интервал неопределенности уменьшается до величины
Используя полученные соотношения, можно записать координаты точек деления  и
и на отрезке
на отрезке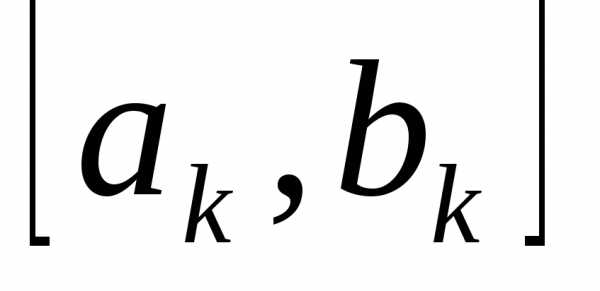 на
на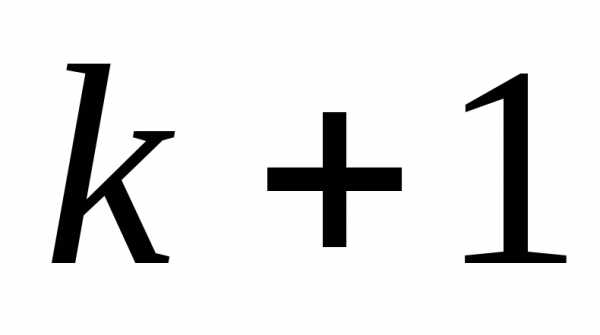 шаге:
шаге:
При этом длина интервала неопределенности равна:
Процесс оптимизации заканчивается при выполнении условия
Метод Фибоначчи
Метод Фибоначчи –разновидностьодномерногопоискаэкстремумафункциипутемпоследовательногосуженияинтерваланеопределенности.Единственноеограничение,налагаемоенаисследуемуюфункциюf(x)–требованиестрогойунимодальностиназаданноминтервале.
Припоследовательномсужениизначенияf(x) вычисляются(илизамеряются)взаранееограниченномчислепробныхточек.Врезультатеполучаетсяпоследовательностьсужающихсяинтерваловнеопределенности,содержащихискомыйэкстремум:
Чтобы сузить интервал неопределенности для произвольной строго унимодальной функции, нужно знать не менее двух ее пробных значений. В методе Фибоначчи внутри каждого текущего интервала неопределенности (ai, bi) подбираются ровно две пробные точки симметрично от середины интервала. Далее, от одной из пробных точек отбрасывается конец интервала с наихудшими значениями f(x). Получается ( а i+1 , bi+1), где в дополнение к оставшейся старой пробной точке симметрично строится новая. Отсюда для длин интервалов следует рекуррентное уравнение
(Помимо прочего выше предполагалось, что выполнено условие перекрывания Решение уравнения при условии дает
где –числа Фибоначчи:
F0 = 0, F1 = 1, Fn = Fn –1+ Fn –2 .
Точка экстремума
В простейшем варианте метода Фибоначчи (когда предполагается, что пробные точки и пробные значения f(x)определяются абсолютно точно), чтобы сузить исходный интервал неопределенности с до надо взять число пробных точек из неравенства
4. Методы с использованием информации о производной функции
В методах прямого поиска при вычислении значений минимизируемой функции f(x) неизбежно возникают погрешности, к которым чувствительны алгоритмы прямого поиска, основанные на сравнении значений функции в отдельных точках. Если унимодальная функцияf(x) непрерывно дифференцируема на отрезке минимизации, то точкух* наименьшего значения функции можно вычислять как корень уравнения:
f (x) = 0
с помощью тех или иных методов численного решения нелинейных уравнений. В этом случае на точность решения задачи решающее влияние оказывает погрешность вычисления производной функции. Рассмотрим некоторые методы одномерной минимизации, основанные на использовании производной минимизируемой функции.
4.1. Метод Ньютона (метод касательных). Если строго унимодальная на отрезке [a, b] функцияf(x) дважды непрерывно дифференцируема на этом отрезке, то точкуx* минимума этой функции можно найти путем решения уравненияf (x) = 0 методом Ньютона, иногда называемым методом касательных. Выбираемx0 начальное приближение, называемое обычно начальной точкой. Линеаризуем функциюf(x) в окрестности начальной точки, приближенно заменив дугу графика этой функции касательной в точке (x0,f (x0)). Выберем в качестве следующего приближения кх* точкуx1пересечения касательной с осью абсцисс.
В общем случае сходимость метода Ньютона существенно зависит от выбора начальной точки x0. Поэтому говорят, что метод Ньютона обладает локальной сходимостью в том смысле, что надо выбрать хорошее начальное приближение, попадающее в такую окрестность точких*, гдеf ''(x) > 0. Однако проверка выполнения этого условия не всегда возможна. Достаточным условием монотонной сходимости метода Ньютона будут постоянство в интервале между точкамиx0их* знака производнойf ''' (x) и совпадение его со знакомf' (x). Оказывается, что в этом случае метод Ньютона обладает квадратичной скоростью сходимости в некоторой окрестности точких*.
4.2. Метод секущих. Метод секущих похож на метод Ньютона, но строится не касательная к графику производной, а секущая. Геометрическая интерпретация этого метода состоит в том, что в качестве очередного приближенияxk+1выбирают точку пересечения с осью абсцисс секущей к графику функцииf ' (x).
Этот метод имеет сверхлинейную скорость сходимости. Модификации метода Ньютона обладают только локальной сходимостью, т.е. сходятся, если начальная точка выбрана в некоторой окрестности точки минимума функции. Если же начальная точка расположена слишком далеко от точки минимума, то подобный метод может расходиться или «зацикливаться». В отличие от метода средней точки метод секущих использует информацию не только о знаке производной, но и о значениях в пробных точках.
Лабораторная работа № 5
Задания:
для заданной функции определить интервал, на котором она унимодальная;
методом золотого сечения найти минимум функции и сравнить его с точным значением (ε = 10-3).
Данные к заданию:
| № варианта | Задание |
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 | |
| 6 |
|
| 7 |
|
| 8 | |
| 9 |
|
| 10 | |
| 11 |
|
| 12 |
|
Б.П. Демидович, И.А. Марон. Основы вычислительной математики – М.: Наука, 1970.
Л.И. Турчак. Основы численных методов – М.: Наука, 1987.
Г.Н. Воробьева, А.Н. Данилова. Практикум по вычислительной математике. – М.: Высшая школа, 1990.
В.М. Заварыкин, В.Ч. Житомирский, М.П. Лапчик. Численные методы – М.: Просвещение, 1990.
Е. А. Волков. Численные методы. – М.: Наука, 1982.
Г.И. Марчук. Методы вычислительной математики. – М.: Наука, 1980.
Р.В. Хемминг. Численные методы. – М.: Наука,1968.
Н.С. Бахвалов. Численные методы. – М.: Наука, 1973.
6
studfiles.net
НОУ ИНТУИТ | Лекция | Однопараметрическая (одномерная) оптимизация. Методы одномерной оптимизации: метод дихотомии, метод Фибоначчи, метод "золотого сечения", метод Ньютона.
Аннотация: Данная лекция рассматривает задачи однопараметрической оптимизации и приводит наиболее распространенные методы решения этих задач, в частности, такие как метод дихотомии, метод Фибоначчи, метод "золотого сечения", метод Ньютона; также формулируются их основные характеристики, определяется область применения и выясняются преимущества и недостатки данных методов.
Однопараметрическая оптимизация (поиск экстремумов функций одной переменной) является самостоятельной и часто встречаемой задачей. Кроме того, к ней сводится гораздо более сложная задача - поиск экстремума функции многих переменных.
1. Метод дихотомии.
Рассмотрим простейший однопараметрический метод безусловной оптимизации – метод дихотомии. Этот метод является методом прямого поиска. В нем при поиске экстремума целевой функции используются только вычисленные значения целевой функции.
Дана функция F(x). Необходимо найти , доставляющий минимум (или максимум) функции F(x) на интервале [a,b] с заданной точностью , т.е. найти
Запишем словесный алгоритм метода.
1) На каждом шаге процесса поиска делим отрезок [a,b] пополам, x=(a+b)/2 - координата середины отрезка [a,b].
2) Вычисляем значение функции F(x) в окрестности вычисленной точки x, т.е.
3) Сравниваем F1 и F2 и отбрасываем одну из половинок отрезка [a,b] (рис. 9.1).
При поиске минимума:
Если F1<F2, то отбрасываем отрезок [x,b], тогда b=x. (рис. 9.1.а)
Иначе отбрасываем отрезок [a,x], тогда a=x. (рис. 9.1.б)
При поиске максимума:
Если F1<F2, то отбрасываем отрезок [a,x], тогда a=x.
Иначе отбрасываем отрезок [x,b], тогда b=x.
4) Деление отрезка [a,b] продолжается, пока его длина не станет меньше заданной точности , т.е.
 Рис. 9.1. Поиск экстремума функции F(x) методом дихотомии
Рис. 9.1. Поиск экстремума функции F(x) методом дихотомииСхема алгоритма метода дихотомии представлена на рис 9.2.
На рис 9.2: c - константа,
При выводе x – координата точки, в которой функция F(x) имеет минимум (или максимум), FM – значение функции F(x) в этой точке. Рис. 9.2. Схема алгоритма метода дихотомии
Рис. 9.2. Схема алгоритма метода дихотомииwww.intuit.ru
НОУ ИНТУИТ | Лекция | Однопараметрическая (одномерная) оптимизация. Методы одномерной оптимизации: метод дихотомии, метод Фибоначчи, метод "золотого сечения", метод Ньютона.
Аннотация: Данная лекция рассматривает задачи однопараметрической оптимизации и приводит наиболее распространенные методы решения этих задач, в частности, такие как метод дихотомии, метод Фибоначчи, метод "золотого сечения", метод Ньютона; также формулируются их основные характеристики, определяется область применения и выясняются преимущества и недостатки данных методов.
Однопараметрическая оптимизация (поиск экстремумов функций одной переменной) является самостоятельной и часто встречаемой задачей. Кроме того, к ней сводится гораздо более сложная задача - поиск экстремума функции многих переменных.
1. Метод дихотомии.
Рассмотрим простейший однопараметрический метод безусловной оптимизации – метод дихотомии. Этот метод является методом прямого поиска. В нем при поиске экстремума целевой функции используются только вычисленные значения целевой функции.
Дана функция F(x). Необходимо найти , доставляющий минимум (или максимум) функции F(x) на интервале [a,b] с заданной точностью , т.е. найти
Запишем словесный алгоритм метода.
1) На каждом шаге процесса поиска делим отрезок [a,b] пополам, x=(a+b)/2 - координата середины отрезка [a,b].
2) Вычисляем значение функции F(x) в окрестности вычисленной точки x, т.е.
3) Сравниваем F1 и F2 и отбрасываем одну из половинок отрезка [a,b] (рис. 9.1).
При поиске минимума:
Если F1<F2, то отбрасываем отрезок [x,b], тогда b=x. (рис. 9.1.а)
Иначе отбрасываем отрезок [a,x], тогда a=x. (рис. 9.1.б)
При поиске максимума:
Если F1<F2, то отбрасываем отрезок [a,x], тогда a=x.
Иначе отбрасываем отрезок [x,b], тогда b=x.
4) Деление отрезка [a,b] продолжается, пока его длина не станет меньше заданной точности , т.е.
 Рис. 9.1. Поиск экстремума функции F(x) методом дихотомии
Рис. 9.1. Поиск экстремума функции F(x) методом дихотомииСхема алгоритма метода дихотомии представлена на рис 9.2.
На рис 9.2: c - константа,
При выводе x – координата точки, в которой функция F(x) имеет минимум (или максимум), FM – значение функции F(x) в этой точке. Рис. 9.2. Схема алгоритма метода дихотомии
Рис. 9.2. Схема алгоритма метода дихотомииwww.intuit.ru
НОУ ИНТУИТ | Лекция | Однопараметрическая (одномерная) оптимизация. Методы одномерной оптимизации: метод дихотомии, метод Фибоначчи, метод "золотого сечения", метод Ньютона.
Аннотация: Данная лекция рассматривает задачи однопараметрической оптимизации и приводит наиболее распространенные методы решения этих задач, в частности, такие как метод дихотомии, метод Фибоначчи, метод "золотого сечения", метод Ньютона; также формулируются их основные характеристики, определяется область применения и выясняются преимущества и недостатки данных методов.
Однопараметрическая оптимизация (поиск экстремумов функций одной переменной) является самостоятельной и часто встречаемой задачей. Кроме того, к ней сводится гораздо более сложная задача - поиск экстремума функции многих переменных.
1. Метод дихотомии.
Рассмотрим простейший однопараметрический метод безусловной оптимизации – метод дихотомии. Этот метод является методом прямого поиска. В нем при поиске экстремума целевой функции используются только вычисленные значения целевой функции.
Дана функция F(x). Необходимо найти , доставляющий минимум (или максимум) функции F(x) на интервале [a,b] с заданной точностью , т.е. найти
Запишем словесный алгоритм метода.
1) На каждом шаге процесса поиска делим отрезок [a,b] пополам, x=(a+b)/2 - координата середины отрезка [a,b].
2) Вычисляем значение функции F(x) в окрестности вычисленной точки x, т.е.
3) Сравниваем F1 и F2 и отбрасываем одну из половинок отрезка [a,b] (рис. 9.1).
При поиске минимума:
Если F1<F2, то отбрасываем отрезок [x,b], тогда b=x. (рис. 9.1.а)
Иначе отбрасываем отрезок [a,x], тогда a=x. (рис. 9.1.б)
При поиске максимума:
Если F1<F2, то отбрасываем отрезок [a,x], тогда a=x.
Иначе отбрасываем отрезок [x,b], тогда b=x.
4) Деление отрезка [a,b] продолжается, пока его длина не станет меньше заданной точности , т.е.
 Рис. 9.1. Поиск экстремума функции F(x) методом дихотомии
Рис. 9.1. Поиск экстремума функции F(x) методом дихотомииСхема алгоритма метода дихотомии представлена на рис 9.2.
На рис 9.2: c - константа,
При выводе x – координата точки, в которой функция F(x) имеет минимум (или максимум), FM – значение функции F(x) в этой точке. Рис. 9.2. Схема алгоритма метода дихотомии
Рис. 9.2. Схема алгоритма метода дихотомииwww.intuit.ru