Расчётно-пояснительная записка. Для решения задач линейной оптимизации можно использовать следующий математический аппарат
Mat_progr_-_testy - Стр 2
Если в задаче на min все оценки Sij свободных клеток ≥ 0, то:
а) план оптимален ДА
б) плане не оптимален
в) план является опорным
г) план является начальным
Если в опорном решении транспортной задачи число отличных от нуля неизвестных равно m+n-1, то решение называется:
а) вырожденным; б) невырожденным
Если в транспортной задаче суммарный запас груза у поставщиков больше суммарного спроса потребителей, то:
а) необходимо уменьшить спросы потребителей; б) для разрешимости задачи необходимо вести фиктивного потребителя;в) задача не имеет решения; г) для разрешимости задачи необходимо вести фиктивного поставщика.
Если X* - оптимальный план исходной (прямой) задачи с ……….. f(x) 5X1 + 7X2; а y* - оптимальный план двойственной к ней с целевой функцией F(y) = 20у1 + 40у2 + 25у2, то пара……..
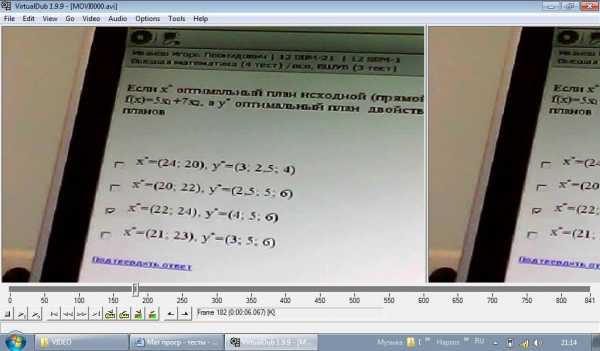
вариант В (НЕТ)
Если в транспортной задаче суммарный запас груза у поставщиков меньше суммарного спроса потребителей, то:
а) задача не имеет решения;
б) для разрешимости задачи необходимо ввести фиктивного поставщика;
в) для разрешимости задачи необходимо ввести фиктивного потребителя;
г) необходимо уменьшить опросы потребителей.
Если в f-строке симплексной таблицы задачи линейного программирования есть отрицательный элемент, которому соответствует столбец, не содержащий ни одного положительного элемента, то:
а) целевая функция непрерывная; б) целевая функция неограниченна;в) задача имеет бесконечное множество оптимальных планов.
Если в строке симплексной таблицы задачи линейной оптимизации есть отрицательный элемент и все элементы столбца, в котором он находится, неположительные,то:
а) целевая функция неограничена;
б) целевая функция четная;
в) целевая функция непрерывная.
Если в f-строке симплексной таблицы, содержащей оптимальный план, есть хотя бы один нулевой элемент, то:
а) задача имеет единственное решение; б) задача не имеет решения; в) решение задачи не завершено; г) задача имеет множество оптимальных решений
Если число отличных от нуля объемов перевозок в решении транспортной задачи равно т+ п-1, то это решение называют:
а) вырожденным;
б) невырожденным;
в) открытым;
г) закрытым.
Если значение потенциала U2 = 1, то значение потенциала V3 будет равно
|
| ||||||||||||||||||||||||||||||||||||
Если найдено опорное решение транспортной задачи:
а) то для каждой свободной клетки этого решения можно образовать единственный цикл;
б) то для каждой свободной клетки можно образовать множество циклов;
в) то для каждой занятой клетки можно образовать единственный цикл.
Если в строке оптимального решения задачи линейной оптимизации есть хотя бы один нулевой элемент, то:
а) задача имеет множество оптимальных решений;
б) задача не имеет решений;
в) задача имеет единственное решение;
г) решение задачи не завершено.
Если целевая функция одной из взаимо двойственных задач не ограничена, то
а) в другой задаче целевая функция тоже не ограничена; б) другая задача не имеет решения;в) другая задача имеет единственное решение.
Если Х* оптимальный план исходной (прямой) задачи с целевой функцией f(x)= 6х1+4х2, а y – оптимальный план двойственной к ней с целевой функцией F(y) = 20у1+40у2+25у3, то пара оптимальных планов:
а) Х*= (25;20) Y*= (3;6;4)
б) Х*= (20;25) Y*= (2;2;4) ДА
в) Х*= (22;10) Y*= (4;5;6)
г) Х*= (21;23) Y*= (3;5;6)
Если х1, х2,х3 , х4 булевы переменные то условие выбора любых двух вариантов из четырех возможных , запишется в виде:
х1+ х2+х3 +х4 =2
Если х1, х2,х3 , х4 булевы переменные то условие выбора по крайней мере одного вариантов , запишется в виде
х1+ х2+х3 +х4 =1
Если в исходной задаче неизвестная Х1= 9/2, то решая ее методом ветвей и границ, новые подзадачи образуются ограничениями:
а) первая подзадача будет содержать условия исходной задачи и дополнительное ограничение Х1 ≤ 4, а вторая подзадача образуется ограничением Х1 ≥ 5
Если задача ЦЛО решается методом ветвей и границ на максимум функции и в первой подзадаче f1max = 2500,25; а во второй f2max = 1900,75. Какую из подзадач при продолжении решения необходимо ветвить дальше?
первую
Задача ЦЛО решается методом ветвей и границ на максимум функции и в первой подзадаче f1max = 361,36; а во второй f2max = 450,93. Какую из подзадач при продолжении решения необходимо ветвить дальше?
первую
Задачи исследования операций в экономике это:
оптимизации цели системы при ограничениях на множество допустимых состояний системы
Задача линейной оптимизации называется вырожденной, если:
а) в столбце свободных членов симплексной таблицы имеется по крайней мере один нулевой элемент;
б) в столбце свободных членов симплексной таблицы все элементы положительные;
в) если в симплексной таблице имеются нулевые элементы.
3а разрешающий столбец при нахождении максимума целевой функции задачи линейной оптимизации выбирается тот:
а) в котором находится наименьший отрицательный элемент строки функции, за исключением элемента, находящегося в столбце свободных членов (ДА)
б) в котором находится отрицательный элемент строки функции;
в) в котором все элементы неотрицательные. НЕТ
Задача целочисленного линейного программирования переменные:
Принимают целые значения , ограниченные сверху
Задачи решаемые методом математического программирования являются:
а) любой класс задач
б) класс экстремальных задач
в) класс задач на экстремум (максимум или минимум) функции со многими неизвестными ДА
Задачей нелинейного программирования является задача, у которой:
а) нелинейной является целевая функция
б) некоторые или все ограничения являются нелинейными
в) функция и ограничения являются нелинейными
г) выполняется хотя бы одно из условий а, б или в
Задача линейного программирования на максимум решается графическим методом. Укажите точку, в которой целевая функция достигает своего максимального значения.
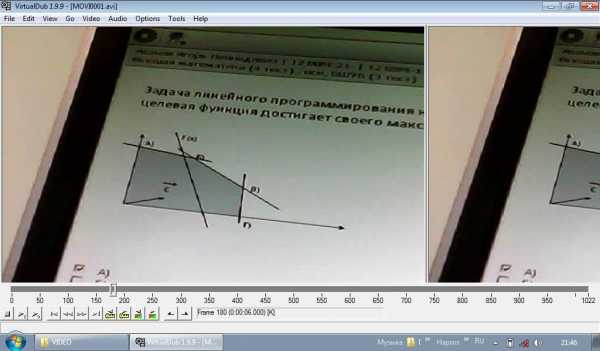
а) А (НЕТ)
б) Б ???
в) В
г) Г
Задача нелинейного программирования с ограничениями неравенствами может быть решена методом множителей Лагранжа если:
ограничения неравенства привести к равенствам и наложить условие неотрицательности на дополнительные переменные.
Задачу линейного программирования можно решить
а) Методом Лагранжа; б) графическим методом;в) методом наименьших квадратов;г) симплексным методом.
Задачу максимизации целевой функции Max Z=10Х1+2Х2-3Х3 можно заменить задачей минимизации целевой функции:
Z= -10Х1-2Х2+3Х3
Значение целевой функции в задаче Max Z=2x1+x2 при ограничениях х1-х2<=2 х1+3х2>=3 7х1-х2>=2 x1>=0, x2>=0 равно: ∞
Значения неизвестных системы линейных уравнений находятся:
а) по формуле Х= А-1 В, где А-1 – обратная матрица к матрице А из коэффициентов при неизвестных системы уравнений; В – вектор-столбец свободных членов
Запишите путь ………… длины между пунктами 1 и 9:
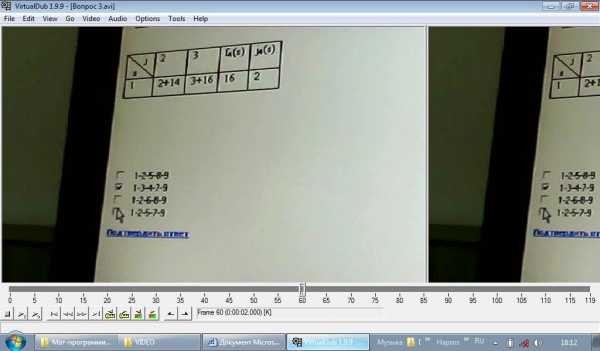
а) 1-2-5-8-9
б) 1-3-4-7-9 НЕТ
в) 1-2-6-8-9 НЕТ
г) 1-2-5-7-9
Какое программное средство можно использовать для нахождения ранга матриц, обратных матриц, решение систем линейных уравнений и оптимизационных задач?
Microsoft Exel
Какая функция Exel применяется для нахождения обратной матрицы?
Функция МОБР из диалогового окна Мастер функции
Какая функция Exel применяется для нахождения произведения матриц?
Математическая функция МУМНОЖ из диалогового окна Мастер функции
Какая команда Excel применяется для нахождения оптимального решения нелинейных задач?
Поиск решения из меню Сервис
Когда при решении задачи ЦЛО методом ветвей и границ на максимум функции заканчивается вычислительный процесс?
а) когда получено целочисленное решение
Каким (или какой) будет оптимальный план для задачи максимизации прибыли согласно даннной симплексной таблицы:
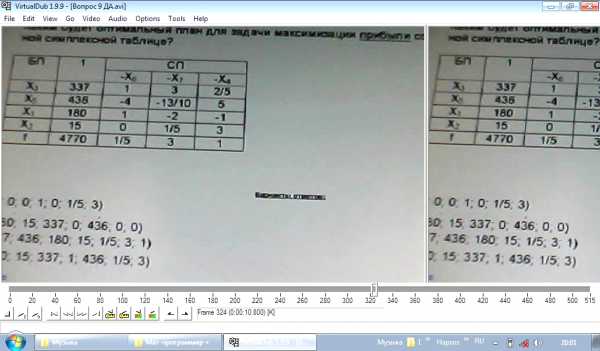
Ответ Б (ДА)
Каждой занятой клетке в таблице в транспортной задачи соответствует уравнение:
а) ui + vj < cp
б) ui + vj = cp ДА
в) ui + vj ≥ cp
г) ui ∙ vj = cp, где ui и vj - потенциалы
Какая команда Microsoft Excel используется для нахождения экстремума функции линейных задач математического программирования?
а) Поиск решения из меню Сервис;
б) Параметры из меню Сервис;
в) Любая команда из меню Сервис.
Какое из реккурентных соотношений для решения задачи фрмирования производственной программы по критерию минимизации затрат с учетом ограниченности производственных мощностей и складских площадей для хранения продукции является верным?
ответ Б
Какие из перечисленных элементов включает математическая модель задачи:
а) целевую функцию
б) теорему
в) систему ограничений
г) целевую функцию, систему ограничений, совокупность неизвестных (план задачи) х = (х1;……хn) ДА
д) доказательство
е) график
Какие методы относятся к методам нахождения начального опорного плана в транспортной задаче:
а) метод аппроксимации; б) метод минимального элемента;в) метод Лагранжа;г) метод Фогеля;д) метод «северо-западного угла».
Критерием оптимальности при нахождении минимума функции транспортной задачи служит:
а) неотрицательность значений потенциалов; б) неположительность оценок незаполненных клеток транспортной таблицы; в) неотрицательность оценок заполненных клеток транспортной таблицы; г) неотрицательность оценок незаполненных клеток транспортной таблицы.
Какое из утверждений верно:
а) каждой задаче линейной оптимизации можно поставить в соответствие задачу, называемую двойственной к исходной; (ДА)
б) для некоторых типов задач линейной оптимизации существует задача, называемая двойственной к исходной задаче;
в) каждой задаче линейной оптимизации можно поставить в соответствие несколько задач, двойственных к исходной.
Какое из утверждений верно:
а) если исходная задача является задачей максимизации целевой функции, то двойственная - задачей минимизации целевой функции;
б) если исходная задача является задачей максимизации целевой функции, то двойственная - также задача максимизации;
в) если исходная задача является задачей максимизации, то двойственная может быть как задачей минимизации, так и задачей максимизации.
Какое из утверждений верно?
а) потенциал i-го поставщика ui (i=1,m) является двойственной оценкой единицы запаса груза
этого поставщика.
б) потенциал j-го потребителя vj (j=1,n) является двойственной оценкой единицы запаса груза
этого поставщика.
Какое из утверждений верно?
а) двойственные оценки являются показателем дефицитности ресурсов и продукции;
б) двойственные оценки являются показателем влияния ограничений на значение функции;
в) двойственные оценки являются показателем эффективности производства отдельных видов продукции с позиций критерия оптимальности;
г) двойственные оценки являются инструментом сопоставления суммарных затрат и результатов;
д) верными являются все утверждения пунктов а), б), в) и г).
Какое из утверждений верно?
а) задача математического программирования — это задача на экстремум одного неизвестного;
б) задача математического программирования — это задача на экстремум функции многих переменных с ограничениями на область их изменения; ДА
в) задача математического программирования — это многовариантная задача, позволяющая найти какое-либо решение.
Какое из утверждений верно:
а) двойственные оценки являются инструментом сопоставления суммарных затрат и результатов.
б) верными являются все отверждения
в) двойственные оценки являются показателем дефицитности ресурсов и продукции.
в) двойственные оценки являются показателем влияния ограничений на значение функции.
г) двойственные оценки являются показателем эффективности производства отдельных видов продукции с позиции критерия оптимальности. ДА
Какое из утверждений верно?
а) динамическое программирование — математический метод для нахождения оптимальных решений многошаговых (многоэтапных) задач;
б) динамическое программирование — математический метод для нахождения всевозможных решений задач экономики, физики, биологии;
в) динамическое программирование — метод нахождения множества решений задачи управления во временном аспекте;
д) динамическое программирование — математический метод для нахождения решений дифференциальных уравнений.
Какое из рекуррентных соотношений для решения п-этапной задачи нахождения оптимального маршрута перевозки груза из города А в город В является верным, если S — состояние системы, a j — номер города?
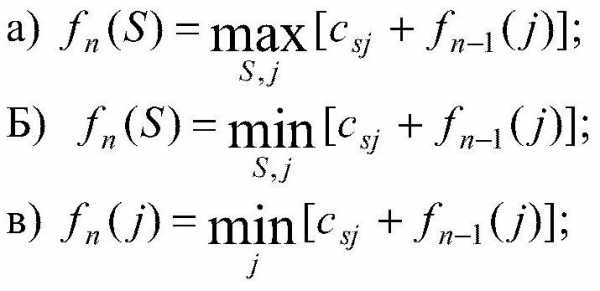
Ответ Б
Какое из записанных дополнительных ограничений построено верно по ограничении:
Ответ В
Какой командой вызывается диалоговое окно Параметры поиска решения?
а) Поиск решения;
б) Параметры диалогового окна Поиск решения;
в) Выполнить.
Ответ Б
Какие флажки необходимо установить в диалоговом окне Параметры поиска решения для решения линейной оптимизационной задачи?
а) Линейная модель;
б) Неотрицательные значения;
в) Флажки, указанные в пунктах а) и б).
Критерием оптимальности при нахождении минимума функции транспортной задачи служит:
а) неотрицательность характеристик Sij свободных клеток таблицы транспортной задачи;
б) неотрицательность оценок загруженных клеток таблицы транспортной задачи;
в) отрицательность оценок загруженных клеток;
г) равенство нулю потенциалов.
Критическим путем на сетевом графике проекта называется:
путь максимальной продолжительности
Какие дополнительные условия можно вводить при решении транспортной задачи?
а) запрет перевозки от i -го оставщика j-му потребителю;
б) фиксированную поставку груза;
в) нижнюю границу на поставку груза;
г) верхнюю границу на поставку груза;
д) все условия, перечисленные в пунктах а) — г) ДА
Коэффициенты целевой функции в двумерной задаче линейной оптимизации:
указывают направление движение к точке экстремума целевой функции
Математическая модель состояний экономической системы описывается:
ни каких ограничений на тип уравнений или неравенств не предусмотрено
Математическая модель транспортной задачи это:
задача линейного программирования
Математическая модель целевой функции экономической системы задается:
ни каких ограничений на вид целевой функции не предусмотрено
Математическая модель задачи линейной оптимизации может быть записана в следующей форме:
а) общей;
б) симметричной;
в) канонической;
г) Лагранжа;
д) числовой.
Математическая модель задачи линейной оптимизации записана в форме:
F = 8x1 +6x2 –3x3 (max)
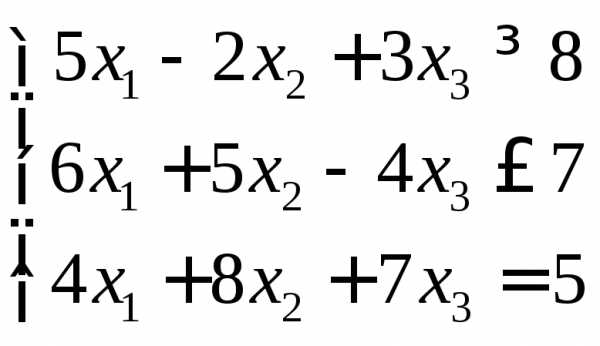
x1≥0, x2≥0, х3≥0.
1) симметричной;
канонической;
общей;
матричной.
Матрица строки и столбцы которой соответствуют вершинам графа, а элементы число ребер связывающих вершины называется матрицей:
Смежности
Модель двойственной задачи построенной к данной принимает следующий вид:
f = 8х1 - 4х2+ 7х3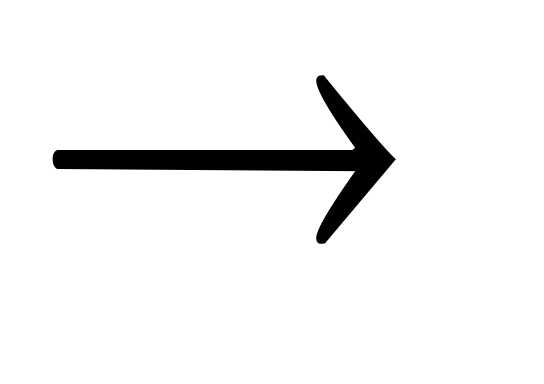 
max.
2х1+ 3х2 - 4х3
106,
5х1+ 4 х2 + х3 
205,
4х1+ 2х2+ 8х3 
340.
хj 
0, (j=
.
принимает следующий вид:
Матрица строки и столбцы которой соответствуют вершинам и ребрам графа, а элементы 1 или 0 в зависимости от наличия связи между вершинами и ребрами:
Инцидентностей
Метод Парето:
сокращает область поиска компромиссных решений многокритериальной оптимизации
Метод при котором для нахождения начального опорного плана записывается число в первую клетку:
а) метод Фогеля
б) метод северо-западного угла (ДА)
в) метод потенциалов
г) метод наименьшего элемента
Между переменными прямой и двойственной задачи можно:
а) установить взаимно однозначное соответствие;
б) произвести замену переменных;
в) установить регрессионную зависимость между переменными;
г) привести подобные члены.
Множители Лагранжа λi (i=1,m) показывают:
на сколько изменится значение функции в оптимальном решении при изменении правой части i-го ограничения на единицу:
Модель транспортной задачи это:
а) модель задачи линейной оптимизации;
б) модель сетевого планирования
в) модель динамического программирования или это.
Модифицированные жордановы исключения применяются для нахождения:
а) обратной матрицы;
б) ранга матрицы;
в) решений систем линейных уравнений;
г) решения задач оптимизации;
д) всего перечисленного в пунктах а), б), в) и г).
Начальный опорный план транспортной задачи ищется методом:
Северо-западного угла
Фогеля
Начальный опорный план транспортной задачи можно составить:
а) методом Жордана;
б) методом минимальной стоимости;
в) методом аппроксимации;
г) методом Фогеля;
д) применяя методы пунктов б) и г).
Найдите верные утверждения применительно к задаче рационального использования ограниченных ресурсов:
а) двойственные оценки в оптимальном решении задачи характеризуют дефицитность ресурсов;
б) ресурс, полностью использованный в оптимальном решении, является дефицитным, его двойственная оценка — больше нуля;
в) если ресурс расходован не полностью, то он избыточен, его двойственная оценка равна нулю;
г) если ресурс расходуется не полностью, то он избыточен, его двойственная оценка больше нуля.
На рисунке изображен случай, когда своего максимального значения функция f(х) достигает
|
Найдите правильное преобразование неравенства 11Х1 + 3Х2 > -19
-11Х1 – 3Х2 < 19
Область допустимых решений задачи линейной оптимизации:
а) может быть объединением двух выпуклых многоугольников НЕТ
б) может быть окружностью
в) может образовывать невыпуклый многоугольник с отрицательными координатами вершин.
г) может быть пустым множеством (ДА)
Область допустимых решений задачи линейной оптимизации:
а) может быть пустым множеством;
б) не может быть пустым множеством;
в) может быть точкой;
г) может быть отрезком прямой;
д) может быть окружностью;
е) может образовывать выпуклый многоугольник (в пространстве — многогранник).
Область допустимых решений задачи нелинейного программирования может быть:
а) выпуклой
б) вогнутой
в) из нескольких частей
г) выпуклой, вогнутой и состоять из нескольких частей
Основным принципом, на котором базируется оптимизация в задачах динамического программирования, является:
а) принцип оптимальности Р. Беллмана;
б) принцип особенностей вычислительного метода;
в) принцип планового соответствия переменных;
г) принцип дуализма.
Оценка свободной клетки ( 2; 1) равна
|
| ||||||||||||||||||||||||||||||||||||
studfiles.net
Расчётно-пояснительная записка
Министерство образования и науки Республики Белоруссии
Белорусский государственный университет информатики и радиоэлектроники
Факультет информационных технологий и управления
Кафедра «Автоматизированные системы обработки информации»
к курсовой работе
по курсу «Системный анализ и исследование операций»
на тему «Решение задач оптимизации линейного программирования»
Выполнил студент гр. 120603 _________ Пашкевич М. А.
Руководитель _________ ________________
Минск
2003 Г. Содержание
Содержание ……………………………………………………………………... 2
Введение ………………………………………………………………………… 3
1. Постановка задачи оптимизации …………………………………………… 7
2. Построение аналитической модели …………………………………………. 8
3. Обоснование и описание вычислительной процедуры …………………… 10
3.1. Обоснование вычислительной процедуры ………………………………. 10
3.2. Описание вычислительной процедуры ………………………………..… 10
4. Решение задачи оптимизации на основе симплекс-таблиц ………………. 12
4.1. Приведение аналитической модели к стандартной форме ……………... 12
4.2. Нахождение начального допустимого решения …………………...……. 14
4.3. Определение оптимального решения на основе симплекс-таблиц ….… 15
5. Анализ решения на чувствительность ………………………………….….. 21
6. Проверка оптимального решения в среде Microsoft Excel …………..…… 25
Заключение …………………………………………….……………………….. 27
Литература …………………………………………….……………………….. 28
Приложение 1. Протокол решения задачи оптимизации с использованием пакета SIMPLEX-M ……………………………………………………………. 29
Приложение 2. Рабочий лист Microsoft Excel с результатами решения задачи оптимизации ………………………………….………………………………… 31
Введение
Для решения задач оптимизации линейного программирования в наше время существует множество различных методов. Каждый человек время от времени оказывается в ситуации, когда достижение некоторого результата может быть осуществлено не единственным способом. В таких случаях приходится отыскивать наилучший способ. Однако в различных ситуациях наилучшими могут быть совершенно разные решения. Выбор зависит от сложности решаемой задачи. А ведь именно выбор метода оптимизации является одним их важнейших ее этапов. Наиболее перспективными в своем применении и развитии являются следующие группы методов:
– методы случайного поиска
– аналитические методы
– методы математического программирования.
Методы случайного поиска. На данный момент эти методы являются одними из самых перспективных в своем развитии. Методами случайного поиска решается практически любая задача. Основной идеей этих методов является поиск оптимума целевой функции или направлении к нему, путем перебора случайных совокупностей значений независимых переменных. При использовании данных методов в допустимой области изменения выбирается точка, в которой вычисляется значение целевой функции. Аналогичным образом выбирается еще одна точка, в которой так же вычисляется значении целевой функции. Это значение сравнивается с предыдущим, если новое значение целевой функции меньше исходного (в случае минимизации целевой функции), то новое значение запоминается вместе с координатами точки. Дальше продолжается выборка случайных точек и сравнение значений целевой функции в этих точка с ранее найденным значением. В основном количество точек задает тот, кто решает данную задачу. Но чем больше точек мы возьмем, тем точнее мы получим решение. Но количество точек ограничено так, как это связанно с громоздкими вычислениями. Методы случайного поиска реализуются с помощью ЭВМ.
Аналитические методы. Эти методы применяются в тех случаях, когда целевая функция имеет аналитическое выражение, дифференцируемое во всей области исследования, а число переменных невелико. При решении задач оптимизации нужно учитывать множество различных факторов, а это, как известно, влечет к увеличению числа переменных. И поэтому, число задач решаемых аналитическими методами ограничено.
Методы математического программирования. В эту группу методов входят:
- линейное программирование
- нелинейное программировании
- динамическое программирование.
Линейное программирование – один из первых и наиболее подробно изученных разделов математического программирования. Именно линейное программирование явилось тем разделом, с которого начала развиваться сама дисциплина «математическое программирование». Линейное программирование предназначено для решения задач оптимизации с линейными ограничениями на область изменения переменных. Подобные задачи решаются итерационными способами. Методы линейного программирования используются при оптимальном планировании производства при ограниченном количестве ресурсов, а так же для решения транспортных задач, задач о назначениях и др.
С изобретением и распространением ЭВМ, а так же с формулировкой, американским математиком Дж. Данцингом, симплекс-метода, теория и алгоритмический аппарат линейного программирования получила значительный толчок в развитии. Симплекс-метод является универсальным методом для решения любых задач линейного программирования, в отличие от нелинейного и динамического программирования, где нет универсального метода решения задач.
В настоящее время для решения задач оптимизации линейное программирование является одним из наиболее употребительных аппаратов математической теории оптимального принятия решения. Для решения задач линейного программирования разработано сложное программное обеспечение, дающее возможность эффективно и надёжно решать практические задачи больших объёмов. Эти программы и системы снабжены развитыми системами подготовки исходных данных, средствами их анализа и представления полученных результатов. В тоже время широкое распространение получили градиентные методы решения задач оптимизации. Эти методы используются в программе Microsoft Excel в надстройке «Поиск решения».
Нелинейное программирование – эта группа объединила в себе различные способы решения задач оптимизации, такие как градиентные, безградиентные и многие другие.
Объединяет эти методы то, что они используются в тех задачах, у которых нелинейная целевая функция или ограничения. В большинстве случаев это многошаговые методы. Еще их можно назвать методами последующего улучшения исходного решения. Чаще всего в таких задачах нельзя предугадать количество шагов, гарантирующих оптимальное решение. И кроме того от выбора величина шага зависит эффективность применения того или иного метода. Выбор метода решения задач нелинейного программирования определяется сложностью решаемой задачи. Стремление найти оптимальное решение за наименьшее количество шагов объясняет огромное количество методов нелинейного программирования. Из-за громоздкости и сложности реализации вычислений эти методы называют машинно-ориентированными или численными методами.
Динамическое программирование – это эффективный метод решения задач оптимизации многостадийных процессов или задач сводящихся к ним. Основателем является Р. Беллман. Решаемая задача разбивается на этапы – маленькие подзадачи. Решение начинается с последнего этапа и решается поэтапно. На каждом этапе должен учитываться принцип оптимальности Р. Беллмана: решение на каждом шаге выбирается таким образом, чтобы обеспечить эффективность на данном шаге и на всех последующих шагах. Таким образом, динамическое программирование определяет оптимальное решение n-мерной задачи путём её разбиения на N этапов, каждый из которых представляет подзадачу относительно одной переменной. Вычислительное преимущество такого подхода состоит в том, что мы занимаемся решением одномерных оптимизационных задач вместо большой n-мерной задачи.
Нет универсального метода для решения задач оптимизации, выбор его зависит от сложности задачи, вида математической модели (вид ограничений и целевой функции), требований к точности решения и других факторов.
studfiles.net
Математическая экономика - Стр 3
ное требование, как правило, обусловлено физической неделимостью объектов, характеризуемых этими переменными.
В рассмотренных задачах был задан или выбран один показатель, оценивающий качество (эффективность) системы или решения. Такие задачи называют однокритериальными. Существует немало прикладных задач, в которых было бы желательно добиться экстремального значения двух или более показателей, например, получить наибольшую прибыль при наименьших затратах ресурсов. Такие задачи называютмногокрите-
риальными или задачами векторной оптимизации. Довольно часто их сводят к однокритериальным задачам, выбрав один критерий в качестве оптимального (например прибыль), а на остальные показатели накладывают ограничения – «не более чем…» или «не менее чем…». Однако существуют и специальные подходы к анализу задач векторной оптимизации (см. например [27]).
До сих пор нами предполагалось, что все исходные данные, фигурирующие в задаче, например, нормы расхода материалов, удельная доходность от реализации продукции и т.д., однозначно определены и известны. Эти задачи называют детерминированными. Однако на практике такие ситуации встречаются далеко не всегда. Зачастую в формулировке задачи подобной четкой определенности нет. Многие исходные условия оказываются неопределенными, например, спрос на продукцию, которая запланирована к выпуску. Такие задачи называютсязадачами с неопределенностями. При их формализации и анализе используют специальные подходы, в частностивероятностно-статистические,интервальные и нечеткие модели [9, 11, 18].
В заключение отметим, что в теории оптимизации отсутствует ка- кой-либоуниверсальный метод, позволяющий одинаково эффективно решать различные типы оптимизационных задач. Развитие этой теории идет по пути разработки алгоритмов, обеспечивающих достаточно эффективное решение определенного класса задач, например, задач линейного программирования. Поэтому при решении конкретной оптимизационной задачи важно, прежде всего, правильно формализовать эту задачу и определить ее тип, что позволит далее перейти к выбору соответствующего алгоритма решения.
Контрольные вопросы
1.Какие действия необходимо осуществить для перехода от содержательной постановки задачи к математической модели?
2.В чем состоит задача статической оптимизации, каковы особенности задач динамической оптимизации?
3.Что такое целевая функция, какую роль она играет в оптимизационной задаче?
4.Как формулируется задача безусловной оптимизации?
5.Как формулируется задача условной оптимизации?
6.Как формулируется задача математического программирования?
7.Какой смысл имеет термин «программирование» в теории оптимизации?
8.В чем состоит сущность задач векторной оптимизации?
9.Какими особенностями обладают детерминированные задачи оптимизации?
10.Какие подходы используются при формализации и анализе оптимизационных задач с неопределенностями?
Задачи для самостоятельного решения
Требуется формализовать приведенные ниже задачи и определить их
тип.
1.Найти размеры прямоугольника, имеющего заданный периметр и максимально возможную площадь.
2.Из всех треугольников данного периметра p найти тот, который имеет наибольшую площадь.
3.Из проволоки заданной длины l необходимо изготовить равносторонний треугольник и квадрат. Требуется найти такие размеры этих фигур, чтобы их суммарная площадь была максимальна.
4.Малое предприятие изготавливает два вида красок: для внутренних K1 и наружныхK2 работ. Продукция обоих видов поступает в опто-
вую продажу. Для производства этих красок используются два исходных продукта П1 иП2 , их максимально возможные суточные запасы со-
ставляют 6 и 8 т соответственно. Расходы продуктов П1 иП2 на из-
готовление 1 т соответствующих красок известны. Они приведены в табл. 1.2. Изучение рынка сбыта показало, что суточный спрос на краску K1 никогда не превышает спрос на краскуK2 более чем на 1 т. Кроме то-
го, спрос на K1 никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны: 3 тыс. у.е. дляK1 и 2 тыс. у.е. дляK2 . Какое количе-
ство краски каждого вида должно производить предприятие, чтобы доход от реализации обеих красок был наибольшим? (Решение аналогично примеру 3 из § 1.1, оно приведено в [32]).
|
|
| Т а б л и ц а 1.2 |
|
|
|
|
Исходные | Расход исходных продуктов, | Максимально | |
продукты | на изготовление 1 т краски | возможный запас, т | |
|
|
|
|
Виды | K1 | K2 |
|
продукции |
|
|
|
П1 | 1 | 2 | 6 |
П2 | 2 | 1 | 8 |
5. Производственная мощность цеха сборки некоторого изделия составляет 120 шт. типа P1 и 360 шт. типаP2 в смену. Технический контроль
может пропустить в сутки не более 200 изделий того и другого типа. Доход от реализации изделий P2 в 4 раза выше, чем от реализацииP1 . Опреде-
лить план выпуска изделий, при котором будет обеспечена наибольшая прибыль.
6. Предприятие выпускает две модели электронных блоков Б1 иБ2 ,
причем каждая модель производится на отдельной технологической линии. Первая линия может выпускать 60 изделий в сутки, вторая – 75. В производстве обеих моделей используются однотипные узлы, суточный запас которых ограничен – он не может превышать 1000 штук. Причем на один блок 1-ймодели расходуется 10 узлов указанного типа, а для2-ймодели – 8 узлов. Прибыль от реализации одного блока1-ймодели равна 30 у.е., а второй – 20 у.е. Определить оптимальные суточные объемы производства.
7. Фирма имеет возможность рекламировать свою продукцию через радио- и телевизионную сеть. Для этих целей из бюджета фирмы выделяется 1000 у.е. в месяц. Каждая минута радиорекламы стоит 5 у.е., а телерекламы – 100 у.е. Опыт показывает, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого
23
одной минутой радиорекламы. Определить оптимальное распределение средств между радио- и телерекламой.
8. На предприятии изготавливаются изделия двух видов. Процесс изготовления каждого из них осуществляется последовательно в трех цехах. Время обработки и прибыль от продажи одного изделия каждого вида приведены в табл. 1.3. Рабочее время составляет 8 ч в сутки. Найти оптимальные объемы производства изделий каждого вида.
|
|
|
| Т а б л и ц а 1.3 |
|
|
|
|
|
Тип | Время обработки одного изделия, мин | Удельная прибыль, у.е. | ||
|
|
| ||
изделия | в цехе № 1 | в цехе № 2 | в цехе № 3 | |
|
|
|
| |
|
|
|
|
|
1-й | 10 | 6 | 8 | 2 |
2-й | 5 | 20 | 15 | 3 |
9. Формализовать задачу об оптимальном составе смеси. В ней требуется определить такие концентрации веществ в смеси, чтобы стоимость смеси была минимальна, а показатели, оценивающие ее свойства (плотность, прочность, теплоемкость и т.п.), были не меньше заданных значений. Примером такой задачи может служить задача об оптимальной диете (рационе). При откормке животных каждое из них ежедневно должно получить не менее 60 ед. питательного вещества А, не менее 50 ед. вещества В и не менее 12 ед. веществаС. Использоваться могут три вида корма. Содержание питательных веществ в каждом из них задается в табл. 1.4.
Составить дневной рацион, обеспечивающий получение необходимого количества питательных веществ при минимальных денежных затратах, если цена кормов 1-го,2-гои3-говидов составляет соответственно 9, 12 и 10 у.е.
|
|
| Т а б л и ц а 1.4 |
|
|
|
|
Питательные | Количество питательных веществ в 1 кг корма | ||
вещества | |||
|
|
|
|
| 1-говида | 2-говида | 3-говида |
А | 1 | 3 | 4 |
В | 2 | 4 | 2 |
С | 1 | 4 | 3 |
10. Для производства чугунного литья используется n различных исходных шихтовых материалов (чугун различных марок, стальной лом,
феррофосфор и др.). Химический состав чугунного литья определяется содержанием в нем химических элементов (кремния, марганца, фосфора и др.). Готовый чугун должен иметь строго определенный химический состав, который задается величинами H j , представляющими собой доли (%)
j-гохимического элемента в готовом продукте. При этом известны величины:hij – содержание (%)j-гохимического элемента вi-мисходном
шихтовом материале; ci – цена единицы каждогоi-гошихтового материала. Определить состав шихты, обеспечивающей получение литья заданного качества при минимальной общей стоимости используемых шихтовых материалов.
11. Имеются заготовки в виде листов материала определенного размера. Из них нужно накроить детали четырех видов: А – 6 шт., Б – 15 шт., В – 25 шт., Г – 10 шт. Известны три способа раскроя заготовки. Количество деталей каждого вида, получаемых при этих способах раскроя, приведено в табл. 1.5.
|
|
|
|
| Т а б л и ц а 1.5 | |
|
|
|
|
|
| |
Способ |
| Количество получаемых деталей из одной заготовки | ||||
раскроя |
|
|
|
|
|
|
А |
| Б | В |
| Г | |
1-й | 3 |
| 2 | 1 |
| 1 |
2-й | 2 |
| 4 | 1 |
| 2 |
3-й | 2 |
| 1 | 1 |
| 4 |
Найти оптимальный план раскроя заготовки, т.е. количество заготовок, при котором должно быть получено заданное количество деталей каждого вида из минимального количества заготовок.
12. Имеется n = 2 предприятийА1иА2 , в которых производится однородная продукция. Количество ежедневно производимой продукции в
каждом из них задано: а1 = 120 и | а2 | = 90. Эту продукцию нужно дос- |
тавить в m = 4 пунктов потребления: | B1,B2,B3 иB4 . Их ежедневные | |
объемы потребления заданы: в1 = 40, | в2 = 20,в3 =80 ,в4 = 70. Требуется | |
найти оптимальный план перевозок, определяющий количество продукции, перевозимой из пункта Аi в пунктB j (i = 1,2;j = 1,..., 4). Этот план
должен обеспечивать минимальные общие затраты на перевозки. При
этом стоимость cij | перевозки единицы продукции из пункта Аi | в пункт B j | ||||
задается табл. 1.6. |
|
|
|
|
| |
|
|
|
| Т а б л и ц а 1.6 | ||
|
|
|
|
|
|
|
B j |
| B1 | B2 | B3 |
| B4 |
Аi |
|
|
|
|
|
|
A1 |
| 2,3 | 4,7 | 1,8 |
| 1,1 |
A2 |
| 3,7 | 4,6 | 8,2 |
| 12,3 |
Примечание. В рассматриваемой задаче объем производства равен
объему потребления∑ai= ∑вj, т.е. система «производство – потребле- i j
ние» сбалансирована. В противном случае продукция либо «затоварилась» бы в пунктах потребления, либо возникал дефицит в ней.
Пусть xij – количество единиц продукции, перевозимой изАi вB j .
Тогда подлежащая минимизации общая стоимость перевозок будет определяться выражением
2 4
y = ∑∑cijxij, i=1 j=1
где cij – стоимости из табл. 1.6.
y = 2,3x11 + 4,7x12 +1,8x13 +1,1x14 +3,7x21 + 4,6x22 +8,2x23 +12,3x24. (1.12)
План должен быть составлен так, чтобы обеспечивался полный вывоз продукции из каждого пункта Аi и обеспечивалось полное удовлетворение спроса в каждом пункте потребленияBj . Это приводит к следую-
| 4 |
| 2 |
|
| |
щим двум группам условий: i : ∑xij = ai ; j :∑xij =b j : |
|
| ||||
| j=1 |
| i=1 |
|
| |
x11+ x12+ x13+ x14=120, | x11+ x21 | = 40, | x13+ x23 | =80, | (1.13) | |
x21+ x22+ x23+ x24= 90;} | x12+ x22 | = 20;} | x14+ x24= 70.} | |||
| ||||||
Таким образом, данная задача сводится к отысканию nm переменныхxi j ≥0, при которых выполняется система изn+m ограничений-равенств
(1.13), а целевая функция (1.12) принимает наименьшее значение. Эта задача является задачей линейного программирования, причем она имеет существенную особенность: все переменные xi j входят в ограничения-
равенства с единичными коэффициентами. Заметим, что в отличие от предыдущих задач при формализации рассмотренной транспортной задачи оказалось удобным использовать обозначение искомых величин в виде переменных с двойной индексацией, хотя можно было использовать и одноиндексные переменные xk (k =1,...,nm) .
13. Задача о назначениях (о распределении работ). В цехе имеется два участка А1 иА2 по контролю и настройке производимой электронной аппаратуры четырех разновидностей:B1,...,B4 . Известно, что оборудование участков и квалификация работающих там специалистов таковы, что на участке Аi на наладку одного изделия вида Bj требуется время Cij (ч)
(табл. 1.7).
|
|
|
| Т а б л и ц а 1.7 |
|
|
|
|
|
B j | B1 | B2 | B3 | B4 |
Аi |
|
|
|
|
A1 | 0,8 | 1,2 | 0,7 | 0,5 |
A2 | 0,9 | 1,0 | 0,8 | 0,4 |
Поступило задание: провести настройку 7 изделий вида B1 , 10 изделий –B2 , 14 изделий –B3 и 9 изделий –B4 . Как распределить эти изделия по участкам, чтобы общие затраты времени на их настройку были минимальными?
Глава 2. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
§ 2.1. Общая и каноническая задачи линейного программирования
Как указывалось в § 1.2, оптимизационную задачу называют задачей линейного программирования (ЛП), если она состоит в отыскании значений переменных x1,...,xn , при которых целевая функция, являющаяся ли-
нейной формой этих переменных:
y = c1x1 +... + cn xn , | (2.1) |
принимает наименьшее (или наибольшее) значение и выполняется система линейных ограничений-равенств:
a | x +...+ a | x |
| =b, |
|
| |
11 1 | 1n | n |
| 1 |
| (2.2) | |
|
| ... |
|
|
|
| |
a | x +...+ a | x |
| =b |
|
| |
m1 1 | mn n | m |
| ||||
и система линейных ограничений-неравенств: |
|
|
| ||||
| d | x +...+ d | x ≥ e, |
| |||
| 11 1 | 1n |
| n | 1 | (2.3) | |
|
| ... |
|
|
|
| |
|
|
|
|
|
|
|
|
| dk1x1 +... + dknxn≥ ek. |
| |||||
Примечание 1. При формализации конкретной задачи среди ограни- | |||||||
чений-неравенствмогут встретиться неравенства вида |
| ||||||
di1x1 +... + dinxn |
| ≤ ei , |
| (2.4) | |||
но они легко сводятся к виду (2.3) умножением обеих частей неравенства на (–1).
Примечание 2. Из физического смысла переменных, фигурирующих в задаче, довольно часто следует, что все либо часть этих переменных должны быть неотрицательны (см. пример 3 из § 1.1). Это приводит к по-
явлению особой группы условий: |
|
xi ≥ 0,i =1,...,p , | (2.5) |
хотя ясно, что они непосредственно вписываются в систему ограничений
(2.3).
Выделим частный случай сформулированной общей задачи ЛП, в которой находятся наименьшее значение линейной целевой функции (2.1) при выполнении системы ограничений-равенств(2.2) и требования неотрицательности всех переменных. Такая задача называется канонической задачей линейного программирования (КЗЛП) [1, 26], или основной (ОЗЛП) [6, 26], или стандартной [32].
Отметим, что с помощью матриц |
|
|
|
|
|
|
|
|
|
|
| ||||||||
|
| x |
|
| a | … a |
|
|
|
| b |
|
|
|
| c |
| ||
|
| 1 |
|
|
| 11 |
| 1n |
|
|
|
| 1 |
|
|
|
| 1 |
|
|
| ; |
|
|
| ; |
| ; |
| ||||||||||
| x = ... |
| A = |
| b = ... |
| c = ... |
| |||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| xn |
|
| am1 |
| amn |
|
|
| bm |
|
|
| cn |
| |||
соотношения (2.1), (2.2) и (2.5) записываются в краткой форме: |
| |||||
y = cT х; Ax | = |
| ; |
| ≥ 0. | (2.6) |
b | x | |||||
(Последнее условие означает, что все компоненты столбца х | должны | |||||
быть неотрицательны).
Общая задача ЛП отличается от канонической тем, что в ней может находиться как наименьшее, так и наибольшее значение целевой функции, а среди ограничений-неравенствкроме простейших условийxi ≥ 0 могут
присутствовать неравенства, в которые входят несколько переменных, например, 2x1 + x2 − x3 + 4x5 ≥10. В теории ЛП рассматривается главным
образом более простая КЗЛП. При этом учитывается то, что общую задачу ЛП всегда можно свести к канонической.
Если необходимо найти наибольшее значение целевой функции y, то для сведения этой задачи к канонической следует перейти к вспомогатель-
ной функции y = −y . Ясно, что при этом наименьшему значению~y будет
соответствовать наибольшее значение y и наоборот.
Допустим, что при формализации конкретной практической задачи
возникло ограничение-неравенство: |
|
ai1x1 +... + ainxn≥ bi. | (2.7) |
Введем новую дополнительную переменную xn+1, полагая: |
|
xn+1 = ai1x1 +... + ain x−bi . | (2.8) |
Тогда неравенству (2.7) будут эквивалентны два условия: |
|
ai1x1 +... +ain x −xn+1 =bi ; xn+1 ≥0, | (2.9) |
соответствующие условиям канонической задачи.
Пример. Формализация задачи 14 о планировании производства из § 1.3 приводит к следующей задаче ЛП: найти неотрицательные значенияx1 иx2 , при которых целевая функция, выражающая прибыль предпри-
ятия от реализации продукции
будет наибольшей при наличии ограничений, выражаемых системой неравенств:
x1+ 2x2≤ 6; | x1− x2 | ≤1; | (2.11) | |
2x1+ x2≤8; | x1≤ | 2. | ||
|
Требуется свести эту задачу к КЗЛП.
Решение. Преобразуем каждое из неравенств системы (2.11) к виду
n |
|
|
|
|
∑aijx j−b j≥0. |
|
| (2.12) | |
j =1 |
|
|
|
|
В результате получаем: |
|
|
|
|
6 −x1 −2x2 ≥0; 1−x1 +x2 | ≥ 0; |
| (2.13) | |
8 −2x1 − x2 ≥ 0; | 2 −x1 ≥ | 0. |
| |
|
| |||
Вводим дополнительные переменные: |
|
|
| |
x3 =6 −x1 −2x2; x5 =1 −x1 | + x2 | ; | (2.14) | |
x4=8 − 2x1− x2; х6= 2 − x1. |
| |||
|
| |||
Преобразуя эту систему к стандартному виду (2.2), т.е. перенося все члены уравнений, содержащие переменные xi , в левую часть, а свободные
члены – в правую, вместо исходной системы неравенств (2.11) получаем систему уравнений
x1+ 2x2+ x3= 6; x1− x2+ x5 | =1; | ||
2x1+ x2+ x4=8; x1+ x6= 2 | (2.15) | ||
| |||
и требования xi ≥ 0,i = |
|
|
|
1,6. |
| ||
Вводя вспомогательную функцию |
| ||
|
| y = −3x1 −2x2, | (2.16) |
получаем вместо исходной задачи об отыскании наибольшего значения функции (2.10) при выполнении неравенств (2.11) каноническую задачу об отыскании наименьшего значения функции (2.16) при выполнении системы линейных алгебраических уравнений (2.15) и требовании неотрица-
тельности всех переменных xi (i =1,6).
Будем в дальнейшем рассматривать задачи ЛП в канонической форме, считая, что в том случае, когда исходная задача окажется сформулированной в общем виде, она указанным выше образом будет сведена в КЗЛП.
Отметим, что каждый набор переменных ( x1,...,xn ), удовлетворяющий системе ограничений (2.2) и требованию неотрицательностиxi ≥ 0 (i =1,...,n ), называется допустимым решением рассматриваемой задачи ЛП, а множество всех таких наборов называетсяобластью допустимых решений (ОДР). Ясно, что для осуществления решения задачи ЛП необходимо (хотя и не достаточно), чтобы ОДР не была пустым множеством, а для этого нужно прежде всего, чтобы система уравнений (2.2) была совместна. Для этого (в соответствии с теоремой Кронекера – Капелли [17]) не-
studfiles.net
Задание 1 «Линейная оптимизационная задача»
Краткие теоретические сведения
Ежедневно специалисты в области экономики и менеджмента сталкиваются с задачами оптимизации. Это и премирование штатного расписания, и расчет фонда заработной платы, и планирование рекламной кампании, и еще множество задач, решаемых с помощью методов оптимизации. Наиболее легкими и показательными являются задачи линейной оптимизации.
Линейное программирование – это раздел высшей математики, занимающийся разработкой методов поиска экстремальных значений линейной функции, на неизвестные которой наложены линейные ограничения.
Задачи линейного программирования относятся к задачам на условный экстремум функции. Однако для исследования линейной функции многих переменных на условный экстремум нельзя применить хорошо разработанные методы математического анализа.
Действительно, пусть необходимо исследовать на экстремум линейную функцию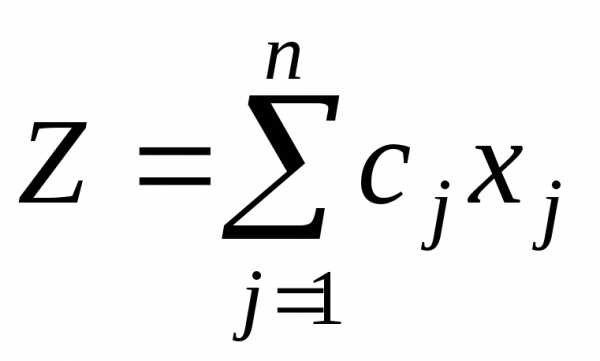 
при линейных ограничениях
(
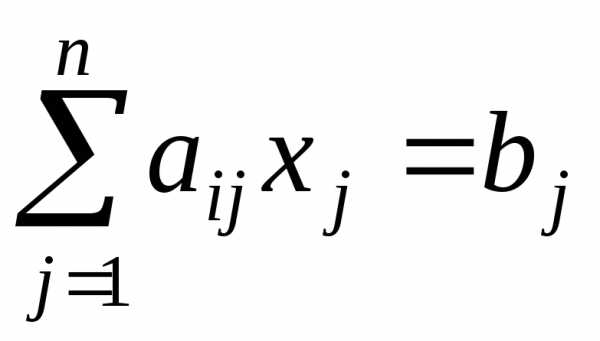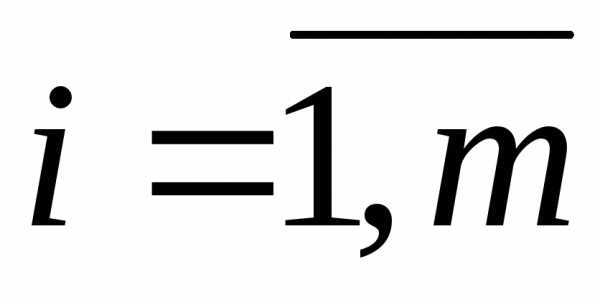). Необходимым условием экстремума является(
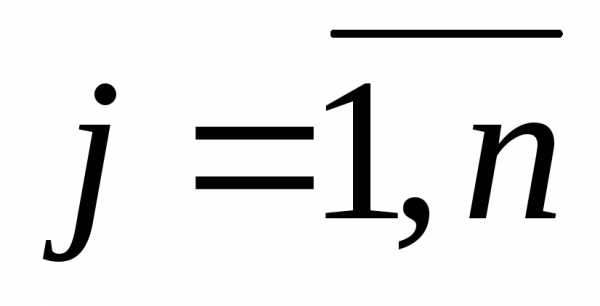). Но. Отсюда
(
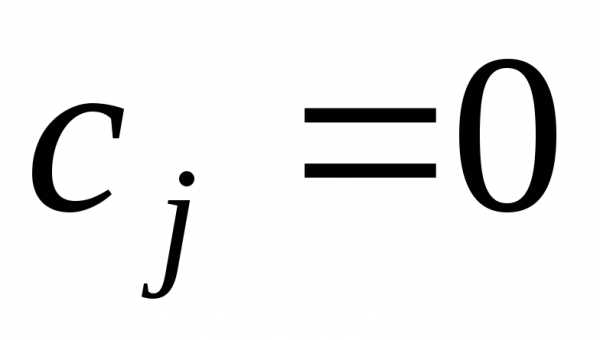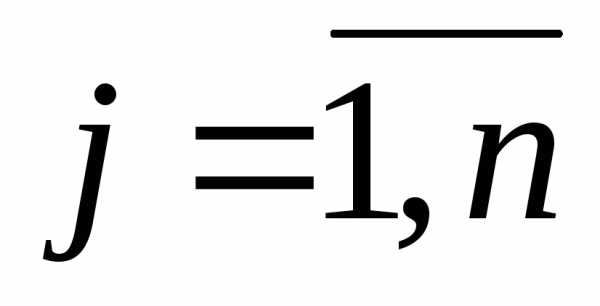). Так как все коэффициенты линейной функции не могут быть равны нулю, то внутри области, образованной системой ограничений, экстремальные точки не существуют. Они могут быть только на границе области.
Для решения таких задач разработаны специальные методы линейного программирования, которые особенно широко применяются в экономике.
Контрольный пример
Для производства столов и шкафов мебельная фабрика использует необходимые ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в следующей таблице:
Таблица 1
Нормы затрат ресурсов
| Нормы затрат ресурсов на одно изделие | Общее количество ресурсов | |
| стол | шкаф | ||
| Древесина: | |||
| 1 вида | 0,2 | 0,1 | 40 |
| 2 вида | 0,1 | 0,3 | 60 |
| Трудоемкость (человеко-часов) | 1,2 | 1,5 | 371,4 |
| Прибыль от реализации одного изделия (руб.) | 6 | 8 | |
Определить, сколько столов и шкафов фабрике следует изготовлять, чтобы прибыль от их реализации была максимальной.
Для решения этой задачи необходимо построить математическую модель. Процесс построения модели можно начать с ответа на следующие три вопроса:
Для определения каких величин строится модель?
В чем состоит цель, для достижения которой из множества всех допустимых значений переменных выбираются оптимальные?
Каким ограничениям должны удовлетворять неизвестные?
В данном случае мебельной фабрике необходимо спланировать объем производства столов и шкафов так, чтобы максимизировать прибыль. Поэтому переменными являются: х1 - количество столов, х2 - количество шкафов
Суммарная прибыль от производства столов и шкафов равна z=6*x1+8*x2. Целью фабрики является определение среди всех допустимых значений х1 и х2 таких, которые максимизируют суммарную прибыль, т.е. целевую функцию z
Ограничения, которые налагаются на х1их2:
объем производства шкафов и столов не может быть отрицательным, следовательно: х1, х2 0.
нормы затрат древесины на столы и шкафы не может превосходить максимально возможный запас данного исходного продукта, следовательно:
0.2x1+ 0.1x2 40
0.1x1 +0.3x2 60
Кроме того, ограничение на трудоемкость не превышает количества затрачиваемых ресурсов
1.2x1+ 1.5х2 371.4
Таким образом, математическая модель данной задачи имеет следующий вид:
Максимизировать
z = 6х1 + 8х2
при следующих ограничениях:
0.2x1+ 0.1x2 40
0.1x1 +0.3x2 60
1.2x1+ 1.5х2 371.4
Данная модель является линейной, т.к. целевая функция и ограничения линейно зависят от переменных.
Решение задачи с помощью MS Excel.
1. Отвести ячейки A3 и ВЗ под значения переменных х1 и х2 (рис. 1).
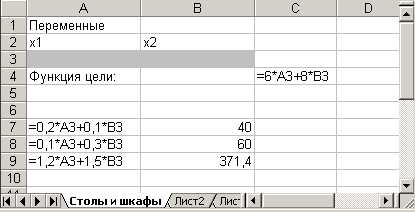
Рис. 1. Диапазоны, отведенные под переменные, целевую функцию и ограничения
2. В ячейку С4 ввести функцию цели: =6*АЗ+8*ВЗ, в ячейки А7:А9 ввести левые части ограничений:
=0,2*А3+0,1*ВЗ
=0,1*А3+0,3*ВЗ
= 1,2*АЗ+1,5*ВЗ,
а в ячейки В7:В9 - правые части ограничений. (рис.1).
3. Выбрать команды Сервис/Поиск решения и заполнить открывшееся диалоговое окно Поиск решения как показано на рис 2. Средство поиска решений является одной из надстроек Excel. Если в меню Сервис отсутствует команда Поиск решения, то для ее установки необходимо выполнить команду Сервис/ Надстройки/ Поиск решения.
Для ввода ограничений нажмите кнопку Добавить.
Внимание! В диалоговом окне Параметры поиска решения необходимо установить флажок Линейная модель (Рис.3.).
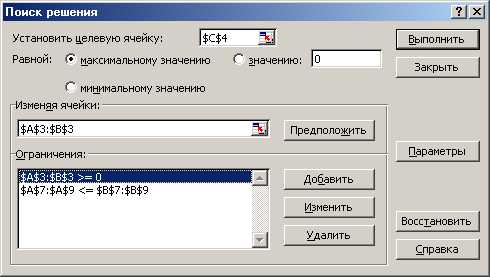
Рис. 2. Диалоговое окно Поиск решениязадачи о максимизации прибыли на фабрике
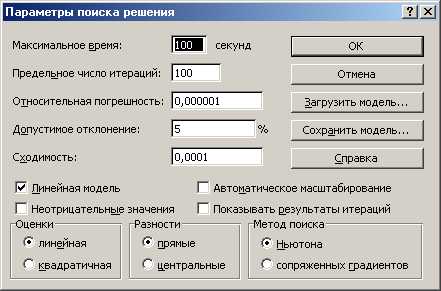
Рис 3. Параметры поиска решения
4. После нажатия кнопки Выполнить открывается окно Результаты поиска решения, которое сообщает, что решение найдено (рис. 4).
Рис. 4. Результаты поиска решения
5. Результаты расчета задачи представлены на рис. 5, из которого видно, что оптимальным является производство 102 столов и 166 шкафов Этот объем производства принесет фабрике 1940 руб. прибыли.
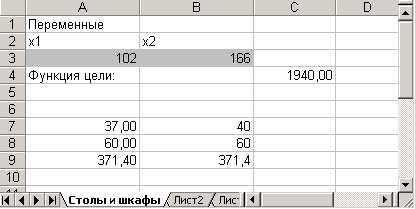
Рис. 5. Результаты расчета
Индивидуальное задание
Построить математическую модель задачи, согласно Вашемуварианту.
Решить задачу с помощью средства MSExсelПоиск решения.
studfiles.net
2. Общая задача оптимизации
Целью работы коммерческой фирмы является получение прибыли. Любое управленческое решение (будь то решение о количестве приобретаемого товара, или решение о назначении цены на реализуемый товар, или решение о подаче рекламы в газету и т.д.) будет влиять на прибыль в большую или меньшую сторону. Эти решения являются оптимизационными, то есть всегда существует возможность выбрать лучшее решение из нескольких возможных. Представим себе, что все управленческие решения принимаются наилучшим образом. То есть, все параметры, на которые может влиять фирма, являются оптимальными. Тогда фирма будет получать максимальную прибыль (больше получить при данных условиях невозможно). Для того чтобы определить, насколько управленческие решения, принимаемые работниками фирмы оптимальны, можно использовать методы математического программирования.
В экономике оптимизационные задачи возникают в связи с многочисленностью возможных вариантов функционирования конкретного экономического объекта, когда возникает ситуация выбора варианта, наилучшего по некоторому правилу, критерию, характеризуемому соответствующей целевой функцией (например, иметь минимум затрат, максимум продукции).
Оптимизационные модели отражают в математической форме смысл экономической задачи, и отличительной особенностью этих моделей является наличие условия нахождения оптимального решения (критерия оптимальности), которое записывается в виде функционала. Эти модели при определенных исходных данных задачи позволяют получить множество решений, удовлетворяющих условиям задачи, и обеспечивают выбор оптимального решения, отвечающего критерию оптимальности.
В общем виде математическая постановка задачи математического программирования состоит в определении наибольшего или наименьшего значения целевой функции f (х1, х2, ..., хn) при условиях gi(х1, х2, ..., хn) bi; (i =1,2,…m), где f и gi; – заданные функции, а bi – некоторые действительные числа. excel программирование графический симплексный
Задачи математического программирования делятся на задачи линейного и нелинейного программирования. Если все функции f и gi линейные, то соответствующая задача является задачей линейного программирования. Если же хотя бы одна из указанных функций нелинейная, то соответствующая задача является задачей нелинейного программирования.
В общем виде задача линейного программирования (ЗЛП) ставится следующим образом:
Найти вектор , максимизирующий линейную форму
(1)
и удовлетворяющий условиям
(2)
(3)
Линейная функция называется целевой функцией задачи. Условия (2) называются функциональными, а (3) – прямыми ограничениями задачи.
Вектор , компоненты которого удовлетворяют функциональным и прямым ограничениям задачи, будем называть планом, или допустимым решением ЗЛП.
Все допустимые решения образуют область определения задачи линейного программирования, или область допустимых решений. Допустимое решение, максимизирующее целевую функцию f(x), называется оптимальным планом задачи
,
где – оптимальное решение ЗЛП. Будем считать, что ЗЛП записана вканонической форме, если ее целевая функция максимизируется, ограничения имеют вид равенств с неотрицательной правой частью и все переменные неотрицательны.
На практике хорошо зарекомендовали себя следующие модели, относящиеся к оптимизационным: модели определения оптимальной производственной программы, модели оптимального смешивания компонентов, оптимального раскроя, оптимального размещения предприятий некоторой отрасли на определенной территории, модели формирования оптимального портфеля ценных бумаг, модели транспортной задачи.
studfiles.net
Решение ЗЛП
4. Оптимизационные экономико-математические модели
4.1. Общая задача оптимизации
В экономике оптимизационные задачи возникают в связи с многочисленностью возможных вариантов функционирования предприятия, когда возникают ситуации выбора варианта, наилучшего по некоторому правилу или критерию, характеризуемому соответствующей целевой функцией (например, иметь минимум затрат, максимум продукции).
Отличительной особенностью оптимизационных моделейявляется наличие условия нахождения оптимального решения (критерия оптимальности), которое записывается в виде функционала. Эти модели при определенных исходных данных задачи позволяют получить множество решений, удовлетворяющих условиям задачи, и обеспечивают выбор оптимального решения, отвечающего критерию оптимальности.
В общем виде математическая постановка задачи математического программированиясостоит в определении наибольшего или наименьшего значения целевой функциипри ограничениях
, где и- заданные функции,- некоторые заданные числа, а- переменные, определяемые экономическое содержание задачи.
Задачи математического программирования делятся на задачи линейного и нелинейного программирования.
Если все функции илинейные, то соответствующая задача являетсязадачей линейного программирования (ЗЛП), в противном случае перед намизадача нелинейного программирования (ЗНП).
В общем виде задача линейного программирования ставится следующим образом: найти вектор максимизирующий линейную форму
141Equation Chapter 1 Section 4242\* MERGEFORMAT (.)
и удовлетворяющий условиям
343\* MERGEFORMAT (.)
444\* MERGEFORMAT (.)
Линейная функция (4.1) называется целевой функцией задачи.
Условия (4.2) называют функциональными, а (4.3) – прямыми ограничениями задачи.
Вектор , компоненты которого удовлетворяют условиям (4.2 - 4.3), будем называть планом или допустимым решением ЗЛП.
Все допустимые решения образуют область определения ЗЛП, или область допустимых решений Допустимое решение, максимизирующие целевую функцию (1), называют оптимальным планом задачи
545\* MERGEFORMAT (.)
где - оптимальное решение ЗЛП.
На практике хорошо себя зарекомендовали оптимизационные модели определение:
оптимальной производственной программы;
оптимального смешения компонентов;
оптимального раскроя;
оптимального размещения предприятия некоторой отрасли на определенной территории;
формирования оптимального портфеля ценных бумаг;
транспортной задачи.
Для решения ЗЛП применяется метод последовательно улучшения плана, или симплекс-метод, который состоит из двух вычислительных процедур: симплекс-метода с естественным планом и симплекс-метода с искусственным планом (М-метод).
Выбор конкретной вычислительной процедуры осуществляется после приведения исходной задачи к каноническому виду (КЗЛП) [13]:
646\* MERGEFORMAT (.)
Будем считать, что ЗПЛ записана в канонической форме, если ее целевая функция максимизируется, ограничения имеют вид равенств с неотрицательной правой частью и все переменные не отрицательные.
4.2. Графический метод решения Задач линейного программирования (ЗЛП)
Графический метод решения ЗЛП является наиболее простым и применяется для решения задач ЛП с двумя переменными. Рассмотрим ЗЛП в стандартной форме (4.1)-(4.3). Положим , получим
(4.6)
при условиях
, (4.7)
Система неравенств (4.6) совместна (имеет хотя бы одно решение). Каждое неравенство этой системы графически определяет полуплоскость, ограниченную прямой
,
условия не отрицательности определяют полуплоскости с граничными прямыми (рис. 4.1).
Рис. 4.1. Схема построения ОДР и вектора-градиента
Система совместна, поэтому полуплоскости, как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством, координаты каждой точки которого удовлетворяют системе неравенств (4.7). Совокупность этих точек называют многоугольником решений. Он может быть точкой, отрезком, лучом, ограниченным и неограниченным многоугольником.
Таким образом, геометрически решение ЗЛП представляет собой отыскание такой точки многоугольника решений, координаты которой доставляют линейной функции цели.
Для нахождения экстремального значения целевой функции при графическом решении ЗЛП используют вектор-градиент, координаты которого, являются частными производными целевой функции:
747\* MERGEFORMAT (.)
Этот вектор показывает направление наискорейшего изменения целевой функции. Прямая , перпендикулярная вектору-градиенту, является линией уровня целевой функции.
В любой точке линии уровня целевая функция принимает одно и тоже значение. Приравниваем целевую функцию постоянной величине «a».Меняя значение«a»получим семейство параллельных прямых, каждая из которых является линией уровня целевой функции (ЦФ).
Важное свойство линии уровня ЦФ состоит в том, что при параллельном смещении линии в одну сторону уровень только возрастает, а при смещении в другую сторону уровень только убывает.
С геометрической точки зрения в ЗЛП ищется такая угловая точка или набор точек допустимого множества решений, на котором достигается самая верхняя (нижняя) линия уровня, расположенная дальше (ближе) остальных в направлении наискорейшего роста.
Графический метод решения ЗЛПсостоит из следующих этапов:
При минимизации (максимизации) функции линия уровня перемещается в направлении, противоположному вектору-градиенту. Если прямая, соответствующая линии уровня, при своем движении не покидает ОДР, то минимум (максимум) функциине существует.
Если линия уровня параллельна какому-либо ограничению задачи, то оптимальное значение ЦФ будет двигаться в любой точке этого ограничения, лежащей между двумя оптимальными угловыми точками, и соответственно, любая из этих точек является оптимальным решением задачи.
Возможные ситуации графического решения ЗЛП представлены в табл. 4.1.
Таблица 4.1
Возможные ситуации графического решения ЗЛП
| № | Вид ОДР | Вид оптимального решения |
| 1 | Ограниченная | Единственное решение |
| Бесконечное множество решений | ||
| 2 | Неограниченная | ЦФ не ограничена снизу |
| ЦФ не ограничена сверху | ||
| Единственное решение | ||
| Бесконечное множество решений | ||
| 3 | Отрезок | Единственное решение |
| Бесконечное множество решений |
Рассмотрим графическое решение задач линейного программирования на следующем примере.
Пример 4.1. Планирование выпуска продукции пошивочного предприятия.
Намечается выпуск костюмов двух видов – женских и мужских. На женский костюм требуется 1 м шерсти, 2 м лавсана и 1 чел./день трудозатрат. На мужской костюм – 3,5 м шерсти, 0,5 м лавсана и 1 чел./день трудозатрат. Всего имеется 350 м шерсти, 240 м лавсана и 150 чел./дней трудозатрат. Требуется определить, сколько костюмов каждого вида необходимо сшить, чтобы обеспечить максимальную прибыль, если прибыль от реализации женского костюма составляет 10 денежных единиц, а от мужского – 20 денежных единиц. При этом следует иметь в виду, что необходимо сшить не менее 60 мужских костюмов.
Экономико-математическая модель задачи
Введем обозначения: – число женских костюмов;– число мужских костюмов. Прибыль от реализации женских костюмов составляет, а от реализации мужских –, т.е. необходимо максимизировать целевую функцию:
.
Ограничения задачи имеют вид:
Первое ограничение по труду . Прямая проходит через точки и(рис. 4.2).
Второе ограничение по лавсану . Прямая проходит через точкии. Третье ограничение по шерсти, стоится аналогично. Добавим четвертое ограничение по количеству мужских костюмов. Решением этого неравенства является полуплоскость, лежащая выше прямой. На рис. 4.3 заштрихована область допустимых решений. Для определения направления движения к оптимуму построим вектор градиент, координаты которого являются частными производными целевой функции, т.е.
.
Чтобы построить такой вектор, нужно соединить точку с началом координат. При максимизации целевой функции необходимо двигаться в направлении вектора-градиента, а при минимизации – в противоположном направлении. Для удобства можно построить вектор, пропорциональный вектору-градиенту. Так, на рис. 4.4 изображен вектор-градиент.
Рис. 4.2. Решением первого неравенства является нижняя полуплоскость
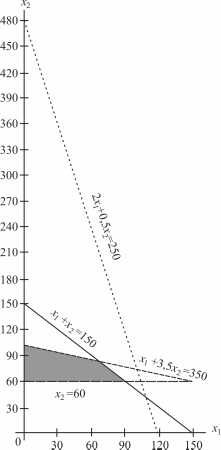
Рис. 4.3. Заштрихована область допустимых решений
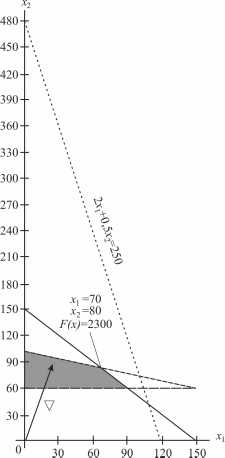
Рис. 4.4. Максимум целевой функции достигается в точке (70; 80)
В нашем случае движение линии уровня будем осуществлять до ее выхода из области допустимых решений. В крайней, угловой, точке достигается максимум целевой функции. Для нахождения координат этой точки достаточно решить систему из двух уравнений прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума:
Отсюда легко записать решение исходной ЗЛП: и достигается прии(рис. 4.4).
studfiles.net
