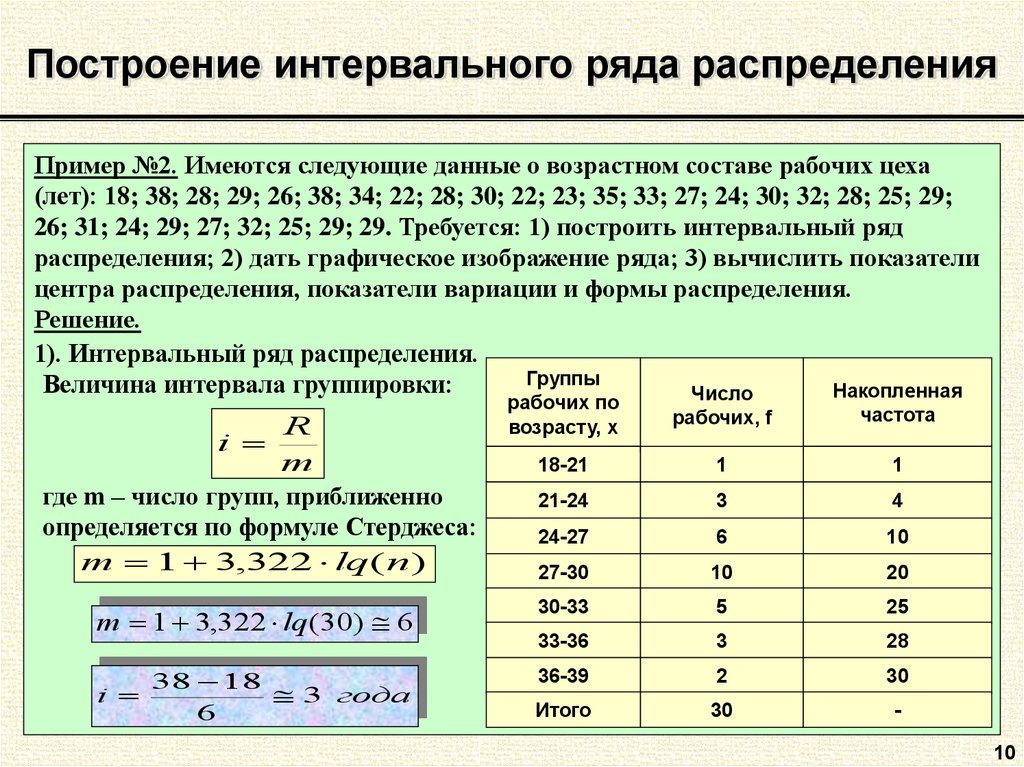
Содержание
Ранжирование выборки
Рассматривается ГС со случайным
признаком Х , измеренным в порядковой
шкале. Вариационный ряд выборки объёма
n из этой ГС в
идеальном случае имеет вид
(например, в случае непрерывной случайной
величины Х , когда вероятность
совпадения двух значений в выборке
равна 0). Но на практике в выборке могут
быть одинаковые значения, тогда
вариационный ряд имеет вид
.
Ранжированные выборки — это
приписывание каждому члену вариационного
ряда его порядкового номера – ранга в
вариационном ряду выборки.
Пример 1. Выборка 2, 5, 19, 8, 1, 4.
Вариационный ряд 1, 2 4, 5, 8, 19.
Ранги членов 1, 2, 3, 4, 5, 6.
Сложности в ранжировании возникают,
когда среди элементов выборки встречаются
совпадения, Тогда используют средние
ранги , которые могут быть дробными.
Пример 2.
Вариационный ряд 1 1 2 2 2
4 5 19,
Ранги членов 1,5 1,5 4 4 4
6 7 8,
так как 1,5 = (1 + 2) / 2 , 4 = (3 + 4 + 5) / 3.
При большом числе совпадающих значений
в выборке следует либо повысить точность
измерения признака Х , либо перейти
к номинативной шкале.
Проверка
гипотезы об однородности двух ГС по
критерию Уилкоксона (по критерию суммы
рангов)
Этот критерий эквивалентен критерию
Манна-Уитни.
Постановка задачи – как в критерии
Манна-Уитни.
Проверка гипотезы
по критерию Уилкоксона
Предварительная обработка выборок.
Записывается вариационный ряд для
выборок из ГС I и ГС II.
Затем общий вариационный ряд ранжируется.
Статистика критерия Уилкоксона
(статистика суммы рангов)
W(m,
n) = сумма рангов
элементов выборки из ГС I
в общем вариационном ряду. Аналогично
можно определить статистику W(n,
m).
Существует связь статистик Уилкоксона
и Манна-Уитни:
.
Поэтому применение критерия Уилкоксона
даёт тот же результат, что и критерий
Манна-Уитни.
3. По данному УЗ α при использовании
правостороннего критерия по таблицам
находят
.
Для левостороннего критерия
.
(*)
При двустороннем критерии по таблицам
находят
и по формуле (*) —
.
По выборкам находят выборочное значение
статистики критерия.
 Если
Еслипопадает в допустимую область, то
принимается. В противном случае
отвергается.
Постановка задачи. Пусть
выборка из ГС I ,
— выборка из ГС II и объёмы
выборок одинаковы равны n.
Считается, что выборки связаны парами
.
(*)
Пары независимы друг от друга, но
и
в парах связаны некоторым образом.
Гипотеза об однородности
:
законы распределения ГС I
и ГС II одинаковы.
Практически важная интерпретация
задачи.
На объекты ГС I оказывается
некоторое воздействие, которое может
оказать влияние на распределение
признака Х объектов ГС I.
После воздействия получаем ГС II.
Изменилось ли распределение признака
Х после воздействия или оно осталось
таким же, как было в ГС I
? Иными словами, произвело ли воздействие
наблюдаемый эффект на объекты ГС I
?
Гипотеза
— воздействие не имело эффекта.
Гипотеза
— проявился эффект воздействия.
Для проверки
из ГС I производят выбору
n объектов, у которых
измеряют величину Х до воздействия,
получая выборку
,
и, после воздействия, получая выборку
.
Отсутствие или наличие эффекта
воздействия, то есть гипотеза
, проверяется по парам (*).
Ранжирование сайтов по финансовой тематике в Google: исследование алгоритмов
12200 98 7
| SEO | – Читать 12 минут |
Прочитать позже
Вячеслав Вареня
Google Product Expert и автор канала
SEO inside
В свете последних Google Core Update-ов мы все чаще замечаем, что страдают сайты YMYL-страницы, а «наказывает» поисковик их за несоответствие параметрам E-A-T. Стало понятно, что нужно уделять больше внимания качеству контента, повышать авторитет и доверие к сайту. Но что же еще?
Я решил провести собственное исследование на примере финансово-кредитной тематики, чтобы понять, как Google классифицирует YMYL-сайты и какие показатели влияют на распределение страниц в топ-30.
Содержание
- Об исследовании
- Цель исследования
- Методология
- Ход исследования
Выводы
Disclaimer: все сформулированные выводы и выявленные закономерности основаны на данных моей выборки. Мои результаты могут отличаться от результатов других экспертов. Все написанное носит рекомендательный характер.
Об исследовании
В последние годы в лексикон вебмастера прочно вошли такие термины, как «E-A-T» и «YMYL».
Напоминаю, что YMYL — это страницы общественно значимых тематик, таких как новости, финансы, медицина, покупки и так далее.
Что касается E-A-T — это набор критериев для оценки качества страницы и расшифровывается эта аббревиатура как Экспертиза, Авторитет, Доверие (Надежность).
Меня эта тема очень интересует и недавно я опубликовал исследование «Как Google классифицирует YMYL сайты». Исследование было проведено на выборке интернет-страниц сайтов медицинской тематики.
Исследование было проведено на выборке интернет-страниц сайтов медицинской тематики.
Результаты оказались настолько интересными, что в комментариях и в социальных сетях меня начали просить провести такое же исследование для других тематик. Один из веб-мастеров даже список сайтов финансово-кредитной тематики прислал, за что ему огромное спасибо.
В этой статье я расскажу, как при помощи Serpstat и других SEO-инструментов я провел исследование YMYL-страниц финансово-кредитной тематики, чтобы определить, какие факторы влияют на их ранжирование.
Цель исследования
Изучение качественных характеристик интернет страниц и выявление общих закономерностей, которые могут быть присущи при продвижении сайтов финансово-кредитной тематики.
Методология
По 87 доменам финансово-кредитной тематики собраны запросы и страницы из топ-30 поисковой выдачи Google. При помощи интеллектуального анализа данных и машинного обучения были выявлены основные критерии (показатели), которые больше всего влияют при продвижении сайтов финансово-кредитной тематики. Первоначальная выборка составила 15013 страниц. После очистки и форматирования данных окончательный объем выборки составил 10830 интернет-страниц.
Первоначальная выборка составила 15013 страниц. После очистки и форматирования данных окончательный объем выборки составил 10830 интернет-страниц.
Теперь подробнее по шагам
Используя выборку из 87 доменов финансово-кредитной тематики, мы собрали список страниц этих доменов и ключевиков, по которым они ранжируются в топ-30 выдачи. Для каждого URL получили также позиции, показатели трафика и ключевые фразы. Чтобы собрать эти данные, мы использовали API-Консоль Serpstat.
Выбираем поисковую систему и регион. В нашем случае это Google Russia (при необходимости для поиска можно воспользоваться подсказкой сбоку).
Выбираем API метод. В нашем случае это Domain Keywords (да, выше мы писали, что собираем топ-30 URL и данные по ним, но чуть ниже вы поймете, почему именно этот метод).
В Queries вводим свой запрос. У нас — список из 87 доменов финансово-кредитной тематики.
В Position выставляем позиции от 1 до 30.
Загружаем данные (это может занять некоторое время, у меня ушло около 30 сек).
Получаем такую табличку, но это еще не все.
Переходим на вкладку SQL и выбираем «SQL Snippets→ Group by URL→ Value SQL».
Группировка данных таким образом позволит сэкономить API-лимиты. В конечном результате мы получаем такой список URL по доменам из топ-30 (15013 страниц).
Данные можно быстро выгрузить для более комфортной работы. Вот результат, который получчился у нас (пример 50 URL из 15К полученных).
Хотите узнать, как использовать API Serpstat для автоматизации
рутинных задач?
Заказывайте бесплатную персональную демонстрацию сервиса, и наши специалисты вам все расскажут! 😉
| Оставить заявку! |
| Узнать подробнее! |
Для анализа факторов ранжирования YMYL-сайтов собираем дополнительные параметры. При помощи Netpeak Spider по каждому URL были собраны On-Page показатели.
Используя интеграцию API Majestic и Netpeak Checker получены показатели метрик Majestic для домена и страницы.
Всего в наборе данных мы получили 41 параметр для анализа факторов ранжирования YMYL-страниц. Естественно, что такой объем данных невозможно проанализировать вручную. Поэтому без автоматизации процессов анализа тут не обойтись.
Вот несколько инструментов, которые будут полезны для таких задач:
Инструмент Answerminer использовался для определения корреляции между показателями набора данных.
Программное обеспечение Orange использовалось для интеллектуального анализа данных.
BigML для машинного обучения. Эти инструменты бесплатные.
Между настоящим и будущим: как искусственный интеллект меняет SEO
| Читать |
Ход исследования
Я загрузил свой набор данных в Orange. Планировал кластеризовать данные при помощи метода k-means и надеялся, что полученные кластеры дадут «пищу» для анализа. К сожалению, обучение данных без учителя (кластеризация), не дало мне той информации, на основе которой, можно сделать какие-то выводы.
Планировал кластеризовать данные при помощи метода k-means и надеялся, что полученные кластеры дадут «пищу» для анализа. К сожалению, обучение данных без учителя (кластеризация), не дало мне той информации, на основе которой, можно сделать какие-то выводы.
Учитывая это, я использовал другой подход. Классифицировал страницы в наборе данных, разделив их на три группы: топ-10, топ-20, топ-30.
Загрузив набор данных в Answerminer, я хотел выяснить, какой из показателей имеет самую высокую корреляцию с показателем «Позиция».
Оказалось, что показатель «Позиция» имеет сильную отрицательную корреляцию по Спирмену с показателем «Citation Flow — Majestic : Host».
При отрицательной корреляции низкие значения показателя «Позиция» соответствуют высоким значениям показателя «Citation Flow — Majestic: Host», что весьма логично.
Тут я сделаю две ремарки:
Во-первых, корреляция — это лишь сигнал о том, что между двумя признаками возможно существует причинно-следственная связь, но этой связи может и не быть.

Во-вторых, «Citation Flow — Majestic : Host» — одна из метрик потока Majestic, которая рассчитывается в соответствии с количеством веб-сайтов, ссылающихся на целевой URL (режим: Host).
В Orange я отсортировал показатели по релевантности. «Citation Flow — Majestic: Host» оказался вторым по релевантности в наборе данных после «Позиция».
Разница в средних значениях показателя «Citation Flow — Majestic: Host» между группами топ-10,топ-20, топ-30 статистически значима, т.е. не случайна. Среднее значение CF Majestic: Host для доменов финансово-кредитной тематики в топ-10 составляет 35, для топ-20 — 22, соответственно, а для топ-30 — всего 18.
Затем я загрузил мой набор данных в BigML, создал модель, обучил, оценил ее и выявил, что основным предиктором дерева решений (точка от которой начинают расходиться «ветки») также является показатель CF Majestic: Host.
В общем, для доменов финансово-кредитной тематики ссылки являются одним из определяющих факторов ранжирования.
Третьим по релевантности в наборе данных оказался показатель «Trust Flow — Majestic: Host».
Кстати, в модуле «Анализ ссылок» Serpstat есть схожая метрика — SDR (Serpstat Domain Rank). Принцип расчета показателя похож на Google Page Rank: числовой показатель зависит от того, сколько сайтов ссылаются на анализируемый домен + сколько сайтов ссылаются на сайты, ссылающиеся на анализируемый домен + сколько сайтов ссылаются на сайты, ссылающиеся на сайты, ссылающиеся на анализируемый домен — и так учитываются все сайты в индексе. Эту метрику можно получить и через API обратных ссылок.
Распределение страниц по показателю CF Majestic: Host в зависимости от позиции в поисковой выдаче.
На графике:
по горизонтали — значение позиции;
по вертикали — показатель метрики CF Majestic: Host;
размер элементов — показатель метрики TF — Majestic: Host.

Как видим, группа страниц из топ-10 имеет высокие показатели цитируемости (CF) и траста (TF).
Так что, не только количество ссылающихся доменов имеет значение, но и их качество. Что интересно, средний показатель TF — Majestic: Host для топ-10 составляет 27, что почти в два раза больше, чем у подгруппы топ-20 и топ-30.
Очень интересным мне показалось отличие между этими группами по показателю «Размер HTML» (количество символов в блоке <html>, включая HTML-теги). Сразу скажу, в моем наборе данных эти различия не статистически значимы (вероятно случайны).
На графике:
Распределение страниц по параметру «Размер HTML» в зависимости от позиции в поисковой выдаче.
На графике:
по горизонтали — показатели позиции;
по вертикали и в размере элементов — значение показателя «Размер HTML».

Как видно на графике, «Размер HTML» у многих YMYL-страниц финансово-кредитной тематики из топ-10 значительно больше, чему YMYL-страниц из топ-20/30.
Вернемся к нашему показателю CF Majestic: Host.
Обученная в BigML модель говорит о том, что если значение CF Majestic: Host больше 32, и ключевое слово не содержит слово «паспорту», ваш URL с 99,9% уровнем уверенности попадет в топ-10.
Чем хорошо машинное обучение, так это тем, что с его помощью можно рассмотреть несколько сценариев.
Модель дерева решений, созданная с использованием алгоритмов машинного обучения.
Почти с таким же высоким уровнем уверенности можно прогнозировать, что страница попадет в топ-10, если:
CF Majestic: Host будет меньше 32, но…
Title не будет содержать слово «РКО» (расчетно-кассовое обслуживание).
Длина Description от 101 до 205 символов.
Внутренних ссылок больше 90.

Количество слов в <p> меньше 2174.
Запрос не должен содержать слово «Паспорту».
Анализ тем страниц YMYL-страниц финансово-кредитной тематики.
Основной контекст страниц финансово-кредитной тематики соотносятся с названиями банковских отделений, адресами их отделений, режимом работы и тому подобное.
На графике видно, что одной из самых востребованных тематик также является «Займ, срочно».
Если кто-то забыл, напоминаю, что Google использует специальный алгоритм для тестирования подобных запросов на спам. Страницы с контекстом содержимого «Займ, срочно» изначально рассматриваются, как подозрительные.
Давайте сравним облако слов из Title, Description, h2 страниц из топ-10 и страниц из топ-30.
Сравнение «Облаков слов» страниц из топ-10 и топ-30.
Чем больше слово в облаке слов, тем чаще оно упоминается в Title, Description и h2.
Не знаю, как вам, но мне тематика страниц из топ-10 кажется более сбалансированной и менее спамной.
Также обратите внимание на то, что на страницах из топ-30, ключевые слова в Title, Description и h2 упоминаются чаще (их размер на Рис.4 больше), чем на страницах из топ-10.
В связи с этим, меня заинтересовал показатель «Конкуренция», который используется в Serpstat для целей PPC. Он показывается по шкале от 0 до 100%. Чем больше доменов использую данную фразу в объявлениях, тем выше конкуренция.
Давайте посмотрим на уровень конкуренции между нашими группами интернет-страниц.
Сравнение уровня конкуренции.
На графике мы видим, что показатель конкуренции для страниц из топ-10 меньше, чем для страниц из топ-20 и топ-30. Это подтверждается визуализацией на предыдущем графике.
Причем разница в уровне конкуренции между страницами из топ-10 и страницами из топ-20/30 статистически значима (неслучайна).
Экстраполируя определение показателя «Конкуренция» для страницы, можно предположить, что на страницах из топ-20/30 в моем наборе данных может быть «переспам» ключевыми словами в Title, Description и h2.
Обратите внимание, что мое допущение о показателе «Конкуренция» и «переспаме» — это предположение и вы просто примите это к сведению.
Выводы
Для этой тематики определяющим фактором является количество (CF Majestic >32) и качество (TF Majestic >28) реферальных (ссылающихся) доменов.
Страницы, в Title которых есть слово «РКО» и ключевой запрос на которых содержит слово «паспорту», сложнее попадают в топ-10.
Дальнейшее продвижение страниц из топ-20/30 в топ-10 может сдерживаться вероятным переспамом ключевых слов в Title, Dtscription и h2.
Страницы с количеством слов до 2200 имеют более высокие шансы пробиться в топ-10, чем страницы с большим количеством слов.
Чтобы быть в курсе всех новостей блога Serpstat, подписывайтесь рассылку.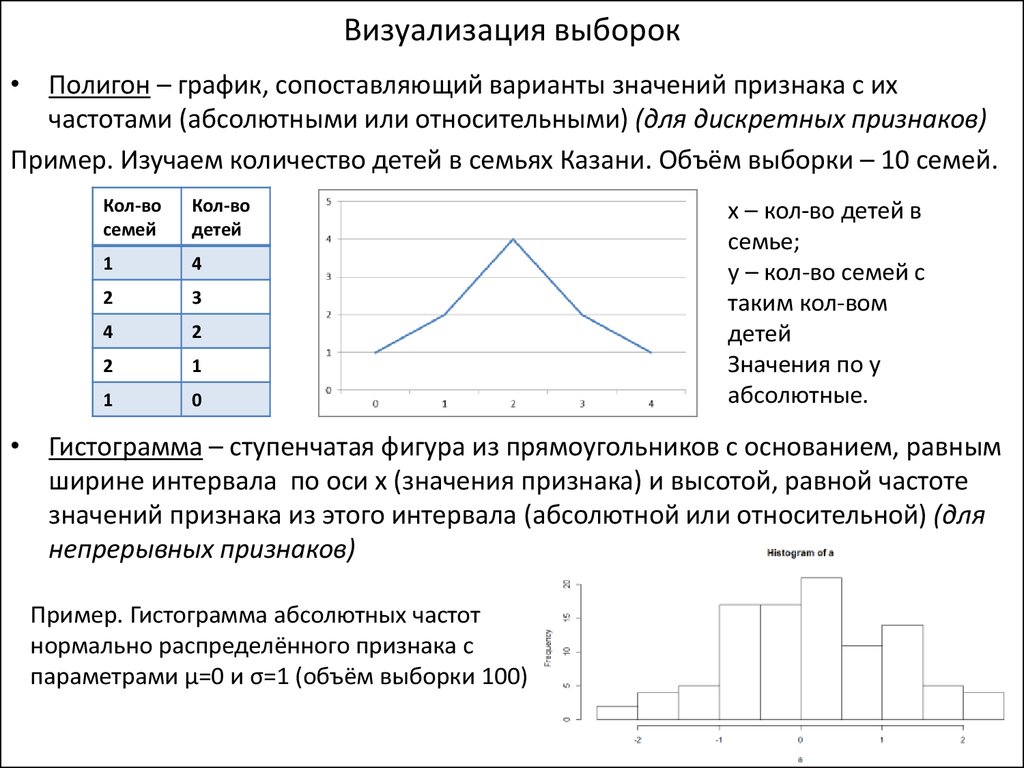 А также вступайте в чат любителей Серпстатить и подписывайтесь на наш канал в Telegram.
А также вступайте в чат любителей Серпстатить и подписывайтесь на наш канал в Telegram.
Serpstat — набор инструментов для поискового маркетинга!
Находите ключевые фразы и площадки для обратных ссылок, анализируйте SEO-стратегии конкурентов, ежедневно отслеживайте позиции в выдаче, исправляйте SEO-ошибки и управляйте SEO-командами.
Набор инструментов для экономии времени на выполнение SEO-задач.
Получить бесплатный доступ на 7 дней
Мнение авторов гостевого поста может не совпадать с позицией редакции и специалистов компании Serpstat.
Оцените статью по 5-бальной шкале
4.08 из 5 на основе 25 оценок
Нашли ошибку? Выделите её и нажмите Ctrl + Enter, чтобы сообщить нам.
Рекомендуемые статьи
SEO
Игорь Шулежко
«100 мобильных телефонов для манипуляций с выдачей» и еще куча SEO-инсайдов: интервью с Крейгом Кэмпбэллом
SEO +1
Владимир Товпеко
Как своими силами поднять блог с 0 до 38К трафика и заставить его продавать — кейс Fine shoes
SEO
Геннадий Федоров
Как увеличить скорость загрузки сайта?
Кейсы, лайфхаки, исследования и полезные статьи
Не успеваешь следить за новостями? Не беда! Наш любимый редактор подберет материалы, которые точно помогут в работе. Только полезные статьи, реальные кейсы и новости Serpstat раз в неделю. Присоединяйся к уютному комьюнити 🙂
Только полезные статьи, реальные кейсы и новости Serpstat раз в неделю. Присоединяйся к уютному комьюнити 🙂
Нажимая кнопку, ты соглашаешься с нашей политикой конфиденциальности.
Поделитесь статьей с вашими друзьями
Вы уверены?
Спасибо, мы сохранили ваши новые настройки рассылок.
Сообщить об ошибке
Отменить
Design Ranked Set Sampling
Design Ranked Set Sampling
Справочная информация
Ранжированная выборка набора, первоначально разработанная McIntyre
(1952), сочетает в себе простую случайную выборку с
профессиональные знания и суждения для выбора мест для сбора образцов.
В качестве альтернативы, полевые скрининговые измерения могут заменить профессиональное суждение.
когда это уместно. Использование ранжированной выборки увеличивает вероятность
что собранные образцы дадут репрезентативные измерения. Этот
приводит к более точной оценке среднего значения, а также к повышению производительности
многих статистических процедур, таких как проверка на соответствие
или базовые (справочные) стандарты.
Более того, ранжированная выборка может быть более рентабельной, чем простая выборка.
случайная выборка, поскольку требуется собрать и измерить меньше образцов.
Использование профессионального суждения в процессе выбора выборки
местоположений является мощным стимулом для использования ранжированной выборки. Профессиональный
суждение обычно применяется путем визуальной оценки некоторых характеристик
или особенность различных потенциальных мест отбора проб в поле, где
характеристика или особенность является хорошим индикатором относительной суммы
интересующей переменной или загрязняющего вещества, которое присутствует.
Простой экологический пример иллюстрирует выборку ранжированного множества
метод. Предположим, необходимо оценить средний возраст деревьев на участке.
Соответствующее измерение, основанное на суждениях (визуальный размер дерева —
деревья обычно увеличиваются в размерах с возрастом). Начать случайным образом
выбрать три дерева и определить на глаз, какое дерево самое маленькое. Отметка
Отметка
самое маленькое дерево, которое нужно измерить, и игнорировать два других. Далее случайным образом
выберите другой набор из трех деревьев для ранжирования. Отметьте дерево среднего размера
и игнорировать два других. Затем случайным образом выберите еще три дерева. Отметка
самое большое дерево и игнорировать два других. Повторите эту процедуру 10 раз
(10 циклов) всего 90 деревьев. 30 деревьев будут отмечены
и 60 игнорируются. Из 30 отмеченных деревьев 10 относятся к толще обычно
более мелкие деревья, 10 из пласта деревьев в целом среднего размера и
10 из пласта обычно более крупных деревьев. Определить возраст
каждое из 30 помеченных деревьев с помощью сердцевины или другого подходящего измерения
метод и использовать это измерение для оценки среднего возраста
деревья на участке.
На этом рисунке было выбрано 10 циклов и 3 выборки для каждого цикла.
На практике количество точек отбора проб, выбранных за цикл («множество
размер»), а количество циклов определяется с помощью систематического
Процесс планирования. Visual Sample Plan реализует систематический процесс
Visual Sample Plan реализует систематический процесс
необходимо определить количество циклов, а значит, и количество локаций
для ранжирования и количество местоположений для измерения. ВСП также может
нанести места ранжирования и отбора проб на карту исследуемого участка.
Реализация примера в виде сбалансированной (симметричной) схемы в VSP
В VSP начните с пустого проекта и нарисуйте прямоугольник,
площадь образца. Затем откройте диалоговое окно Ranked Set Sampling и введите
следующие значения на странице Costs:
Стоимость рейтинга за местоположение: 25.00
Введите следующие значения на странице Выборка ранжированного набора:
Распределение лабораторных данных: Симметричный
Метод ранжирования: профессиональное суждение
Размер набора: 3
Выберите: Двусторонний доверительный интервал О
Среднее
Уровень достоверности: 95%
Максимально допустимая полуширина доверительного интервала: 5,5
Расчетное стандартное отклонение: 20
Обратите внимание на следующие выходные данные в правом нижнем углу диалогового окна:
Выбранный размер комплекта (м): 3
Количество циклов (r): 10
Требуемое количество образцов (m x r): 30
Количество полевых локаций для ранжирования (m x m x r): 90
Нажмите кнопку «Применить», и вы увидите все 90 местоположений ранжирования полей.

отображается на карте, похожей на следующую цифру:
Различные цвета обозначают разные циклы. Используйте рейтинговый набор
Панель инструментов для выбора первого цикла. Вы увидите местоположения полей, которые
представляют первый цикл, подобный следующему рисунку:
Квадраты представляют собой первый набор местоположений полей. Три дерева
ближайший к этим местам на карте будет оцениваться и самый маленький
дерево будет выбрано для выборки (керновым методом или каким-либо другим методом). Треугольники
представляют второй набор местоположений полей. Три ближайших дерева
эти места на карте будут оценены, и дерево среднего размера будет
быть выбраны для выборки. Наконец, круги представляют третий набор
расположение полей в первом цикле. Три ближайших к этим местам дерева
на карте будет оцениваться, и будет взято самое большое дерево.
Этот процесс будет повторяться для второго цикла. Полевые локации
связанные со вторым циклом, представлены следующим рисунком:
Один и тот же процесс будет повторяться для всех 10 циклов. В конце
В конце
за 10 циклов вы соберете 30 образцов, по 3 из каждого цикла.
Средний возраст, указанный в этих выборках, с вероятностью 95% будет
в течение 5,5 лет от фактического среднего возраста деревьев на участке
(если ваши предположения разумны: стандартное отклонение за 20 лет и т. д.)
Реализация примера в виде несбалансированного (асимметричного) дизайна в ВСП
Предположим, что было замечено, что больше деревьев старше, чем
моложе, в результате чего население смещается в сторону более старших возрастов. Это указывало бы
потребность в несбалансированном ранжированном наборе выборок. В несбалансированном
дизайн, высший ранг может быть отобран более одного раза, чтобы лучше
определить среднее значение, когда больше значений в популяции находятся ближе к вершине
распределения.
В VSP начните с пустого проекта и нарисуйте прямоугольник,
площадь образца. Затем откройте диалоговое окно Ranked Set Sampling и введите
следующие значения на странице Costs:
Стоимость рейтинга за местоположение: 25. 00
00
Введите следующие значения на странице Выборка ранжированного набора:
Распределение лабораторных данных: асимметричное (смещено в
Высокий)
Метод ранжирования: профессиональное суждение
Размер комплекта: 3
Уровень достоверности: 95%
Максимально допустимая разница в % между расчетным средним значением и истинным средним значением:
15
Стандартное геометрическое отклонение: 1,5
Обратите внимание на следующие выходные данные в правом нижнем углу диалогового окна:
Выбранный размер комплекта [м]: 3
Количество циклов [об]: 6
Количество наборов для высшего разряда [t]: 2
Количество наборов за цикл [m+t-1]: 4
Требуемое количество выборок [(m+t-1) x r]: 24
Количество полей для ранжирования [(m+t-1) x m x r]: 72
Нажмите кнопку «Применить», и вы увидите все 72 места ранжирования полей.
отображается на карте, похожей на следующую цифру:
Различные цвета обозначают разные циклы.
 Используйте рейтинговый набор
Используйте рейтинговый набор
Панель инструментов для выбора первого цикла. Вы увидите местоположения полей, которые
представляют первый цикл, подобный следующему рисунку:
Квадраты представляют собой первый набор местоположений полей. Три дерева
ближайший к этим местам на карте будет оцениваться и самый маленький
дерево будет выбрано для выборки (керновым методом или каким-либо другим методом). Треугольники
представляют второй набор местоположений полей. Три ближайших дерева
эти места на карте будут оценены, и дерево среднего размера будет
быть выбраны для выборки. Кружки обозначают высший ранг. Заметить, что
есть два набора кругов: один набор сопровождается цифрой 1, а другой набор сопровождается цифрой 2. Это потому, что высший ранг должен быть
выбран дважды для этого несбалансированного плана (t = 2). Круг-1 представляет
третий набор местоположений полей в первом цикле. Три ближайших дерева
эти места на карте будут оценены, и самое большое дерево будет
быть опробованным. Наконец, круги-2 представляют собой четвертый набор местоположений полей.
Наконец, круги-2 представляют собой четвертый набор местоположений полей.
в первом цикле. Три ближайших к этим местам дерева на карте
будет оцениваться, и, опять же, будет отобрано самое большое дерево.
Этот процесс будет повторяться для второго цикла. Полевые локации
связанные со вторым циклом, представлены следующим рисунком:
Один и тот же процесс будет повторяться для всех 6 циклов. В конце
6 циклов, вы соберете 24 образца, по 4 из каждого цикла. Значение
возраст, указанный в этих образцах, с вероятностью 95% будет находиться в пределах
15% от фактического среднего возраста деревьев на этом участке (если ваши предположения
разумны: 1,5 геометрического стандартного отклонения и т. д.)
Определение количества выборок
Существует 2 основных типа дизайна для RSS: сбалансированный и несбалансированный дизайн.
Сбалансированные планы предполагают, что интересующие аналитические измерения
симметрично распределены относительно среднего. Несбалансированные конструкции предполагают, что
Несбалансированные конструкции предполагают, что
распределение измерений смещено в сторону более высоких значений. несбалансированный
дизайны выбирают больше выборок из верхнего ранга, чтобы лучше оценить среднее значение
учитывая неравномерность данных.
Определение количества циклов и, следовательно, количества местоположений
для ранжирования и количество местоположений, которые необходимо измерить, представляет собой пятиэтапный процесс:
Шаг 1. Определите размер выборки, предполагая, что простая случайная выборка
используется.
Для сбалансированных планов количество выборок, необходимое для простого случайного
выборка (\(n_0\)) рассчитывается с помощью ВСП с использованием либо одностороннего, либо
двустороннее уравнение доверительного интервала, выбранное пользователем ВСП. 92$$
где
\(n_0\) | — рекомендуемое минимальное количество образцов для исследования |
\(с\) | – оценочное стандартное отклонение измерений собранных |
\(д\) | — максимальная желаемая ширина (или полуширина) достоверности |
\(t_{1-\alpha,df}\) | — значение t-распределения Стьюдента с \(n\)-1 |
\(t_{1-\alpha/2,df}\) | — значение t-распределения Стьюдента с \(n\)-1 |
Поскольку \(n\) появляется в обеих частях приведенных выше уравнений (справа
сторона появляется в степенях свободы t-распределения),
уравнение необходимо решать итеративно. VSP делает это автоматически, используя
схема итераций в (Gilbert 1987, стр. 32).
Для несбалансированных планов количество выборок вычисляется с помощью
Изложен метод скорректированной классической формулы
by (Перес и Лефанте 19{ln(GSD)}-1)$$
где
\(n_{\text{классический}}\) | — приблизительное рекомендуемое минимальное количество образцов, |
\(Z_{1-\alpha/2}\) | — значение стандартного нормального распределения, такое что |
\(GSD\) | — геометрическое стандартное отклонение, |
\(пер. | — натуральный логарифм, а |
\(\пи\) | — максимальная пропорциональная разница между расчетным |
Затем линейная регрессия используется для расчета рекомендуемого минимума
число выборок по следующей формуле: $$n_0 = \beta_0 + \beta_1(n_{\text{classic}})$$
где
\(n_0\) | — количество образцов, необходимое для простой случайной выборки, |
\(\бета_0\) | — Y-пересечение формулы регрессии, |
\(\бета_1\) | — наклон формулы регрессии. |
\(\beta_0\) –
получено из следующей таблицы [из таблицы III в (Perez
и Лефанте 1997, стр.2791)]:
Уровень достоверности | GSD = 1,1 | GSD = 1,5 | GSD = 2,0 | GSD = 2,5 | НГД = 3,0 | GSD = 3,5 | GSD = 4,0 |
90% | 2,9532 | 7. | 11.3183 | 15,5638 | 20.1322 | 25.9327 | 30.3223 |
95% | 3.3331 | 7,9237 | 14.0744 | 20.5406 | 27.1563 | 33.6865 | 40.1084 |
99% | 4,9265 | 11.2470 | 20.5069 | 30.2478 | 40.1743 | 51.1945 | 60.6576 |
\(\beta_1\) получается из следующей таблицы [из Таблицы III в
(Перес и Лефанте 1997, стр.2791)]:
Уровень достоверности | GSD = 1,1 | GSD = 1,5 | GSD = 2,0 | GSD = 2,5 | НГД = 3,0 | GSD = 3,5 | GSD = 4,0 |
90% | 0,4714 | 0,6926 | 0,8509 | 0,8794 | 0,8499 | 0,7731 | 0,7033 |
95% | 0,4726 | 0,8094 | 0,9046 | 0,9129 | 0,8731 | 0,8072 | 0,7288 |
99% | 0,4740 | 0,8865 | 0,9808 | 0,9877 | 0,9444 | 0,8612 | 0,7796 |
Шаг 2: Выберите значение для установленного размера, м.
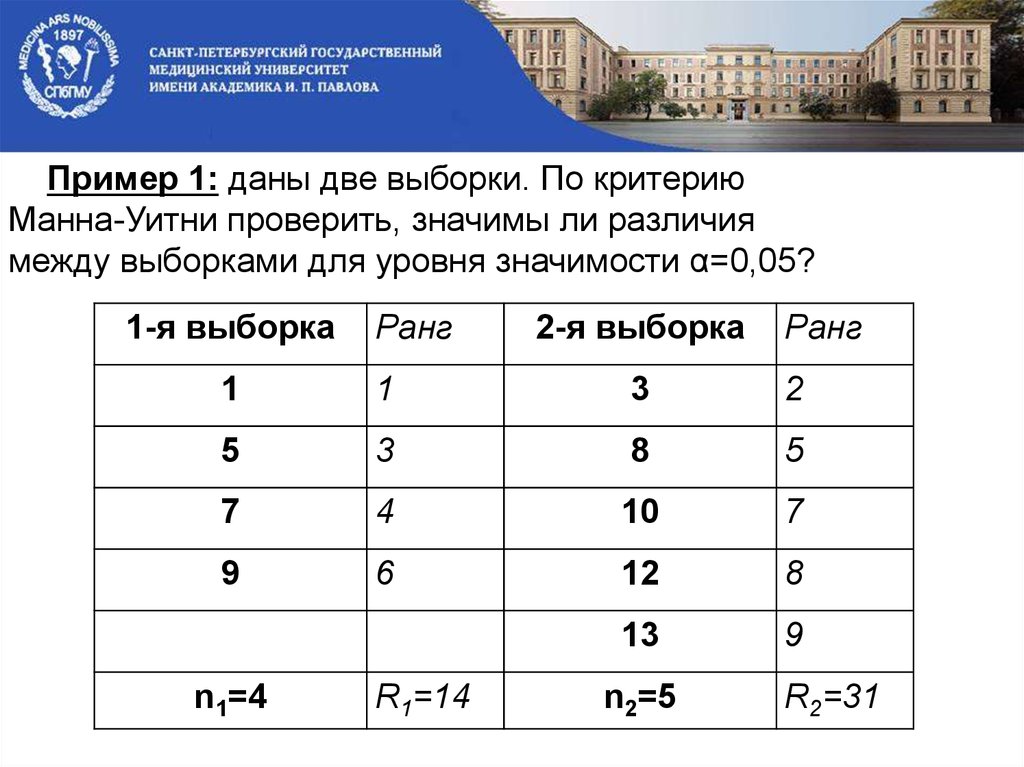
Это значение обычно основано на практических ограничениях ранжирования местоположений.
в полевых условиях с использованием профессионального суждения или полевых скрининговых измерений.
Может быть трудно использовать профессиональное суждение для точного ранжирования по
глаз более чем в 4 или 5 местах. Другие ограничения, которые могут повлиять на
Размер m — время, персонал и затраты. VSP ограничивает m до 5
для отбора проб и 8 для полевых скрининговых измерений.
Шаг 3: Определите относительную точность.
Для расчета количества циклов требуется относительная точность. Для сбалансированных конструкций относительная точность RP находится из следующего
таблица, предполагающая, что данные нормально распределены [из Таблицы 1 (Patil et. al. 1994, pg.176)]:
Размер набора = 2 | Размер набора = 3 | Размер набора = 4 | Размер набора = 5 |
1,467 | 1,914 | 2,347 | 2,770 |
Если размер набора, m, больше 5, RP находится с использованием следующего
линейная формула:
\(RP = 0,4342м + 0,6048\)
Для несбалансированных конструкций RP определяется из следующей таблицы, при условии, что
данные распределены логнормально [из таблицы 1
(Патил и др. 1994, стр. 177)]:
1994, стр. 177)]:
Размер набора | КВ = 0,1 | КВ = 0,202 | КВ = 0,307 | КВ = 0,416 | КВ = 0,533 | КВ = 0,658 | КВ = 0,795 | КВ = 0,947 | CV = 1,117 | КВ = 1,311 | |||||||||||||||||||
2 | 1,46 | 1,45 | 1,42 | 1,40 | 1,37 | 1,33 | 1,29 | 1,26 | 1,22 | 1,19 | |||||||||||||||||||
3 | 1,90 | 1,87 | 1,83 | 1,77 | 1,70 | 1,62 | 1,55 | 1,47 | 1,40 | 1,34 | |||||||||||||||||||
4 | 2,33 | 2,28 | 2. | 2.11 | 2,00 | 1,89 | 1,78 | 1,67 | 1,56 | 1,47 | |||||||||||||||||||
5 | 2,75 | 2,68 | 2,57 | 2,44 | 2,29 | 2,14 | 1,99 | 1,84 | 1,71 | 1,59 | |||||||||||||||||||
6 | 3,15 | 3,07 | 2,93 | 2,76 | 2,57 | 2,37 | 2,18 | 2,00 | 1,84 | 1,70 | |||||||||||||||||||
7 | 3,56 | 3,45 | 3,28 | 3,07 | 2,83 | 2,60 | 2,40 | 2,16 | 1,96 | 1,80 | |||||||||||||||||||
8 | 3,95 | 3,86 | 3,61 | 3,36 | 3,09 | 2,81 | 2,55 |
Резюме | 0,25 | 0,5 | 1,0 | 1,25 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 |
\(т\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Общее количество выборок \(n\) находится по следующей формуле:
\(n = rx(m+t-1)\)
Количество полевых местоположений, которые необходимо ранжировать, чтобы получить n выборок
это:
\(г*м*(м+т-1)\)
Образцы ранжированного набора
Для ранжированной выборки ВСП создает маркеры полевой выборки на карте.
которые имеют разную форму и цвет.
Цвет маркера указывает на его цикл. Цвета цикла начинаются
на красный и пройти по спектру до фиолетового. Используйте цикл
выпадающий список в выборке ранжированного набора
Панель инструментов для отображения только местоположений полей для определенного цикла.
Форма маркера указывает на его набор. Местоположения полевых образцов для
первый набор отмечен квадратами, места для второго набора
отмечены треугольниками и т. д. Для несбалансированных конструкций отбирается верхний набор
несколько раз, так что число сопровождает эти маркеры. Используйте набор
выпадающий список в выборке ранжированного набора
Панель инструментов для отображения только местоположений полей для определенного набора.
Ранжированные наборы местоположений отбора проб в полевых условиях генерируются с меткой, имеющей
следующий формат:
\(RSS-c-s-i\)
где
\(c\) указывает номер цикла
\(s\) указывает номер комплекта (для несбалансированных конструкций этот номер
также увеличивается для каждой итерации верхнего набора)
\(i\) — уникальный идентификатор в наборе
Используйте команду View Labels на
меню или панель инструментов, чтобы показать или скрыть метки для выборки поля
места. 92\), является разумным и репрезентативным
92\), является разумным и репрезентативным
выборки населения (используется для вычисления \(n_0\)).
3. Распределение данных симметрично и приблизительно нормально распределено
(используется для определения РП).
4. Оценка выборочного среднего разумна и репрезентативна
выборки населения.
5. Поля, которые будут ранжированы, выбираются с помощью простого
случайная выборка.
Первые три предположения будут оцениваться при сборе данных после
анализ. Четвертое предположение справедливо, поскольку выборочное среднее будет
быть несмещенной оценкой среднего значения генеральной совокупности. Ответственность за выполнение пятого допущения лежит на исследователях.
Для иллюстрации выборки ранжированных наборов см. Ранжированные выборки.
Установите сэмплирование в главе 3 Руководства пользователя VSP.
Каталожные номера:
EPA, ноябрь 2001 г. Руководство
для выбора плана выборки для сбора экологических данных,
EPA QA/G-5S, проект экспертной оценки, Вашингтон, округ Колумбия,
Гилберт, Р. О. 1987. Статистический
О. 1987. Статистический
Методы мониторинга загрязнения окружающей среды. Джон Уайли и
Сыновья, Нью-Йорк.
Макинтайр, Г.А. 1952. А
метод несмещенной выборочной выборки с использованием ранжированных наборов, австралийский
Журнал сельскохозяйственных исследований 3:385-390.
Патил, Г.П., А.К. Синха и К. Тайлли. 1994.
Выборка ранжированного набора, Справочник по статистике
12, Статистика окружающей среды, стр. 167-200, (Г. П. Патил и Ч. Р. Рао, редакторы),
Северная Голландия, Нью-Йорк, штат Нью-Йорк.
Перес, А. и Дж.Дж. Лефанте. 1997. Определение размера выборки и влияние цензуры.
при оценке среднего арифметического логнормального распределения.
Коммуникации в статистике, теории и методах 26 (11): 2779-2801.
Диалоговое окно выборки ранжированного множества содержит следующие элементы управления:
Параметры экономической эффективности
Для профессионального суждения:
Для экранирующих измерений в полевых условиях:
Размер комплекта
Параметры простой случайной выборки
Для симметричных конструкций:
За одностороннюю уверенность
Интервал :
Максимально допустимая ширина достоверности
Интервал
Для двусторонней уверенности
Интервал :
Расчетное стандартное отклонение
Для асимметричных конструкций:
Максимально допустимая разница в %
между расчетным средним и истинным средним
Геометрическое стандартное отклонение
Страница стоимости
См. также: Панель инструментов выборки рангового набора
также: Панель инструментов выборки рангового набора
Выборка ранжированного набора
Меню сайта:
- Главная
- Обучение
- Исследования
- Программное обеспечение
- Публикации
- Редактирование
- Ссылки
Выборка ранжированного множества
Выборка ранжированного набора является альтернативой простой случайной выборке.
что иногда может значительно улучшить точность. Это было
первоначально предложено в связи с оценкой урожайности травостоя
в статье Г. А. Макинтайра [ссылка 1].
В последние годы он стал применяться, в частности, к проблемам в
наука об окружающей среде. В настоящее время существует довольно большая литература,
большая часть этого обобщена в монографии Чена, Бай и Синхи.
[Ссылка 2].
Вот еще
хорошее введение
[Ссылка 3].
Я впервые столкнулся с этой техникой много лет назад, тоже в
связи с оценкой урожая травостоя [ссылки 4,5].
Несколько лет спустя я снова заинтересовался ранжированной множественной выборкой.
после я
принимал участие в оценке метода оценки
распыление отложений на листьях плодовых деревьев. На этой странице представлены
краткое описание данной работы со ссылками на публикации и
исходные данные.
Оценка отложений при распылении
Переменная
здесь интерес представляет осадок на единицу площади листа. Этот
требует умеренного времени для точного измерения, но если уходит
распыляют флуоресцентную краску, образующиеся отложения могут
оцениваться визуально в ультрафиолетовом свете. Пример изображения
показано справа.
Оценочное исследование
Для нашего оценочного исследования мы использовали две разные настройки опрыскивателя.
от каждого отобрали по 125 листьев. В лаборатории каждый набор из 125 штук был случайным образом
разделены на 25 наборов по 5. Затем четыре разных ранжировщика оценили оба
верхняя и нижняя поверхности листа в каждом наборе. Это было повторено
Это было повторено
с разной рандомизацией, для выдачи большого количества информации
об ошибках ранжирования.
Для этого оценочного исследования были измерены все листья. Чтобы получить
«истинное» измерение для каждой поверхности листа, мы использовали систему анализа изображений, чтобы
получить общее значение шкалы серого пикселя. Затем это было разделено на
площадь листа, чтобы дать меру плотности отложений.
Это исследование было проведено с доктором Роем Мюрреем из East Malling Research.
Результаты
В этом исследовании два фактора снижают потенциальные преимущества ранжирования.
установить выборку по отношению к простой случайной выборке:
* стоимость сбора дополнительных листов и ранжирования их;
* ошибки, возникающие в процессе ранжирования
При учете этих факторов относительная точность
выборки ранжированного набора оценивается примерно в 1,5 раза — в других
слов примерно на 50% больше образцов потребуется для достижения
с той же точностью при использовании обычной случайной выборки.
Между разными рейтингами была разумная согласованность.
(коэффициент конкордации Кендалла был около 0,9) и оценки
относительной точности были одинаковыми для всех четырех ранжировщиков. И не было
существует большая разница в относительной точности между верхним
и нижней поверхности листа или между двумя различными настройками опрыскивателя.
Более подробное описание этой работы было опубликовано в
документ конференции.
Вы можете загрузить необработанные данные из этого исследования
как текстовый файл.
В
неопубликованная статья
Я использовал обобщение модели Маллоуза, чтобы исследовать
ошибки ранжирования, допущенные четырьмя ранжировщиками [Ссылка 7].
Несколько измерений
Специфической проблемой, возникающей при отложениях в результате распыления, является необходимость
для сбора данных по обеим листовым поверхностям. Отложения на двух поверхностях
имеют тенденцию к слабой отрицательной корреляции — если лист оказывается
ориентированы так, чтобы на одну поверхность попадало много брызг, а на другую
поверхность имеет тенденцию получать низкий депозит.
Если листья выбираются на основе их ранжирования только на одном
поверхности, полученный образец может быть очень неуравновешенным в отношении
к его ранжированию на другой поверхности. Это приводит к потере эффективности.
Однако простой эвристический алгоритм, который можно реализовать
без особых дополнительных усилий, гарантирует, что листья
разумно сбалансированы относительно их рангов на обеих поверхностях.
Я кратко рассказал об этой работе в самом
приятный, расширенный семинар SPRUCE на Окружающая среда
Отбор проб и мониторинг проведен в
Эшторил, Португалия, 22–24 марта 2001 г.
письменная версия
впоследствии был опубликован в журнале Environmental & Ecological
Статистика [Ссылка 8].
Ссылки
[1] McIntyre, G.A. (1952) Метод объективной выборочной выборки.
с помощью ранжированных наборов. Австралийский журнал сельскохозяйственных исследований ,
3 , 385-390.
[2] Чен З., Бай З. и Синха Б.

 Если
Если


 \)
\) 5249
5249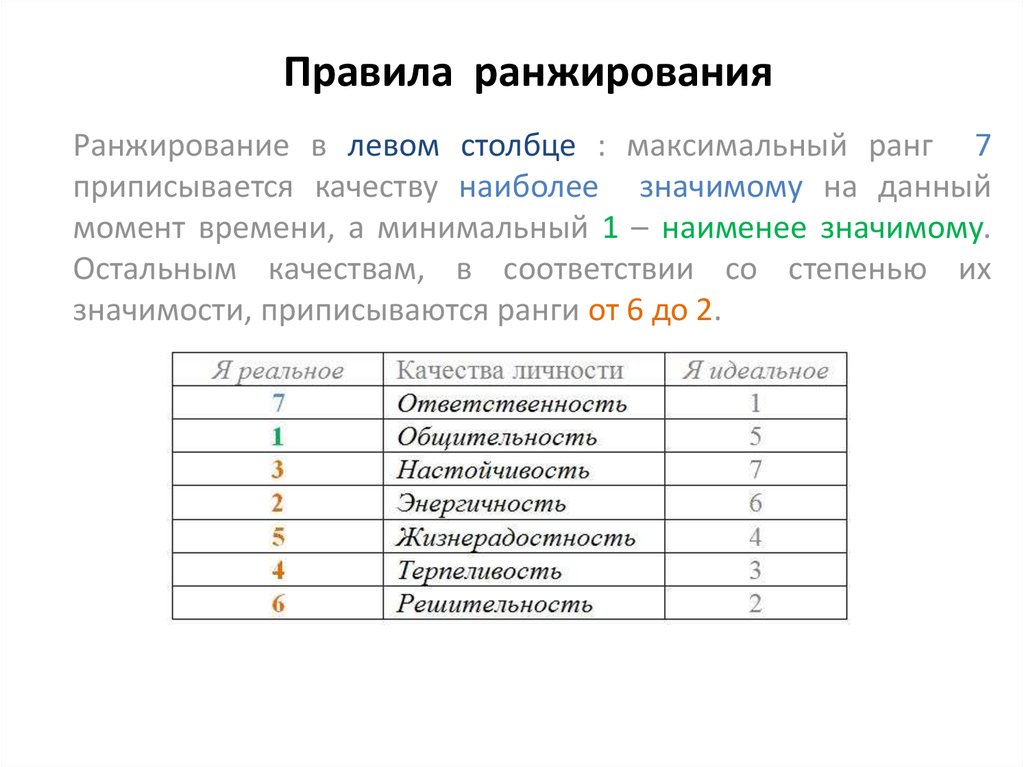 21
21