Содержание
Метрики качества ранжирования / Хабр
В процессе подготовки задачи для вступительного испытания на летнюю школу GoTo, мы обнаружили, что на русском языке практически отсутствует качественное описание основных метрик ранжирования (задача касалась частного случая задачи ранжирования — построения рекомендательного алгоритма). Мы в E-Contenta активно используем различные метрики ранжирования, поэтому решили исправить это недоразуменее, написав эту статью.
Задача ранжирования сейчас возникает повсюду: сортировка веб-страниц согласно заданному поисковому запросу, персонализация новостной ленты, рекомендации видео, товаров, музыки… Одним словом, тема горячая. Есть даже специальное направление в машинном обучении, которое занимается изучением алгоритмов ранжирования способных самообучаться — обучение ранжированию (learning to rank). Чтобы выбрать из всего многообразия алгоритмов и подходов наилучший, необходимо уметь оценивать их качество количественно. О наиболее распространенных метриках качества ранжирования и пойдет речь далее.
О наиболее распространенных метриках качества ранжирования и пойдет речь далее.
Кратко о задаче ранжирования
Ранжирование — задача сортировки набора элементов из соображения их релевантности. Чаще всего релевантность понимается по отношению к некому объекту. Например, в задаче информационного поиска объект — это запрос, элементы — всевозможные документы (ссылки на них), а релевантность — соответствие документа запросу, в задаче рекомендаций же объект — это пользователь, элементы — тот или иной рекомендуемый контент (товары, видео, музыка), а релевантность — вероятность того, что пользователь воспользуется (купит/лайкнет/просмотрит) данным контентом.
Формально, рассмотрим N объектов и M элементов . Реузальтат работы алгоритма ранжирования элементов для объекта — это отображение , которое сопоставляет каждому элементу вес , характеризующей степень релевантности элемента объекту (чем больше вес, тем релевантнее объект).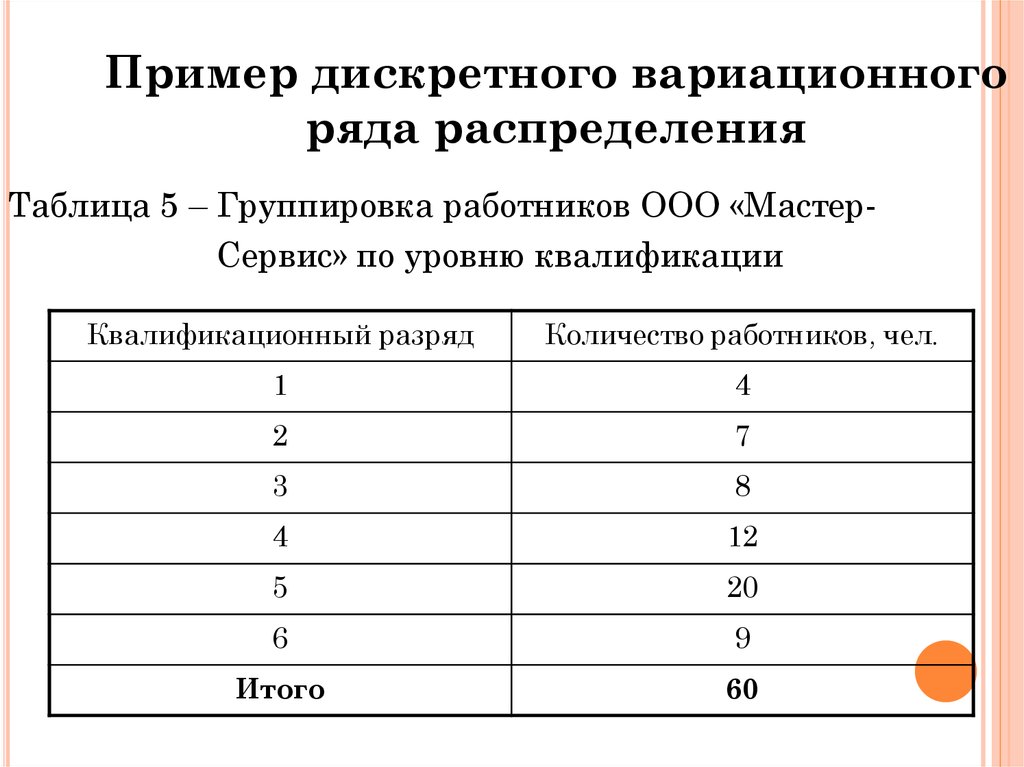 При этом, набор весов задает перестановку на наборе элементов элементов (считаем, что множество элементов упорядоченное) исходя из их сортировки по убыванию веса .
При этом, набор весов задает перестановку на наборе элементов элементов (считаем, что множество элементов упорядоченное) исходя из их сортировки по убыванию веса .
Чтобы оценить качество ранжирования, необходимо иметь некоторый «эталон», с которым можно было бы сравнить результаты алгоритма. Рассмотрим — эталонную функцию релевантности, характеризующую «настоящую» релевантность элементов для данного объекта ( — элемент идеально подходит, — полностью нерелевантен), а так же соответствующую ей перестановку (по убыванию ).
Существует два основных способа получения :
1. На основе исторических данных. Например, в случае рекомендаций контента, можно взять просмотры (лайки, покупки) пользователя и присвоить просмотренным весам соответствующих элементов 1 ( ), а всем остальным — 0.
2. На основе экспертной оценки. Например, в задаче поиска, для каждого запроса можно привлечь команду асессоров, которые вручную оценят релевантности документов запросу.
Стоит отметить, что когда принимает только экстремальные значения: 0 и 1, то престановку обычно не рассматривют и учитывают лишь множество релевантных элементов, для которых .
Цель метрики качества ранжирования — определить, насколько полученные алгоритмом оценки релевантности и соответствующая им перестановка соответствуют истинным значениям релевантности . Рассмотрим основные метрики.
Mean average precision
Mean average precision at K (map@K) — одна из наиболее часто используемых метрик качества ранжирования. Чтобы разобраться в том, как она работает начнем с «основ».
Замечание: «*precision» метрики используется в бинарных задачах, где принимает только два значения: 0 и 1.
Precision at K
Precision at K (p@K) — точность на K элементах — базовая метрика качества ранжирования для одного объекта. Допустим, наш алгоритм ранжирования выдал оценки релевантности для каждого элемента . Отобрав среди них первые элементов с наибольшим можно посчитать долю релевантных. Именно это и делает precision at K:
Замечание: под понимается элемент , который в результате перестановки оказался на -ой позиции. Так, — элемент с наибольшим , — элемент со вторым по величине и так далее.
Так, — элемент с наибольшим , — элемент со вторым по величине и так далее.
Average precision at K
Precision at K — метрика простая для понимания и реализации, но имеет важный недостаток — она не учитывает порядок элементов в «топе». Так, если из десяти элементов мы угадали только один, то не важно на каком месте он был: на первом, или на последнем, — в любом случае . При этом очевидно, что первый вариант гораздо лучше.
Этот недостаток нивелирует метрика ранжирования average precision at K (ap@K), которая равна сумме p@k по индексам k от 1 до K только для релевантных элементов, деленому на K:
Так, если из трех элементов мы релевантным оказался только находящийся на последнем месте, то , если угадали лишь тот, что был на первом месте, то , а если угаданы были все, то .
Теперь и map@K нам по зубами.
Mean average precision at K
Mean average precision at K (map@K) — одна из наиболее часто используемых метрик качества ранжирования..jpg) В p@K и ap@K качество ранжирования оценивается для отдельно взятого объекта (пользователя, поискового запроса). На практике объектов множество: мы имеем дело с сотнями тысяч пользователей, миллионами поисковых запросов и т.д. Идея map@K заключается в том, чтобы посчитать ap@K для каждого объекта и усреднить:
В p@K и ap@K качество ранжирования оценивается для отдельно взятого объекта (пользователя, поискового запроса). На практике объектов множество: мы имеем дело с сотнями тысяч пользователей, миллионами поисковых запросов и т.д. Идея map@K заключается в том, чтобы посчитать ap@K для каждого объекта и усреднить:
Замечание: идея эта вполне логична, если предположить, что все пользователи одинаково нужны и одинаково важны. Если же это не так, то вместо простого усреднения можно использовать взвешенное, домножив ap@K каждого объекта на соответствующий его «важности» вес.
Normalized Discounted Cumulative Gain
Normalized discounted cumulative gain (nDCG) — еще одна распространенная метрика качества ранжирования. Как и в случае с map@K, начнем с основ.
Cumulative Gain at K
Вновь рассмотрим один объект и элементов с наибольшим . Cumulative gain at K (CG@K) — базовая метрика ранжирования, которая использует простую идею: чем релевантные элементы в этом топе, тем лучше:
Эта метрика обладает очевидными недостатками: она не нормализована и не учитывает позицию релевантных элементов.
Заметим, что в отличии от p@K, CG@K может использоваться и в случае небинарных значений эталонной релевантности .
Discounted Cumulative Gain at K
Discounted cumulative gain at K (DCG@K) — модификация cumulative gain at K, учитывающая порядок элементов в списке путем домножения релевантности элемента на вес равный обратному логарифму номера позиции:
Замечание: если принимает только значения 0 и 1, то , и формула принимает более простой вид:
Использование логарифма как функции дисконтирования можно объяснить следующими интуитивными соображениями: с точки зрения ранжирования позиции в начале списка отличаются гораздо сильнее, чем позиции в его конце. Так, в случае поискового движка между позициями 1 и 11 целая пропасть (лишь в нескольких случаях из ста пользователь заходит дальшей первой страницы поисковой выдачи), а между позициями 101 и 111 особой разницы нет — до них мало кто доходит. Эти субъективные соображения прекрасно выражаются с помощью логарифма:
Эти субъективные соображения прекрасно выражаются с помощью логарифма:
Discounted cumulative gain решает проблему учета позиции релевантных элементов, но лишь усугубляет проблему с отсутствием нормировки: если варьируется в пределах , то уже принимает значения на не совсем понятно отрезке. Решить эту проблему призвана следующая метрика
Normalized Discounted Cumulative Gain at K
Как можно догадаться из названия, normalized discounted cumulative gain at K (nDCG@K) — не что иное, как нормализованная версия DCG@K:
где — это максимальное (I — ideal) значение . Так как мы договорились, что принимает значения в , то .
Таким образом, наследует от учет позиции элементов в списке и, при этом принимает значения в диапазоне от 0 до 1.
Замечание: по аналогии с map@K можно посчитать , усредненный по всем объектам.
Mean reciprocal rank
Mean reciprocal rank (MRR) — еще одна часто используемая метрика качества ранжирования. Задается она следующей формулой:
Задается она следующей формулой:
где — reciproсal rank для -го объекта — очень простая по своей сути величина, равная обратному ранку первого правильно угаданного элемента.
Mean reciprocal rank изменяется в диапазоне [0,1] и учитывает позицию элементов. К сожалению он делает это только для одного элемента — 1-го верно предсказанного, не обращая внимания на все последующие.
Метрики на основе ранговой корреляции
Отдельно стоит выделить метрики качества ранжирования, основанные на одном из коэффициентов ранговой корреляции. В статистике, ранговый коэффициент корреляции — это коэффициент корреляции, который учитывает не сами значения, а лишь их ранг (порядок). Рассмотрим два наиболее распространенных ранговых коэффициента корреляции: коэффициенты Спирмена и Кендэлла.
Ранговый коэффициент корреляции Кендэлла
Первый из них — коэффициент корреляции Кендэлла, который основан на подсчете согласованных
(и несогласованных) пар у перестановок — пар элементов, котором перестановки присвоили одинаковый (разный) порядок:
Ранговый коэффициент корреляции Спирмена
Второй — ранговый коэффициент корреляции Спирмена — по сути является ни чем иным как корреляции Пирсона, посчитанной на значениях рангов.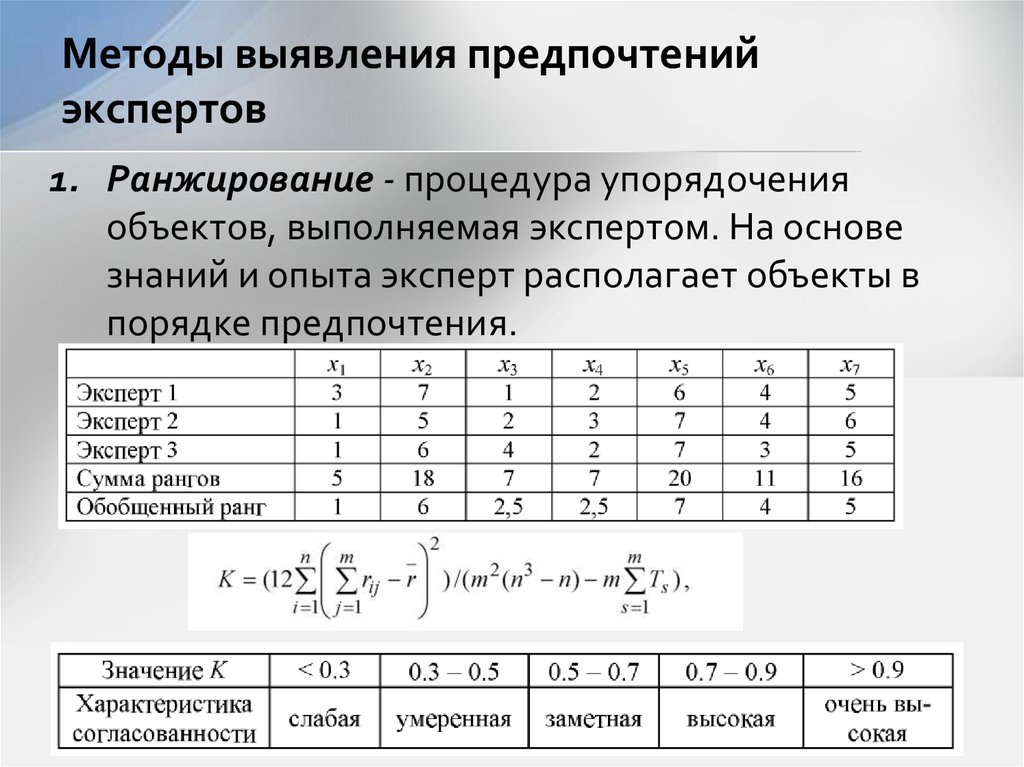 Есть достаточно удобная формула, выражающая его из рангов напрямую:
Есть достаточно удобная формула, выражающая его из рангов напрямую:
где — коэффициент корреляции Пирсона.
Метрики на основе ранговой корреляции обладают уже известными нам недостатком: они не учитывают позицию элементов (еще хуже чем p@K, т.к. корреляция считается по всем элементам, а не по K элементам с наибольшим рангом). Поэтому на практике используются крайне редко.
Метрики на основе каскадной модели поведения
До этого момента мы не углублялись в то, как пользователь (далее мы рассмотрим частный случай объекта — пользователь) изучает предложенные ему элементы. На самом деле, неявно нами было сделано предположение, что просмотр каждого элемента независим от просмотров других элементов — своего рода «наивность». На практике же, элементы зачастую просматриваются пользователем поочередно, и то, просмотрит ли пользователь следующий элемент, зависит от его удовлетворенности предыдущими. Рассмотрим пример: в ответ на поисковый запрос алгоритм ранжирования предложил пользователю несколько документов. Если документы на позиции 1 и 2 оказались крайне релевантны, то вероятность того, что пользователь просмотрит документ на позиции 3 мала, т.к. он будет вполне удовлетворен первыми двумя.
Рассмотрим пример: в ответ на поисковый запрос алгоритм ранжирования предложил пользователю несколько документов. Если документы на позиции 1 и 2 оказались крайне релевантны, то вероятность того, что пользователь просмотрит документ на позиции 3 мала, т.к. он будет вполне удовлетворен первыми двумя.
Подобные модели поведения пользователя, где изучение предложенных ему элементов происходит последовательно и вероятность просмотра элемента зависит от релевантности предыдущих называются каскадными.
Expected reciprocal rank
Expected reciprocal rank (ERR) — пример метрики качества ранжирования, основанной на каскадной модели. Задается она следующей формулой:
где ранг понимается по порядку убывания . Самое интересное в этой метрике — вероятности. При их расчете используются предположения каскадной модели:
где — вероятность того, что пользователь будет удовлетворен объектом с рангом . Эти вероятности считаются на основе значений . Так как в нашем случае , то можем рассмотреть простой вариант:
Эти вероятности считаются на основе значений . Так как в нашем случае , то можем рассмотреть простой вариант:
который можно прочесть, как: истинная релевантность элемента оказавшегося на позиции после сортировки по убыванию .
В общем же случае чаще всего используют следующую формулу:
PFound
PFound — метрика качества ранжирования, предложенная нашими соотечественниками и использующая похожую на каскадную модель:
где
- ,
- , если и 0 иначе,
- — вероятность того, что пользователь прекратит просмотр по внешним причинам.
В заключении приведем несколько полезных ссылок по теме:
— Статьи на википедии по: обучению ранжированию, MRR, MAP и nDCG.
— Официальный список метрик используемых на РОМИП 2010.
— Описание метрик MAP и nDCG на kaggle. com.
com.
— Оригинальные статьи по каскадной модели, ERR и PFound.
Написано с использованием StackEdit.
Большое спасибо пользователю SeptiM за восхитительный habratex.
Как посчитать ранг в статистике — Dudom
Назначение сервиса . С помощью данного онлайн-калькулятора производится:
- сортировка данных по возрастанию или убыванию;
- присваивание ранга;
- Решение онлайн
- Видеоинструкция
- Оформление Word
Пример . Проранжировать эти данные, присваивая 1 ранг наибольшему значению и записать в виде таблицы.
Уважаемые посетители Портала Знаний, если Вы найдете ошибку в тексте, выделите, пожалуйста, ее мышью и нажмите Сtrl+Enter. Мы обязательно исправим текст!
Средний ранг
Пусть имеется выборка из n наблюдений
. Упорядочим выборку по возрастанию: . Предположим, что наблюдение имеет ту же величину, что и (совпадающие с ним) некоторые из остальных Z наблюдений.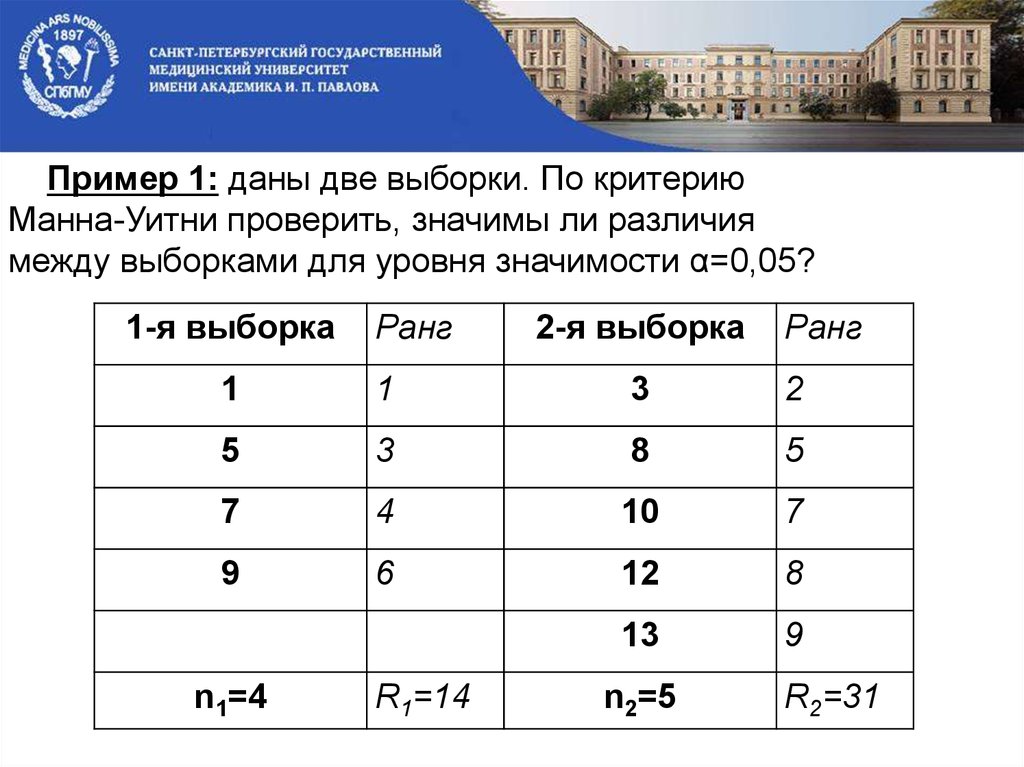
Средний ранг
в ранжировке наблюдений есть среднее арифметическое из рангов, которые были бы назначены и остальным значениям Z, таким же, что и , если бы равные наблюдения оказались различными.
Пример. Ранжируем выборку из пяти наблюдений (11,12,14,14,14). Значение «14» встречается в ней 3 раза. Если бы равные наблюдения мы считали различными, то набор рангов для этой выборки был бы (1,2,3,4,5). Поскольку все значения «14» равноправны, присваиваем им усреднённый ранг (3+4+5)/3=4 и получаем набор рангов (1,2,4,4,4).
Синоним: midrank – средний ранг, срединный ранг.
Ранжирование по cm олбцам
Пример 1.3. Результаты тестирования двух группы испытуемых по 5 человек в каждой по методике дифференциальной диагностики депрессивных состояний В. А. Жмурова представлены в табл. 1.3.
Перед психологом стоит задача: проранжировать обе группы испытуемых как одну, т.е. объединить выборки и проставить ранги объединенной выборке, сохраняя, однако, различие между группами. Сделаем это в табл. 1.4, причем так, что максимальной величине будем ставить минимальный ранг — 1. Ранжируем.
Сделаем это в табл. 1.4, причем так, что максимальной величине будем ставить минимальный ранг — 1. Ранжируем.
Проверим правильность ранжирования. Поскольку у нас уже получены суммы рангов по столбцам, то общую сумму рангов можно получить, просто сложив эти суммы. Итак, 31 + 24 = 55.
Чтобы применить формулу (1.1), нужно подсчитать общее количество испытуемых — это 5 + 5 = 10. Тогда по формуле (1.1) получаем
Следовательно, ранжирование проведено правильно.
В том случае, если в таблице имеется большое количество строк и столбцов, то для подсчета суммы рангов в таблице можно использовать модификацию формулы (1.1), она будет выглядеть так:
где к — число строк, с — число столбцов.
Вычислим сумму рангов по формуле (1.2) для нашего примера. В табл. 1.4 имеется 5 строк и 2 столбца, следовательно, сумма рангов будет равна
((5-2 + 1) — 5 — 2)/2 = 55.
Ранжирование по cm рокам
Пример 1.4. В предыдущем примере 1.3 добавили еще одну группу испытуемых из 5 человек. Получится табл. 1.5, в которой проведем ранжирование но строчкам.
Получится табл. 1.5, в которой проведем ранжирование но строчкам.
Суммы по столбцам
Обратите внимание, что в табл. 1.5 минимальному по величине числу ставится минимальный ранг, хотя можно было бы сделать и наоборот.
В любом случае сумма всех рангов но каждой строчке должна быть равна 6, поскольку у нас ранжируется всего три величины: 1 + 2 + 3 = 6.В нашем случае так оно и есть. Теперь просуммируем ранги по каждому столбцу отдельно и сложим их.
Расчетная формула общей суммы рангов для ранжирования по строчкам для таблицы определяется по формуле:
где п — количество испытуемых в столбце; с — количество столбцов (групп).
Правильность ранжирования вновь определяется условием совпадения расчетных сумм реальных рангов, полученных при подсчете в таблице и по расчетной формуле (1.3).
Проверим правильность ранжирования для нашего примера.
Реальная сумма рангов в таблице: 8 + 10 + 12 = 30.
По формуле (1.3): 5-3-(3 + 1)/2 = 30.
Следовательно, ранжирование было проведено правильно.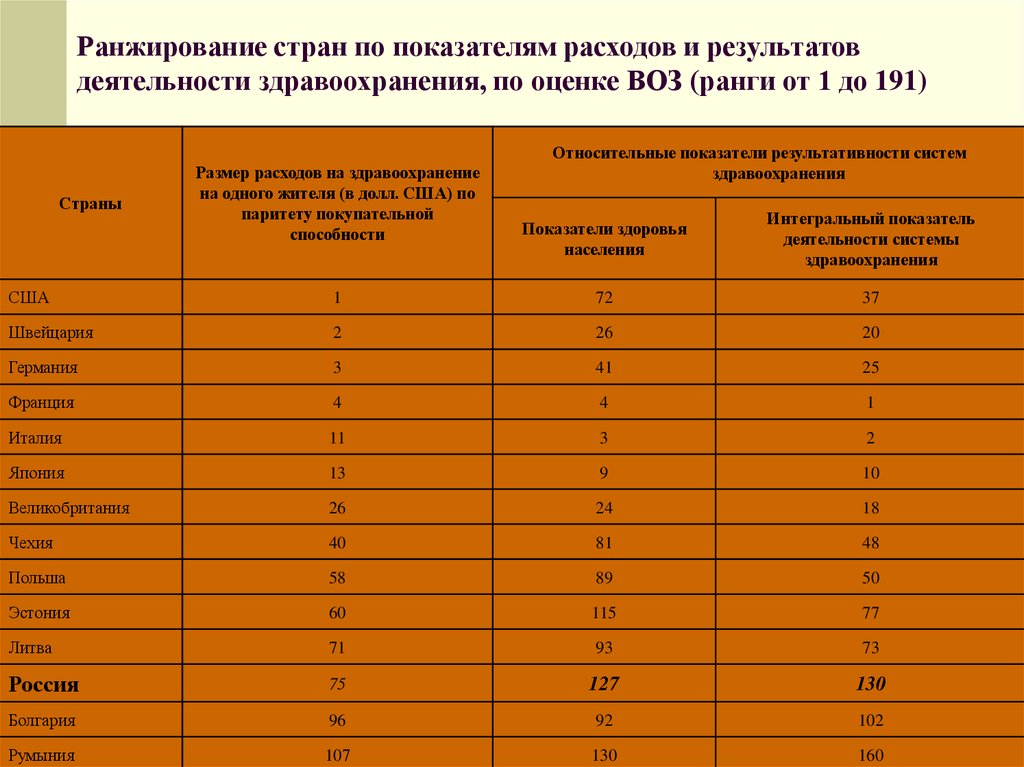
Ранговая статистика — Математическая энциклопедия
Статистика (см. Статистическая оценка), построенная из рангового вектора. Если $ R = ( R _ {1} \dots R _ {n} ) $
вектор рангов, построенный из случайного вектора наблюдений $ X = ( X _ {1} \dots X _ {n} ) $,
то любая статистика $T = T(R)$
которая является функцией $ R $
называется ранговой статистикой. Классическим примером ранговой статистики является коэффициент Кендалла ранговой корреляции $\tau$
между векторами $R$
и $ \ell = ( 1 \dots n ) $,
определяется по формуле
9{ п }
\влево ( я — п+
\фракция{1}{2}
\правильно )
\left ( R _ {i} — n+
\фракция{1}{2}
\правильно ) ,
$$
— линейная ранговая статистика.
Линейные ранговые статистики, как правило, просто построить с вычислительной точки зрения и их распределения легко найти. По этой причине понятие проектирования ранговой статистики в семейство линейных ранговых статистик играет важную роль в теории ранговой статистики. Если $Т$
представляет собой ранговую статистику, построенную из случайного вектора $ X $
при гипотезе $ H _ {0} $
о его распределении, то линейная ранговая статистика $ \widehat{T} = \widehat{T} ( R) $
такой, что $ {\mathsf E} \{ ( T — \widehat{T} ) ^ {2} \} $
минимальна при условии, что $ H _ {0} $
верно, называется проекцией $T$
в семейство линейных ранговых статистик.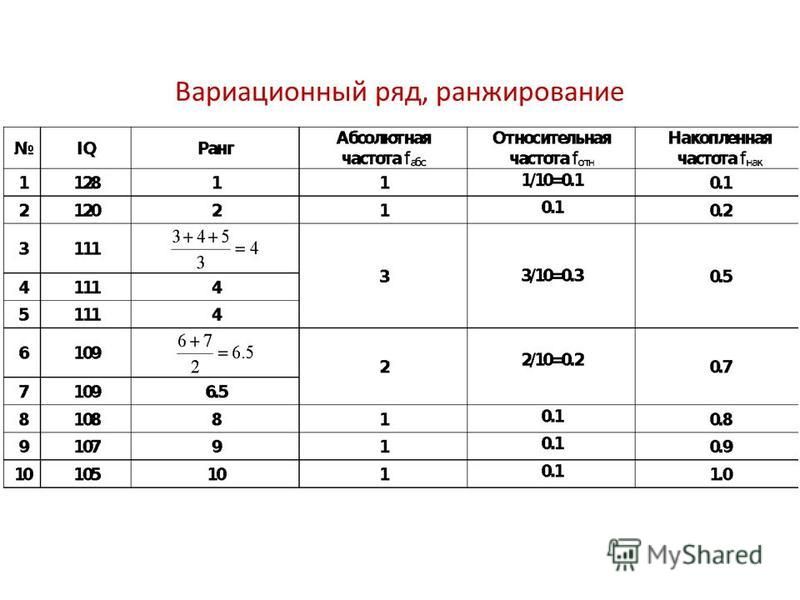 Как правило, $ \widehat{T} $
Как правило, $ \widehat{T} $
приближается к $ T $
ну и разница $ T — \widehat{T} $
пренебрежимо мал как $ n \rightarrow \infty $.
Если гипотеза $ H _ {0} $
при котором компоненты $ X _ {1} \dots X _ {n} $
случайного вектора $ X $
являются независимыми случайными величинами, то проекция $ \widehat{T} $
$ Т $
можно определить по формуле
9{ п }
\ widehat {a} ( я , р _ {я} ) — ( п — 2 ) {\ mathsf E} \ {T \},
$$
где $ \widehat{a} ( i , j ) = {\mathsf E} \{T \mid R _ {i} = j \}$,
$ 1 \leq i , j \leq n $
(см. [1]).
Существует внутренняя связь между $ \tau $
и $\ро$.
В [1] показано, что проекция $ \widehat \tau $
коэффициента Кендалла $\tau$
в семейство линейных ранговых статистик совпадает с точностью до мультипликативной константы с коэффициентом Спирмена $\rho$;
а именно,
$$
\широкая шляпа\тау =
\фракция{2}{3}
\влево ( 1 +
\фракция{1}{п}
\справа ) \ро .
$$
Из этого равенства следует, что коэффициент корреляции $ \mathop{\rm corr} ( \rho , \tau ) $
между $\rho$
и $\тау$
равно
$$
\mathop{\rm корр} ( \rho , \tau ) = \
\ кв {
\ frac { {\ mathsf D} \ widehat \ tau }{ {\ mathsf D} \ tau}
знак равно
\ frac {2 ( п + 1 ) } {\ sqrt {2 п ( 2 п + 5 ) } }
,
$$
, из чего следует, что эти ранговые статистики асимптотически эквивалентны для больших $ n $(
ср. [2]).
[2]).
Литература
| [1] | Й. Хайек, З. Сидак, «Теория ранговых тестов», акад. Press (1967) |
| [2] | М.Г. Кендалл, «Методы ранговой корреляции», Гриффин (1970) |
Как процитировать эту запись:
Ранговая статистика. Математическая энциклопедия. URL: http://encyclopediaofmath.org/index.php?title=Rank_statistic&oldid=51568
Эта статья была адаптирована из оригинальной статьи М.С. Никулин (создатель), опубликованный в Математической энциклопедии — ISBN 140200609.8. См. исходную статью
2023 Лучшие школы статистики — College Factual
Степень в области статистики более популярна, чем многие другие степени. Фактически, он занимает 85-е место из 395 по популярности всех таких степеней в стране. В результате есть много колледжей, которые предлагают степень, что затрудняет выбор школы.
В 2023 году College Factual проанализировал 136 школ, чтобы определить лучшие из них для своего рейтинга лучших статистических школ. В совокупности эти школы раздали 9979 степеней по статистике для квалифицированных студентов.
Перейти к одному из следующих разделов: * Рейтинги степеней
- Список лучших школ по общей статистике
Ваш выбор статистической школы имеет значение, поэтому мы составили этот рейтинг, чтобы помочь вам принять решение. Мы получаем наш рейтинг лучших школ общей статистики путем свертки наших рейтингов по уровням после взвешивания их по количеству степеней, присуждаемых в каждой школе.
Вы можете выбрать один из указанных ниже уровней образования, чтобы найти наиболее интересующие вас учебные заведения.
Выберите свой уровень статистики
Школа статистики, которую вы выбираете, чтобы вкладывать свое время и деньги в дела. Чтобы помочь вам принять правильное решение, мы разработали ряд рейтингов по основным направлениям, в том числе этот список лучших школ статистики.
Если вы хотите ограничить свой выбор только одной частью страны, вы можете отфильтровать этот список по местоположению.
В дополнение к нашему рейтингу вы можете выбрать два колледжа и сравнить их по наиболее важным для вас критериям в нашем уникальном инструменте College Combat.
Проверьте это, когда у вас есть шанс! Вы также можете добавить ссылку в закладки и поделиться ею с другими, кто пытается принять решение о поступлении в колледж.
Если вы хотите узнать больше о том, как мы получаем наши рейтинги, см. Методологию College Factual.
Избранные статистические программы
Узнайте о датах начала, переносе кредитов, доступности финансовой помощи и многом другом, связавшись с университетами, указанными ниже.
РЕКЛАМА
| Посетите сайт | Бакалавр математики Если у вас есть способности к математике и вы хотите узнать больше, учитесь онлайн, чтобы достичь своих карьерных целей в Университете Южного Нью-Гэмпшира. |
| Посетите сайт | Бакалавр математики — прикладная математика Примените математические концепции для решения самых сложных современных реальных задач, изучая прикладную математику с этим специализированным онлайн-курсом бакалавра из Университета Южного Нью-Гэмпшира. |
Хотя мы рекомендуем сначала отфильтровать по уровню степени, вы можете просмотреть список ниже, чтобы увидеть, какие школы предоставляют образовательный опыт для предлагаемых ими уровней степени статистики. Только те школы, которые занимают 9-е место.0052 лучшие 15% из всех школ, которые мы проанализировали, получили место в этом списке.
20 лучших школ по статистике
#1
Чикагский университет
Чикаго, Иллинойс
Чикагский университет — отличный выбор для студентов, изучающих статистику. Расположенный в городе Чикаго, UChicago является частным некоммерческим университетом с довольно большим количеством студентов. 7-е место в рейтинге лучших колледжей из 2241 школы по всей стране означает, что UChicago в целом является отличным университетом.
Расположенный в городе Чикаго, UChicago является частным некоммерческим университетом с довольно большим количеством студентов. 7-е место в рейтинге лучших колледжей из 2241 школы по всей стране означает, что UChicago в целом является отличным университетом.
Примерно 283 студента-статистика получили эту степень в Калифорнийском университете в Чикаго за последний год, по которому у нас есть данные. Те студенты статистики, которые получают степень в Чикагском университете, зарабатывают на 57 403 доллара больше, чем обычные выпускники статистики.
Дополнительная информация о степени по статистике Чикагского университета. Карнеги-Меллон, расположенный в городе Питтсбург, является частным некоммерческим университетом с большим количеством студентов. 8-е место в рейтинге лучших колледжей из 2241 школы по всей стране означает, что Карнеги-Меллон в целом является отличным университетом.
Около 225 студентов-статистиков получили эту степень в Карнеги-Меллон за последний год, по которому мы располагаем данными. Получатели степени в области статистики Университета Карнеги-Меллона зарабатывают примерно на 25 793 доллара больше, чем обычные заработки специалистов по статистике.
Получатели степени в области статистики Университета Карнеги-Меллона зарабатывают примерно на 25 793 доллара больше, чем обычные заработки специалистов по статистике.
Дополнительная информация о степени по статистике в Университете Карнеги-Меллона
#3
Корнельский университет
Итака, штат Нью-Йорк
Любой студент, стремящийся получить степень в области статистики, должен заглянуть в Корнельский университет. Корнелл — довольно крупный частный некоммерческий университет, расположенный в городе Итака. 13-е место в рейтинге лучших колледжей из 2241 колледжа по всей стране означает, что Корнелл в целом является отличным университетом.
Около 97 студентов-статистиков получили эту степень в Корнеллском университете за последний отчетный год. Получатели степени по программе статистической степени в Корнельском университете получают на 21 325 долларов больше, чем типичный выпускник колледжа с той же степенью, когда они поступают на работу.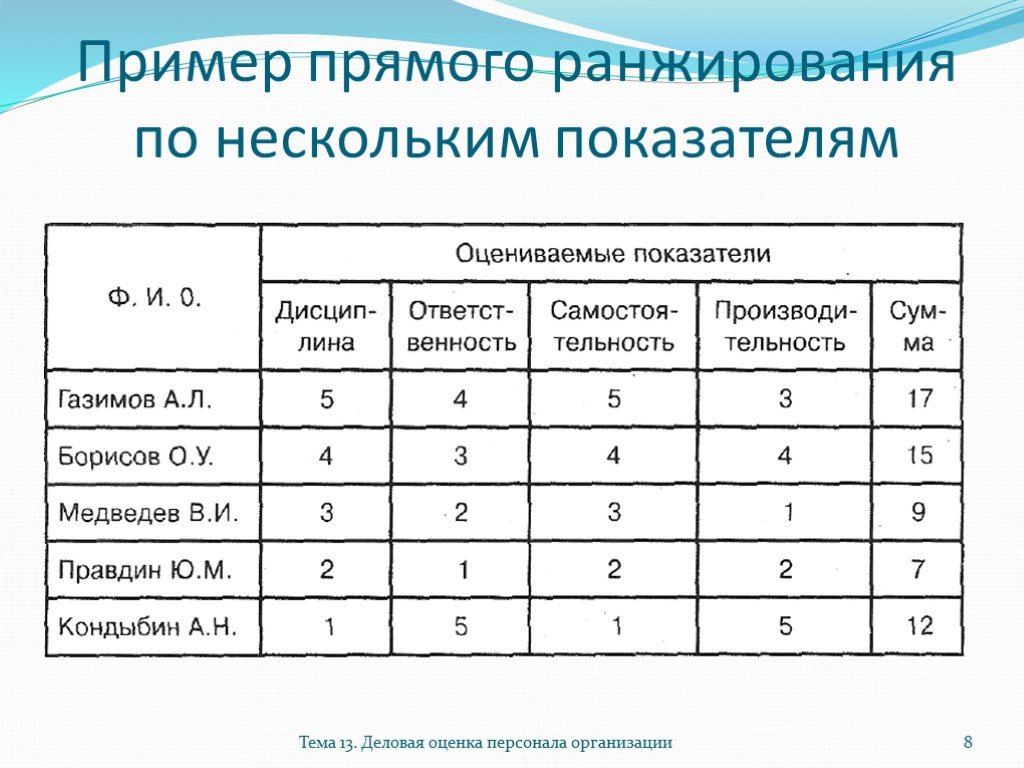
Дополнительная информация о степени по статистике в Корнельском университете
#4
Университет Джона Хопкинса
Балтимор, Мэриленд
Университет Джона Хопкинса – одна из лучших школ в стране для получения степени в области статистики. Johns Hopkins — очень крупный частный некоммерческий университет, расположенный в большом городе Балтимор. 9 место в рейтинге лучших колледжейиз 2241 колледжа по всей стране означает, что Джонс Хопкинс в целом является отличным университетом.
Около 37 студентов-статистиков получили эту степень в Университете Джонса Хопкинса за последний отчетный год.
Дополнительная информация о степени по статистике Университета Джона Хопкинса
#5
Университет Эмори
Атланта, Джорджия
Частный некоммерческий университет Эмори, расположенный в большом городе Атланта, в котором учится много студентов численность населения.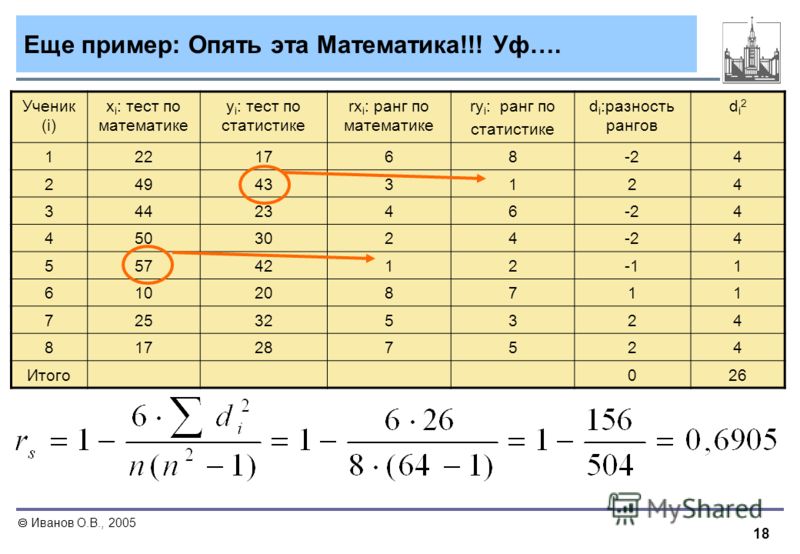 Этот университет занимает 2-е место из 69школы общего качества в штате Джорджия.
Этот университет занимает 2-е место из 69школы общего качества в штате Джорджия.
Около 113 студентов-статистиков получили эту степень в Эмори за последний год, по которому у нас есть данные. Те студенты статистики, которые получают степень в Университете Эмори, получают на 4108 долларов больше, чем обычные выпускники статистики.
Дополнительная информация о степени по статистике Университета Эмори
#6
Колумбийский университет в городе Нью-Йорк
Нью-Йорк, штат Нью-Йорк
Расположенный в большом городе Нью-Йорк, Колумбия является частным некоммерческим университетом с довольно большим количеством студентов. 14-е место в рейтинге лучших колледжей из 2241 колледжа по всей стране означает, что Колумбия в целом является отличным университетом.
Около 651 студента-статистика окончили Колумбийский университет с этой степенью за последний отчетный год. Те студенты статистики, которые получают степень в Колумбийском университете в городе Нью-Йорк, зарабатывают на 30 246 долларов больше, чем обычные выпускники статистики.
Дополнительная информация о степени по статистике Колумбийского университета в городе Нью-Йорк
#7
Гарвардский университет
Кембридж, Массачусетс
Гарвард — очень крупный частный некоммерческий университет, расположенный в городе среднего размера. Кембриджа. 12-е место в рейтинге лучших колледжей среди 2241 колледжа по всей стране означает, что Гарвард в целом является отличным университетом.
Примерно 73 студента-статистика получили эту степень в Гарварде за последний отчетный год. Получатели степени по специальности статистика в Гарвардском университете получают на 16 180 долларов больше, чем средний выпускник колледжа в этой области, когда они поступают на работу.
Дополнительная информация о степени Гарвардского университета по статистике
#8
Нью-Йоркский университет
Нью-Йорк, штат Нью-Йорк
Расположенный в городе Нью-Йорк, Нью-Йоркский университет является частным некоммерческим университетом с очень большой студенческий контингент. Этот университет занимает 3-е место из 143 школ по общему качеству в штате Нью-Йорк.
Этот университет занимает 3-е место из 143 школ по общему качеству в штате Нью-Йорк.
Около 180 студентов-статистиков окончили Нью-Йоркский университет с этой степенью за последний отчетный год. Получатели степени в области статистики из Нью-Йоркского университета зарабатывают около 47,9 долларов США.13 выше типичных заработков выпускников-статистиков.
Дополнительная информация о степени по статистике Нью-Йоркского университета
#9
Калифорнийский университет — Лос-Анджелес
Лос-Анджелес, Калифорния
Расположенный в городе Лос-Анджелес, UCLA является государственным университетом с довольно большой студенческое население. Этот университет занимает 6-е место из 170 школ по общему качеству в штате Калифорния.
Около 236 студентов-статистиков получили эту степень в Калифорнийском университете в Лос-Анджелесе за последний отчетный год. Студенты, получившие степень по программе статистики, зарабатывают около 56 134 долларов в первые пару лет работы.
Дополнительная информация о степени по статистике Калифорнийского университета в Лос-Анджелесе. 17-е место в рейтинге лучших колледжей из 2241 колледжа по всей стране означает, что Калифорнийский университет в Беркли в целом является отличным университетом.
Около 197 студентов-статистиков получили эту степень в Калифорнийском университете в Беркли за последний год, по которому у нас есть данные. Те студенты статистики, которые получают степень в Калифорнийском университете в Беркли, зарабатывают на 8 214 долларов больше, чем обычные выпускники статистики.
Дополнительная информация о степени по статистике Калифорнийского университета в Беркли
#11
Северо-Западный университет
Эванстон, Иллинойс
Северо-Западный университет — довольно крупный частный некоммерческий университет, расположенный в городе Эванстон. 5-е место среди лучших колледжей среди 2241 школы по всей стране означает, что Северо-Западный университет в целом является отличным университетом.
Около 66 студентов-статистиков получили эту степень в Северо-Западном университете за последний год, по которому мы располагаем данными. Студенты, окончившие программу статистики со степенью, сообщают, что средний заработок в начале карьеры составляет 59 долларов.,892.
Дополнительная информация о степени по статистике Северо-Западного университета
#12
Иллинойсский университет в Урбана-Шампейн
Шампейн, Иллинойс
Государственный университет UIUC, расположенный в небольшом городе Шампейн, в котором учится очень много студентов численность населения. Этот университет занимает 3-е место из 87 школ по общему качеству в штате Иллинойс.
Около 518 студентов-статистиков окончили UIUC с этой степенью в последнем отчетном году. Получатели степени по статистике из Университета Иллинойса в Урбана-Шампейн зарабатывают примерно 12 879 долларов США.выше среднего дохода специалистов по статистике.
Более подробная информация о степени по статистике Университета Иллинойса в Урбана-Шампейн
#13
Университет Пердью – главный кампус
Вест-Лафайет, Индиана
Purdue – очень крупный государственный университет, расположенный в городе Уэст-Лафайет. . Этот университет занимает 2-е место из 42 колледжей по общему качеству в штате Индиана.
. Этот университет занимает 2-е место из 42 колледжей по общему качеству в штате Индиана.
Примерно 262 студента-статистика получили эту степень в Purdue за последний год, по которому у нас есть данные. Получатели степени по программе статистики в Университете Пердью — главный кампус зарабатывают на 6 728 долларов больше, чем типичный выпускник с той же степенью вскоре после выпуска.
Более подробная информация о степени по статистике Университета Пердью — главный кампус
#14
Южный методистский университет
Даллас, Техас
Расположенный в большом пригороде Далласа, SMU является частным некоммерческим университетом с достаточно большой контингент учащихся. Этот университет занимает 4-е место из 116 школ по общему качеству в штате Техас.
Около 98 студентов-статистиков закончили SMU с этой степенью в последний год, по которому у нас есть данные.
Более подробная информация о степени по статистике Южного методистского университета
#15
Дартмутский колледж
Ганновер, Нью-Гемпшир
Дартмут — это небольшой частный некоммерческий колледж, расположенный в отдаленном городе Ганновер. 22-е место в рейтинге лучших колледжей среди 2241 колледжа по всей стране означает, что Дартмут в целом является отличным колледжем.
22-е место в рейтинге лучших колледжей среди 2241 колледжа по всей стране означает, что Дартмут в целом является отличным колледжем.
Примерно 6 студентов-статистиков получили эту степень в Дартмуте за последний год, по которому у нас есть данные.
Дополнительная информация о степени по статистике Дартмутского колледжа
#16
Вашингтонский университет в Сент-Луисе
Сент-Луис, Миссури
Расположенный в пригороде Сент-Луиса, WUSTL является частным некоммерческим университетом с большой студенческий контингент. 24-е место в рейтинге лучших колледжей из 2241 школы по всей стране означает, что WUSTL в целом является отличным университетом.
Около 17 студентов-статистиков получили эту степень в WUSTL за последний отчетный год.
Дополнительная информация о степени по статистике Вашингтонского университета в Сент-Луисе
#17
Университет Джорджа Вашингтона
Вашингтон, округ Колумбия
GWU — очень крупный частный некоммерческий университет, расположенный в городе Вашингтон. Этот университет занимает 2-е место из 8 колледжей по общему качеству в штате округ Колумбия.
Этот университет занимает 2-е место из 8 колледжей по общему качеству в штате округ Колумбия.
Около 123 студентов-статистиков получили эту степень в GWU за последний год, по которому у нас есть данные.
Дополнительная информация о степени по статистике Университета Джорджа Вашингтона
#18
Университет Нотр-Дам
Нотр-Дам, IN
Расположенный в пригороде Нотр-Дам, Нотр-Дам является частным некоммерческим университетом. с довольно большим контингентом учащихся. 16-е место в рейтинге лучших колледжей из 2241 колледжа по всей стране означает, что Нотр-Дам в целом является отличным университетом.
Около 8 студентов-статистиков получили эту степень в Нотр-Даме за последний отчетный год.
Более подробная информация о степени по статистике Университета Нотр-Дам
#19
Университет Висконсина — Мэдисон
Мэдисон, Висконсин
Расположенный в городе Мэдисон, штат Вашингтон. Мэдисон является государственным университетом с довольно большим студенческое население. Этот университет занимает 1-е место из 46 школ по общему качеству в штате Висконсин.
Мэдисон является государственным университетом с довольно большим студенческое население. Этот университет занимает 1-е место из 46 школ по общему качеству в штате Висконсин.
Около 210 студентов-статистиков получили эту степень в Университете Вашингтона в Мэдисоне за последний год, по которому мы располагаем данными.
Более подробная информация о степени по статистике Университета Висконсина — Мэдисон
#20
Университет Мичигана — Анн-Арбор
Анн-Арбор, Мичиган
UM — довольно крупный государственный университет, расположенный в городе Анн-Арбор. 25-е место в рейтинге лучших колледжей из 2241 колледжа по всей стране означает, что UM в целом является отличным университетом.
Около 160 студентов-статистиков получили эту степень в Университете Массачусетса за последний год, по которому у нас есть данные. Студенты, окончившие программу статистики со степенью, заявляют, что их средний заработок в начале карьеры составляет 63 759 долларов. .
.
Дополнительная информация о степени по статистике Мичиганского университета в Анн-Арборе
Остальные лучшие школы статистики
Дополнительные заслуживающие внимания школы
Это некоторые дополнительные школы, заслуживающие упоминания, которые также замечательны, но не очень популярны. сокращение, чтобы заработать нашу высшую награду «Лучшие статистические школы».
| Должность | Колледж | Местоположение |
|---|---|---|
| 25 | Университет Вирджинии — главный кампус | Charlottesville, VA |
| 26 | University of California — Santa Barbara | Santa Barbara, CA |
| 27 | Brigham Young University — Provo | Provo, UT |
| 21 | Amherst College | Амхерст, Массачусетс |
| 22 | Техасский университет A&M – College Station | College Station, TX |
| 23 | Rochester, NY | |
| 24 | Williams College | Williamstown, MA |
| 25 | University of Virginia — Main Campus | Charlottesville, VA |
View the Best Statistics Schools for a specific регион рядом с вами.
| Регион |
|---|
| Юго-восток |
| Новая Англия |
| Скалистые горы |
| Plains States |
| Middle Atlantic |
| Far Western US |
| Southwest |
| Great Lakes |
Other Rankings
Master’s Degrees
in Stats
Best Value
по статистике
Лучший для нетрадиционных студентов
по статистике
Лучший онлайн
по статистике
Самый популярный онлайн
по статистике
Просмотреть все рейтинги >
Статистика — это один из 4 различных типов программ по математике и статистике на выбор.
Stats Focus Areas
| Major | Annual Graduates |
|---|---|
| Statistics | 8,503 |
| Other Statistics | 540 |
| Mathematical Statistics & Probability | 500 |
| Mathematics и статистика | 436 |
View All Stats Concentrations >
| Related Major | Annual Graduates |
|---|---|
| Mathematics | 30,202 |
| Applied Mathematics | 11,107 |
| Other Statistics | 644 |
| Прикладная статистика | 464 |
Посмотреть всю статистику Связанные специальности >
Примечания и ссылки
- Столбцы на диаграммах выше показывают распределение школ в этом списке +/- одно стандартное отклонение от среднего.


 Наша степень по математике может помочь вам улучшить свои математические способности, включая рассуждения и решение задач в трех областях: анализ, алгебра и статистика.
Наша степень по математике может помочь вам улучшить свои математические способности, включая рассуждения и решение задач в трех областях: анализ, алгебра и статистика.