Содержание
Коэффициент ранговой корреляции Спирмена онлайн
Примеры решенийКоэффициент СпирменаКоэффициент Кендалла
Коэффициент конкордацииКоэффициент контингенции
Группировка данных
Показатели вариации
Доверительный интервал
Различие средних
Коэффициент ранговой корреляции Спирмена — это количественная оценка статистического изучения связи между явлениями, используемая в непараметрических методах.
Показатель показывает, как отличается полученная при наблюдении сумма квадратов разностей между рангами от случая отсутствия связи.
Назначение сервиса. С помощью данного онлайн-калькулятора производится:
- расчет коэффициента ранговой корреляции Спирмена;
- вычисление доверительного интервала для коэффициента и оценка его значимости;
- Шаг №1
- Шаг №2
- Видеоинструкция
Инструкция.
Укажите количество данных (количество строк), нажмите Далее. Полученное решение сохраняется в файле Word (см пример нахождения коэффициента ранговой корреляции Спирмена). Также создается шаблон решения в Excel.
Количество строк
Коэффициент ранговой корреляции Спирмена относится к показателям оценки тесноты связи. Качественную характеристику тесноты связи коэффициента ранговой корреляции, как и других коэффициентов корреляции, можно оценить по шкале Чеддока.
Расчет коэффициента состоит из следующих этапов:
- Ранжирование признаков по возрастанию. Ранг – это порядковый номер. Если встречаются два одинаковых значения, им присваивают одинаковое значение ранга, равное среднему арифметическому рангов этих значений.
- Определение разности рангов каждой пары сопоставляемых значений, d = dx — dy.
- Возведение в квадрат разность di и нахождение общей суммы, ∑d2.
- Вычисление коэффициента корреляции рангов по формуле:
где d2 – квадратов разностей между рангами; N – количество признаков, участвовавших в ранжировании.
Свойства коэффициента ранговой корреляции Спирмена
- Нормируемость. Коэффициент корреляции рангов может принимать значения от -1 до +1.
p = 1свидетельствует о возможном наличии прямой связи,p =-1свидетельствует о возможном наличии обратной связи. - Ограниченность. Для оценки данных необходима выборка от 5 до 40 наблюдений по каждой переменной. При большом количестве одинаковых рангов по сопоставляемым переменным коэффициент дает приближенные значения. При совпадении значений вносится поправка на одинаковые ранги. В этом случае формула имеет вид:
где d2 – квадратов разностей между рангами; Тa, Тb – поправки на одинаковые ранги; N – количество признаков, участвовавших в ранжировании.
- Независимость. Чтобы получить адекватный результат, необязательно наличие нормального закона распределения коррелируемых рядов.
Область применения. Коэффициент корреляции рангов используется для оценки качества связи между двумя совокупностями. Кроме этого, его статистическая значимость применяется при анализе данных на гетероскедастичность.
Пример. По выборке данных наблюдаемых переменных X и Y:
- составить ранговую таблицу;
- найти коэффициент ранговой корреляции Спирмена и проверить его значимость на уровне 2a
- оценить характер зависимости
Решение. Присвоим ранги признаку Y и фактору X.
| X | Y | ранг X, dx | ранг Y, dy |
| 28 | 21 | 1 | 1 |
| 30 | 25 | 2 | 2 |
| 36 | 29 | 4 | 3 |
| 40 | 31 | 5 | 4 |
| 30 | 32 | 3 | 5 |
| 46 | 34 | 6 | 6 |
| 56 | 35 | 8 | 7 |
| 54 | 38 | 7 | 8 |
| 60 | 39 | 10 | 9 |
| 56 | 41 | 9 | 10 |
| 60 | 42 | 11 | 11 |
| 68 | 44 | 12 | 12 |
| 70 | 46 | 13 | 13 |
| 76 | 50 | 14 | 14 |
Матрица рангов.
| ранг X, dx | ранг Y, dy | (dx — dy)2 |
| 1 | 1 | 0 |
| 2 | 2 | 0 |
| 4 | 3 | 1 |
| 5 | 4 | 1 |
| 3 | 5 | 4 |
| 6 | 6 | 0 |
| 8 | 7 | 1 |
| 7 | 8 | 1 |
| 10 | 9 | 1 |
| 9 | 10 | 1 |
| 11 | 11 | 0 |
| 12 | 12 | 0 |
| 13 | 13 | 0 |
| 14 | 14 | 0 |
| 105 | 105 | 10 |
Проверка правильности составления матрицы на основе исчисления контрольной суммы:
Сумма по столбцам матрицы равны между собой и контрольной суммы, значит, матрица составлена правильно.
По формуле вычислим коэффициент ранговой корреляции Спирмена.
Связь между признаком Y и фактором X сильная и прямая
Значимость коэффициента ранговой корреляции Спирмена
Для того чтобы при уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента ранговой корреляции Спирмена при конкурирующей гипотезе Hi. p ≠ 0, надо вычислить критическую точку:
где n — объем выборки; ρ — выборочный коэффициент ранговой корреляции Спирмена: t(α, к) — критическая точка двусторонней критической области, которую находят по таблице критических точек распределения Стьюдента, по уровню значимости α и числу степеней свободы k = n-2.
Если |p| < Тkp — нет оснований отвергнуть нулевую гипотезу. Ранговая корреляционная связь между качественными признаками не значима. Если |p| > Tkp — нулевую гипотезу отвергают. Между качественными признаками существует значимая ранговая корреляционная связь.
По таблице Стьюдента находим t(α/2, k) = (0.1/2;12) = 1.782
Поскольку Tkp < ρ, то отклоняем гипотезу о равенстве 0 коэффициента ранговой корреляции Спирмена. Другими словами, коэффициент ранговой корреляции статистически — значим и ранговая корреляционная связь между оценками по двум тестам значимая.
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
ноль интерактивности и ужасный монтаж видео
Курс точно не стоит своих денег. Особенно после отмены очных сессий и с таким качеством монтажа. Как часто бывает с материалами по ML, все лучшие курсы, учебные материалы и статьи вы найдете в открытом доступе бесплатно. Я бы мог посоветовать модуль по АБ-тестам, он реально хорош.
Достоинства
Четвертый модуль по АБ-тестам — это лучшее, что я видел по данной тематике вне зависимости от языка учебного материала.
Превосходный учитель, большой специалист и харизматичный человек.
Интересная подача, каждый слайд разбирается досконально: с выводом формул, подробным описанием и практическим применением. Таким образом, к концу лекции ты получаешь не просто готовый ответ «sample size считается вот так», а понимаешь каждый шаг, который привел к такому результату. Если бы я оценивал только четвертый модуль, то поставил бы 5+.
Недостатки
1. Ужасный монтаж видео. Ну, правда, возьмите и запишите видео заново, а не делайте пять склеек в одном предложении: «и поэтому | модель | должна будет | вернуть предсказанную | вероятность». Я не утрирую, просто откройте хотя бы модуль «ценообразование» и убедитесь сами.
2. Далее про сам модуль ценообразования: неструктурированный набор лекций, не создается целостной картины «а изучаем-то чего?». Сначала тратится три лекции на элементарный препроцессинг (хотя в описании курса HARD ML написано для уровней senior DS), потом идет элементарная регрессия (простая и квантильная), «галопом по Европам» временные модели и.
..многорукие бандиты. Новых знаний с модуля получаешь крайне мало. Куда лучше было бы разобрать более глубоко какую-то подобласть в ценообразовании, чем пытаться объять необъятное.
3. Ранжирование и матчинг. Первое и главное — довольно токсичный преподаватель. На ранних запусках курса, когда были очные сессии, на уточняющий вопрос по теории или ДЗ я часто сталкивался с ответом преподавателя: «перечитайте внимательнее, в описании все есть».
Уважаемый преподаватель, вы составляете учебный материал, разумеется, для вас там вопросов нет и все очевидно. Но если из раза в раз, чтобы получить ответ на вопрос, приходится читать между строк, то, возможно, для студентов не все так очевидно. На n-ом этапе я просто перестал спрашивать, если не мог найти ответ самостоятельно, то ждал разбора ДЗ. Всяко лучше, чем тратить нервы на токсичное общение.
Касательно материала: на самом деле довольно неплохой курс, очень много приходится писать с нуля, что здорово. Сильно прокачался в PyTorch из-за этого.
Из минусов по материалам: мы, вроде, ранжирование и матчинг проходим, зачем в последних лекциях делать больший упор на эмбеддинги, Bert и трансформеры, если мы не используем их ни в одном из ДЗ, ни в финальном проекте. Вместо этого можно было бы разобрать sota в ранжирование, а не заканчивать на реализации KNRM.
4. Ребята с четвертого запуска курса убрали очные сессии с преподавателями по ДЗ. Раньше ты мог голосом обсудить свои вопросы, задать вопрос по коду и получить ответ. Это нормальный процесс взаимодействия преподавателя и студента. Именно за это я и готов платить 150к за курс! Но, видимо, такие сессии решили упразднить из-за высокой трудоемкости, оставив лишь видеообзоры домашки.
Ноль интерактивности — это большое упущение. Да, есть возможность спросить преподавателя в slack, но он не уделит тебе столько времени и не разберет проблему так досконально, как это было на очных сессиях. К тому же время ответа занимало несколько дней, а несколько вопросов по модулю АБ-тестов остались без ответов (организаторы могут поднять переписку в slack и убедиться в моих словах).
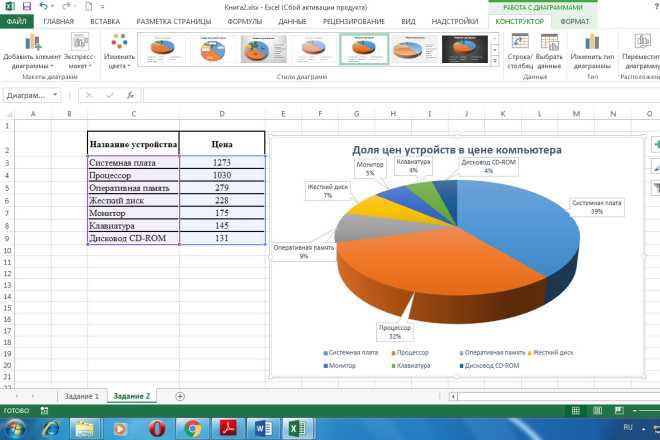
Новости CQG | Динамическое ранжирование в Excel
В этой статье рассматриваются подробности использования трех функций Microsoft Excel®: РАНГ, СЧЁТЕСЛИ и ВПР. Эти функции используются для создания информационной панели Excel, которая автоматически ранжирует набор рынков на основе процентного чистого изменения, а затем отображает рыночные символы, ранжированные от первого до последнего в столбце. Предоставляется загружаемый образец Excel.
Преимущество динамического ранжирования группы рынков по чистому процентному изменению заключается в том, что это позволяет трейдеру просто увидеть сильные и слабые стороны без необходимости сравнивать значения от ячейки к ячейке.
Excel предлагает функцию ранжирования, с помощью которой вы можете увидеть, где находится значение в одной ячейке в ранжированном порядке набора ячеек в столбце. Ниже в столбце A приведены примеры символов для пяти рынков, в столбце B указаны чистые процентные изменения для пяти рынков в ячейках с B1 по B5.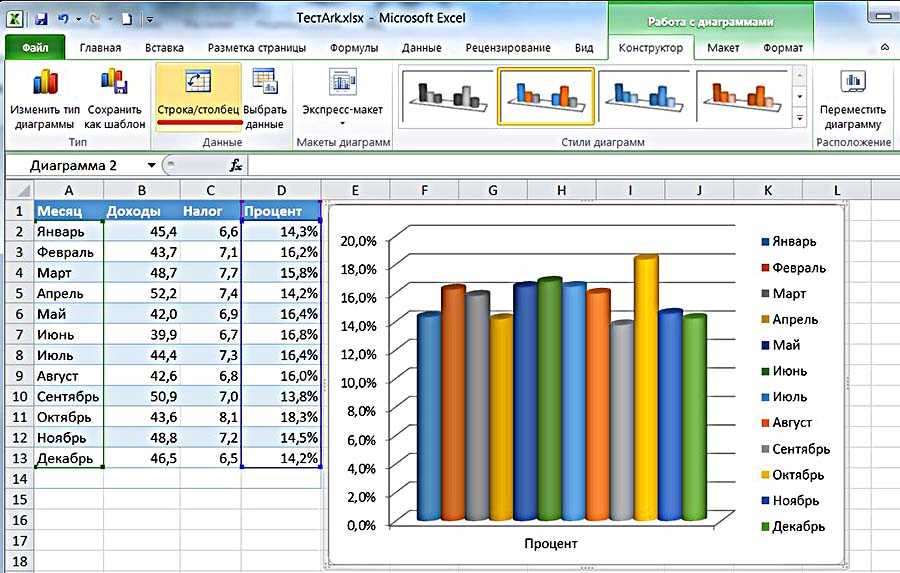
Функция ранга в ячейке C1 будет выглядеть так:
=РАНГ(B1,$B$1:$B$5,0)
Вы копируете и вставляете эту формулу в ячейку C1 до ячейки C5. Показанная выше функция Rank проверяет порядок ранжирования ячейки B1 в контрольном диапазоне от $B$1 до $B$5. Использование знаков доллара всегда блокирует диапазон от B1 до B5 при копировании и вставке. «0» означает, что результаты расположены в порядке возрастания, т. е. первый, второй, третий и т. д. Используйте «1», если вы хотите, чтобы результаты были в порядке убывания. В столбце C отображается ранг:
| А | Б | С | |
| 1 | А | 0,12% | 5 |
| 2 | Б | 0,55% | 1 |
| 3 | С | 0,12% | 4 |
| 4 | Д | 0,31% | 3 |
| 5 | Е | 0,44% | 2 |
Однако функция ранжирования Excel присваивает связи с одинаковым значением, как показано ниже с обновленными чистыми процентными изменениями для символов C и D.
Теперь оба отображают ранг 3 в столбце C:
| А | Б | С | |
| 1 | А | 0,12% | 5 |
| 2 | Б | 0,55% | 1 |
| 3 | С | 0,31% | 3 |
| 4 | Д | 0,31% | 3 |
| 5 | Е | 0,44% | 2 |
Во многих случаях ничья, присвоенная одному и тому же значению, не является проблемой. Здесь мы будем использовать ВПР, и если есть ничья, то это проблема, так как ВПР выдаст ошибку. Однако при использовании дополнительной функции СЧЁТЕСЛИ с функцией РАНГ ничьим автоматически будет присвоено следующее значение в ранге порядка. Ниже представлена функция СЧЁТЕСЛИ:
СЧЁТЕСЛИ($B$1:B1,B1)
Здесь СЧЁТЕСЛИ ищет в диапазоне от B1 до B1 и сколько раз встречается значение из ячейки B1.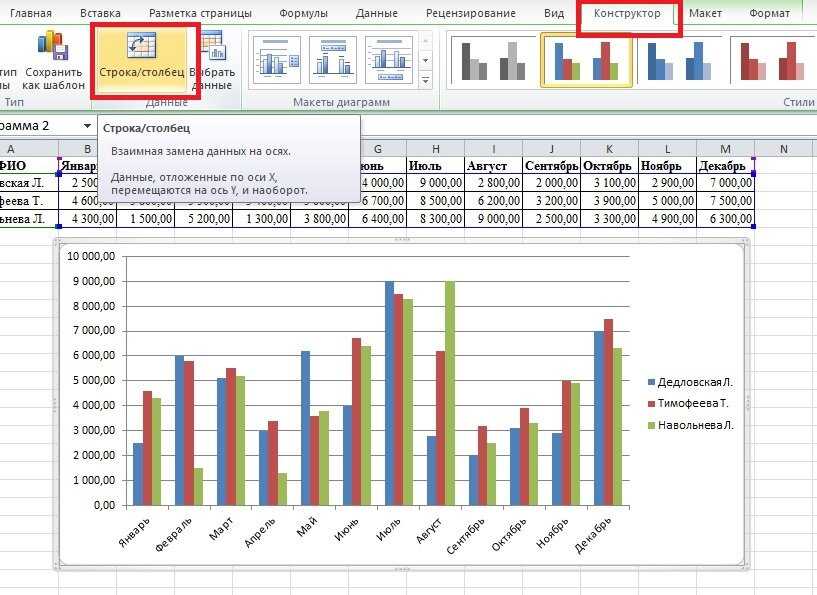
Очевидно, что значение в B1 может появиться только один раз в диапазоне от B1 до B1. Обратите внимание, знак доллара используется только в первой части диапазона. Когда эта формула копируется и вставляется вниз, то начало диапазона всегда равно B1, но нижняя часть диапазона будет зависеть от того, насколько глубоко копируются и вставляются формулы. В нашем примере будет использоваться диапазон до ячейки B5: 9.0003
СЧЁТЕСЛИ($B$1:B5,B5)
Вот модифицированная версия функции ранжирования, которая включает СЧЁТЕСЛИ и вводится в ячейку C1, копируется и вставляется в ячейку C5 (любезно предоставлено сайтом Чипа Пирсона):
=РАНГ(B1,$B$1:$B$5,0)+СЧЁТЕСЛИ($B$1:B1,B1)-1
СЧЁТЕСЛИ проверяет, сколько раз значение встречается в диапазоне. В нашем примере 0,31% встречается дважды. Итак, СЧЁТЕСЛИ вернёт два, а один вычтется из двух и прибавится к функции РАНГ. Этот дополнительный шаг устраняет ничьи:
| А | Б | С | |
| 1 | А | 0,12% | 5 |
| 2 | Б | 0,55% | 1 |
| 3 | С | 0,31% | 3 |
| 4 | Д | 0,31% | 4 |
| 5 | Е | 0,44% | 2 |
Мы видим, что в первый раз, когда встречается 0,31%, его ранг равен трем, а во второй раз — четырем.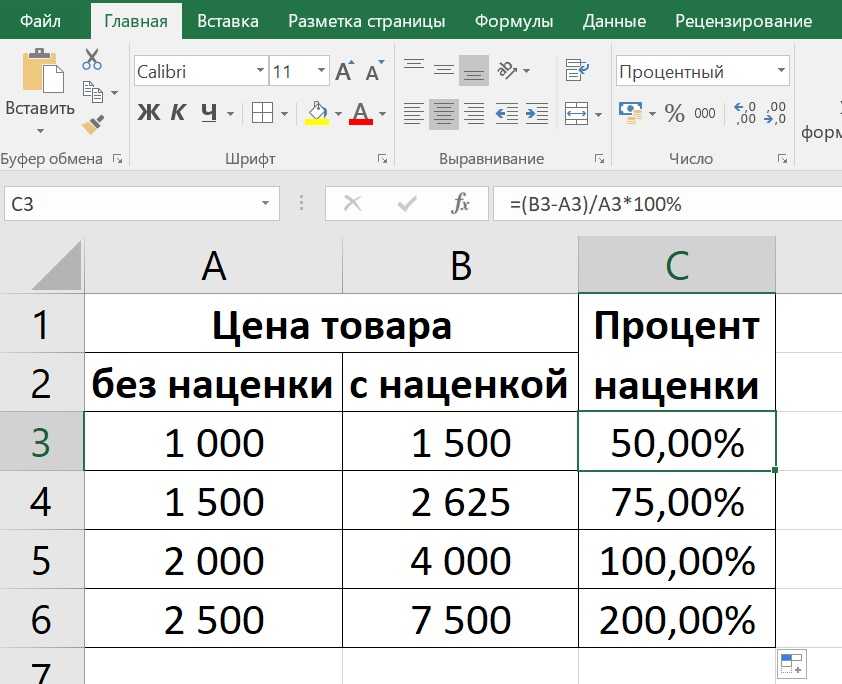
Давайте добавим символы рядом с рейтингом в столбце D и целые числа от 1 до 5 в столбце E, а затем воспользуемся функцией ВПР:
| А | Б | С | Д | Е | |
| 1 | А | 0,12% | 5 | А | 1 |
| 2 | Б | 0,55% | 1 | Б | 2 |
| 3 | С | 0,31% | 3 | С | 3 |
| 4 | Д | 0,31% | 4 | Д | 4 |
| 5 | Е | 0,44% | 2 | Е | 5 |
В столбце F используется функция ВПР. ВПР находит значение в диапазоне (столбце), а затем может вернуть информацию, которая находится рядом со значением в диапазоне.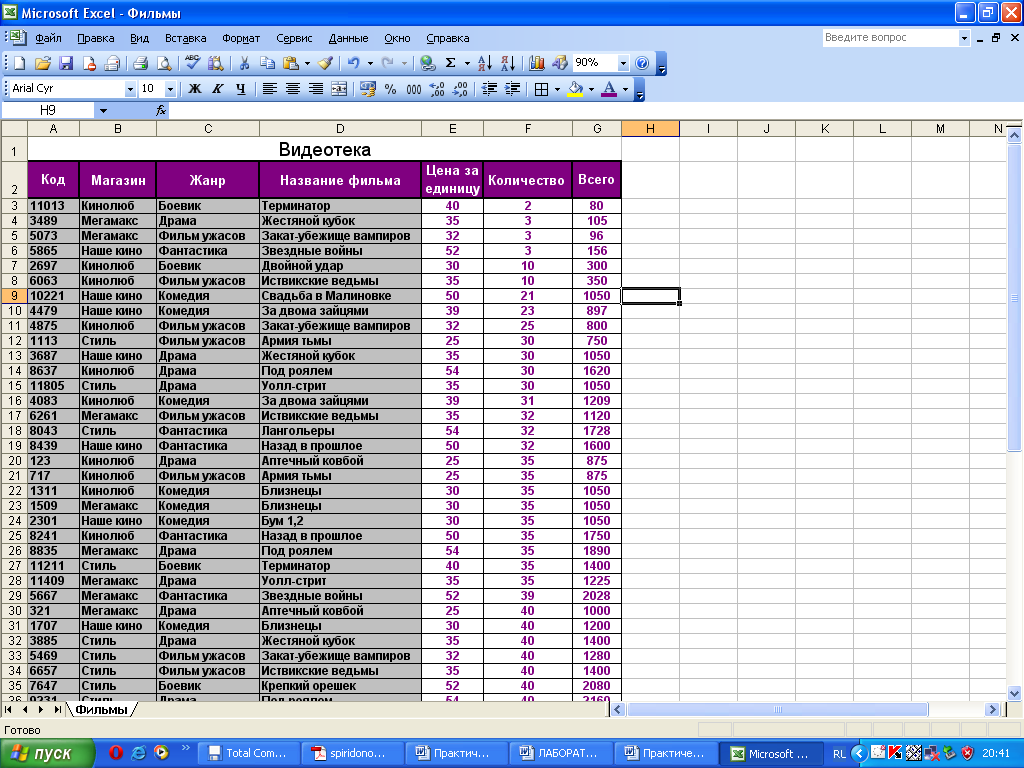
В ячейке F1 у нас есть:
=ВПР(E1,$C$1:$D$5,2,ЛОЖЬ)
Excel ищет значение в ячейке E1 в диапазоне от C1 до D5. Каждый столбец имеет значение индекса. Столбец C — это значение индекса 1, а столбец D — значение индекса 2, и нам нужна информация, которая является вторым столбцом справа от C1, который будет «B». FALSE указывает, что это должно быть точное совпадение. Копирование и вставка формул ВПР в ячейку F5 дает ранжированный список символов:
| А | Б | С | Д | Е | Ф | |
| 1 | А | 0,12% | 5 | А | 1 | Б |
| 2 | Б | 0,55% | 1 | Б | 2 | Е |
| 3 | С | 0,31% | 3 | С | 3 | С |
| 4 | Д | 0,31% | 4 | Д | 4 | Д |
| 5 | Е | 0,44% | 2 | Е | 5 | А |
Столбец F представляет собой ранжированные символы по чистому изменению в процентах.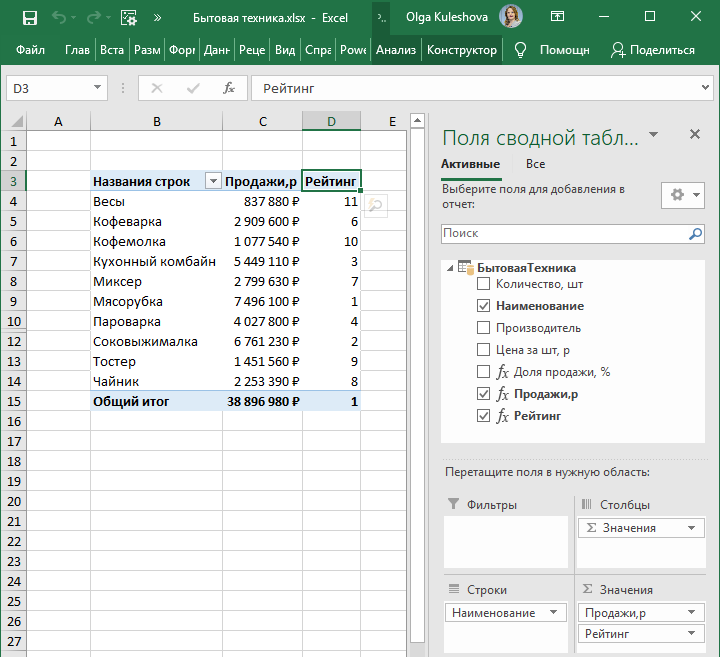
Теперь мы можем использовать ранжированные символы для получения дополнительной информации о рынке.
В загружаемом образце электронной таблицы используются вызовы RTD для пяти продуктов CME и приведенные выше формулы Excel Rank, COUNTIF и VLOOKUP. Источником этой статьи является http://www.cpearson.com/Excel/Topic.aspx.
Загрузки
Функция Excel RANK
Главная » Встроенные функции Excel » Статистические функции Excel » Функция ранжирования Excel
Статистический рейтинг
Если у вас есть статистический рейтинг чисел сообщает вам порядок значения в этом списке.
Таким образом, ранг вычисляется путем упорядочивания чисел в указанном порядке (обычно по убыванию) и последующего присвоения позиции каждому значению в списке.
.
Описание функции
Функция Excel RANK возвращает статистический ранг заданного значения в предоставленном массиве значений.
Если в списке есть повторяющиеся значения, им присваивается один и тот же ранг.
В Excel 2010 функция Rank была заменена функцией Rank.Eq. Однако функция ранжирования по-прежнему доступна в Excel 2010 (хранится в списке функций совместимости), чтобы обеспечить совместимость с более ранними версиями Excel.
Синтаксис функции Rank:
RANK( число, ссылка, [порядок] )
Где аргументы функции:
| число | — | Значение, для которого вы хотите найти ранг. | ||||||
| ref | — | Массив значений, содержащий предоставленное число. | ||||||
| [порядок] | — | Необязательный аргумент, который определяет, следует ли упорядочивать предоставленный массив ссылок в порядке возрастания или убывания. Аргумент [порядок] может иметь значение 0 или 1, что означает:
, если аргумент [порядок] опустится, он возьмет на себя обязательство по делу 0 (т. |
е. ). Любое ненулевое значение рассматривается как значение 1 (т. е. в порядке возрастания).Примеры функции ранжирования
В следующей электронной таблице показаны четыре примера функции ранжирования Excel, используемой для вычисления ранга значений в простом наборе {1, 11, 6, 9, 2, 5, 9}.
Formulas:
| Results:
|
Note that, in the above examples:
- In cells B1, B3 & B4, the [order] аргумент опущен. Таким образом, функция Rank использует нисходящий массив , 11, 9, 9, 8, 5, 2, 1 .
- В ячейке B2 аргумент [order] равен 1. Поэтому функция Rank использует возрастание 9массив 0536, 1, 2, 5, 8, 9, 9, 11 .
- Предоставленный массив содержит два значения, равные 9, которые занимают позиции 2 и 3 при ранжировании массива в порядке убывания. В этом случае функция Rank возвращает ранг 2 для значения 9 (см. пример в ячейке B3), а следующее значение, 8, имеет ранг 4 (см. ячейку B4).
Таким образом, функция Rank использует нисходящий массив , 11, 9, 9, 8, 5, 2, 1 .Дополнительную информацию и примеры функции Excel Rank см. на веб-сайте Microsoft Office.
Ошибка функции ранга
Если вы получаете сообщение об ошибке функции ранжирования Excel, это, скорее всего, ошибка #N/A:
Распространенная ошибка
| #N/A | — | поставляемый реф. (Обратите внимание, что функция Rank не распознает текстовые представления чисел как числовые значения, поэтому вы также получите ошибку #N/A, если значения в предоставленном массиве ссылок являются текстовыми значениями). |
