Априорное ранжирование факторов: Априорное ранжирование факторов методом экспертных оценок: практикум по дисциплине «Основы теории эксперимента».

Содержание

Априорное ранжирование факторов

Министерство
образование и науки

Федеральное
государственное бюджетное образовательное
учреждение

«Тихоокеанский
государственный университет»

Кафедра «Компьютерного
проектирования и сертификации машин»

Методические
указания к проведению практических
занятий и УИРС для студентов специальности
15102.65 «Металлообрабатывающие
станки и комплексы»,
200503.65
«Стандартизация и сертификация»
и 220501.65
«Управление
качеством» и 150401.65
«Проектирование
технических и технологических комплексов»

ХАБАРОВСК

2013

УДК
821.9:661.3.068

Методические
указания к проведению практических
занятий и УИРС для студентов специальностей
15102.65
«Металлообрабатывающие
станки и комплексы»,
200503.65
«Стандартизация и сертификация»,
220501. 65
«Управление
качеством» и 150401.65
«Проектирование
технических и технологических комплексов»

Методические
указания содержат краткие сведения по
методике отбора факторов и их априорного
ранжирования. Могут быть использованы
в любой области научных исследований,
где требуется провести предварительный
отбор факторов, оказывающих наибольшее
влияние на исследуемый объект. Приведено
описание программного комплекса,
предназначенного для автоматизации
ввода, обработки
и анализа
данных по результатам опроса мнений
группы специалистов-экспертов в данной
предметной области.

Методические
указания:

Разработал
к.т.н., доцент _________________________ Ю.Г.
Иванищев

Подпись

Методические
указания утверждены на заседании
кафедры

протокол
№_12_
от
«_18_»_марта_2013г.

Заведующий
кафедрой ________________
«_18_»_марта_2013г.

Подпись

ПРЕДВАРИТЕЛЬНОЕ
ОПРЕДЕЛЕНИЕ ФАКТОРНОГО ПРОСТРАНСТВА

Для
выявления факторного пространства на
первом этапе может быть использована
схема Исикава
[1,2].
Схема
представляет собой графическое
упорядочение многообразных факторов,
влияющих на объект анализа и характеризующих
конкретные результаты деятельности
или процесса. Основное достоинство
такой схемы
– наглядность
представления как о совокупности
факторов, воздействующих на объект
исследования, так и о причинно-следственных
связях этих факторов.

Построение
схемы Исикава начинается с определения
главных факторов, которые изображаются
в виде больших
(первичных)
векторов подводимых к горизонтальной
строке, направленной к объекту анализа.
Далее к каждому первичному вектору
подводят векторы второго порядка, к
которым, в свою очередь, подводят векторы
третьего порядка, и так далее. Эта
процедура повторяется до тех пор, пока
на схему не будут нанесены все факторы,
оказывающие заметное влияние на объект.

Анализ
последовательности расположения не
имеет принципиального значения.
Основным при построении схемы является
обеспечение правильности соподчиненности
и взаимозависимости факторов. А это
зависит от квалификации разработчиков
и максимальной информированности
об объекте исследования.

На
рис.1 приведен пример схемы Исикава,
иллюстрирующий общий случай воздействия
различных факторов на качество
выпускаемой предприятием продукции.

На
основе схемы Исикава могут быть выделены
основные значимые факторы для
дальнейшего их априорного ранжирования.
Процедура выделения значимых факторов
проводится в два, три этапа группой
специалистов с промежуточными
обсуждениями.

Рис.
1. Схема влияния факторов на качество
выпускаемой продукции:

1 – качество
труда; 2 – качество документации;
3 – качество средств труда;
4 – качество предметов труда: 5 –
условия труда; 6 – состояние
социально-психологического климата
в коллективе; 7 – полнота технических
требований; 8 – научно-технический
уровень; 9 – отношение к труду; 10 –
доступность изложения; 11 – правильность
оформления; 12 – профессиональная
подготовка работников; 13 – организация
труда; 14 – образование работников;
15 –
обеспеченность документацией;
16 – технологическая подготовка
производства; 17 – соответствие
современным требованиям; 18 –
метрологическое обеспечение;
19 – условия
хранения; 20 – соответствие установленным
требованиям; 21 – качество технологического
оборудования, 22 – условия транспортирования;
23 – качество инструмента; 24 – механизация
и автоматизация производства; 25 –
обеспеченность предметами труда;
26 – качество выходного контроля;
27 – обеспеченность средствами труда;
28 – качество нормировки.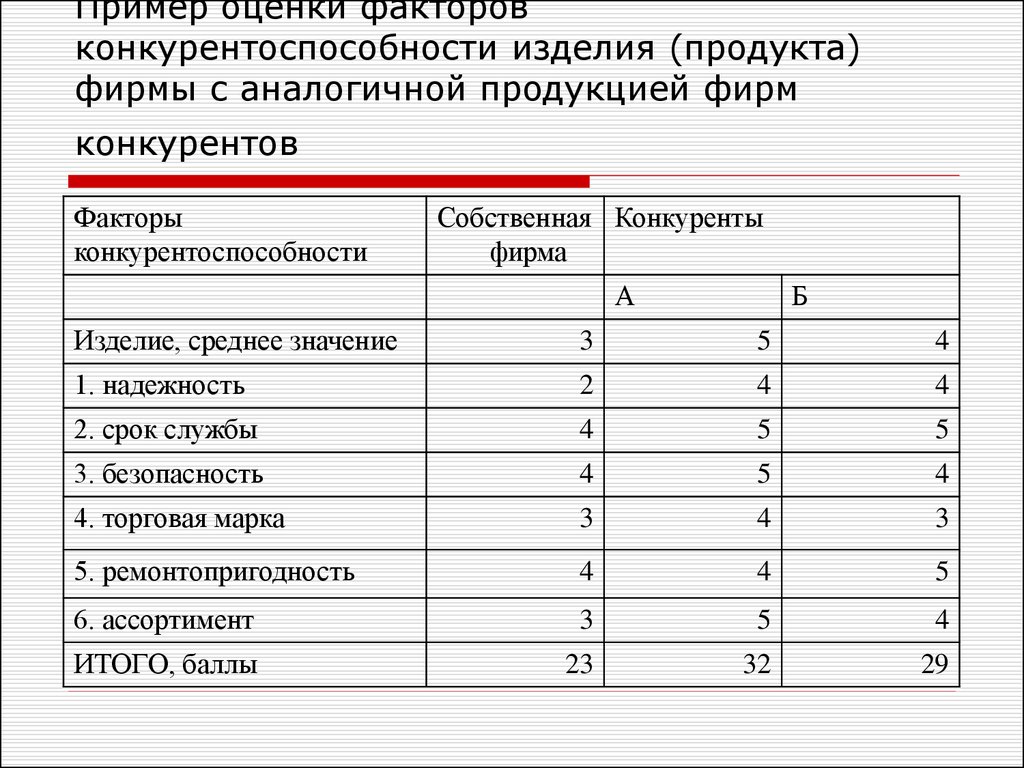

АЛГОРИТМ
РАНЖИРОВАНИЯ ФАКТОРОВ

Априорное
ранжирование факторов
– это
процедура, осуществляемая возможно
большей группой специалистов, которые
располагают предложенные заранее
факторы в порядке убывания их значимости
по степени их влияния на объект
(отклик).

Априорное
ранжирование осуществляется в несколько
этапов.

ПОСТАНОВКА
ЗАДАЧИ, ОРГАНИЗАЦИЯ И ПРОВЕДЕНИЕ
ОПРОСА

Постановка
задачи заключается в предварительном
определении факторов, значимо влияющих
на объект исследования. Эту процедуру
можно провести с помощью схемы Исикава.

Опрос
можно проводить с помощью анкетирования
или другим способом [З]. При ранжировании
каждому фактору присваивается
(по мнению
специалиста)
ранг в пределах от
1 до k
(k
– количеств
факторов).

Если два и более
факторов считаются равнозначными, им
присваиваются равные ранги.

Порядок
расположения факторов при опросе должен
быть выбран случайным. Об этом опрашиваемые
специалисты должны быть предупреждены
заранее. В противном случае, как
установлено, порядок расположения
факторов может повлиять на их ранжирование.
Для того, чтобы исключить взаимное
влияние мнений нескольких специалистов,
их опрос должен проводиться независимо
друг от друга.

Оценка значимости факторов методом априорного ранжирования

УДК 658.5.012.1

Тарасов Роман Викторович¹, Макарова Людмила Викторовна², Бахтулова Кристина Михайловна³
¹Пензенский государственный университет архитектуры и строительства, к.т.н., доцент
²Пензенский государственный университет архитектуры и строительства, к.т.н., доцент
³Пензенский государственный университет архитектуры и строительства, магистр техники и технологии

Аннотация
На начальном этапе экспериментальных исследований после выбора объекта, постановки целей и задачи эксперимента, требуется выбрать наиболее важные факторы, влияющие на параметр оптимизации.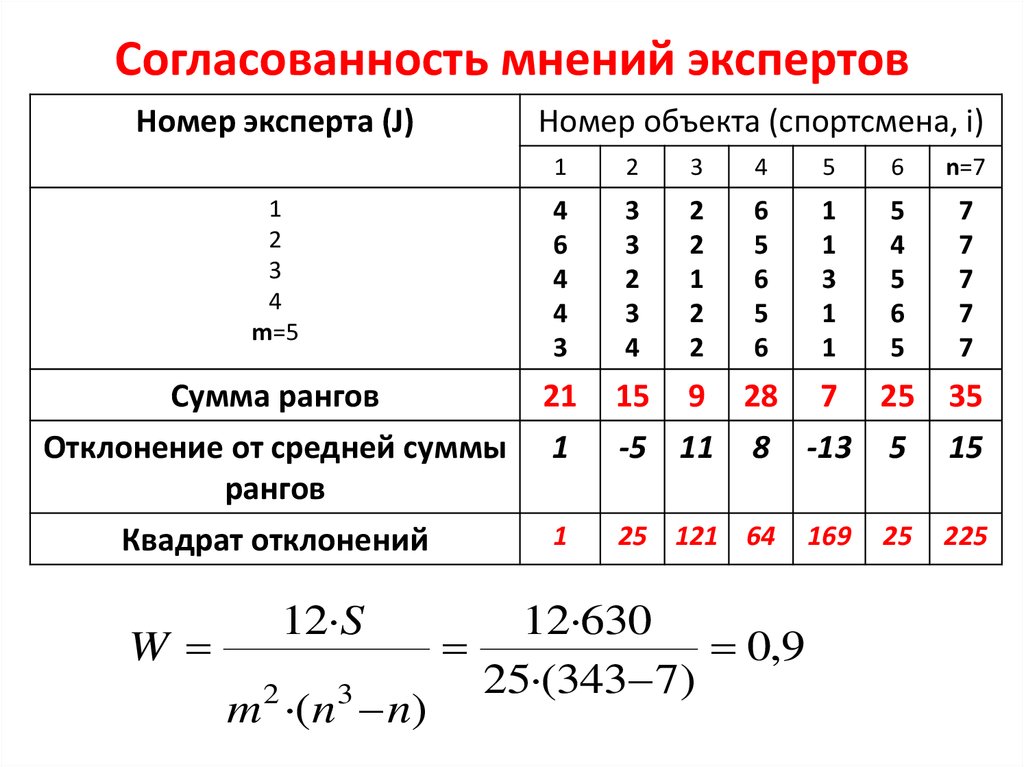 Как правило, перечень влияющих факторов достаточно широк и, учитывая тот факт, что с увеличением их количества усложняется процедура проведения эксперимента, возникает необходимость уменьшения количества факторов, включаемых в активный эксперимент. В качестве экспертного метода, позволяющего выбрать наиболее значимые факторы, можно использовать метод априорного ранжирования факторов.

Ключевые слова: априорное ранжирование факторов, планирование эксперимента, экспертные методы

Tarasov Roman Viktorovich¹, Makarova Ludmila Viktorovna², Bahtulova Christina Mikhailovna³
¹Penza State University of Architecture and Construction, Candidate of Technical Sciences, Associate Professor
²Penza State University of Architecture and Construction, Candidate of Technical Sciences, Associate Professor
³Penza State University of Architecture and Construction, master of technics and technology

Abstract
At the initial stage of experimental research after selecting the object, setting the goals and tasks of the experiment, it is required to choose the most important factors influencing on the optimization option. As a rule, the list of influencing factors is quite broad and, considering the fact that with an increase in their number the procedure of carrying out the experiment is complicated, there is the necessity of reducing the number of factors that included in the active experiment. As the expert method, allowing to choose the most significant factors, it is possible to use the method of a priori ranking factors.

Рубрика: 08.00.00 ЭКОНОМИЧЕСКИЕ НАУКИ

Библиографическая ссылка на статью:
Тарасов Р.В., Макарова Л.В., Бахтулова К.М. Оценка значимости факторов методом априорного ранжирования // Современные научные исследования и инновации. 2014. № 4. Ч. 1 [Электронный ресурс]. URL: https://web.snauka.ru/issues/2014/04/33181 (дата обращения: 16.12.2022).

Экспериментальные исследования ведутся практически во всех областях науки и техники и преследуют цель получения новых фактов об исследуемом объекте. При использовании статистического подхода к планированию эксперимента и последующей обработке экспериментальных данных необходима четкая стратегия, например, следующая последовательность действий [1]:

1. Признание факта существования задачи и ее формулировка.

2. Выбор факторов и уровней.

3. Выбор переменной отклика (параметра оптимизации).

4. Выбор плана эксперимента.

5. Проведение эксперимента.

6. Анализ данных.

7. Выводы и рекомендации.

На начальной стадии планирования эксперимента с учетом поставленных целей экспериментатор должен отобрать независимые переменные (факторы), которые в дальнейшем будут использовать в эксперименте. Как правило, факторы выбираются на основе анализа априорной информации, что требует использования различных методов систематизации полученных знаний. Для решения задач такого рода широко используются методы экспертной оценки [2]. Эти методы основаны на получении и обработке данных, полученных в результате опроса специалистов. Применительно к оценке и выбору наиболее значимых факторов широкое распространение получил метод априорного ранжирования [3].

Метод основан на ранжировании факторов в порядке убывания вносимого ими вклада. Вклад фактора оценивается по величине ранга, присвоенного конкретному фактору при ранжировании всех факторов с учетом их предполагаемого влияния на параметр оптимизации. Каждый эксперт заполняет анкету, в которой перечислены факторы, их размерность и интервалы варьирования, и определяет место фактора в ранжированном ряду.

Полученная от экспертов информация обрабатывается следующим образом:

— определяют сумму рангов по факторам

— разность (∆i) между суммой каждого фактора и средней суммой рангов

— сумму квадратов отклонений (s)

где a_ij – ранг каждого i-го фактора у j-го исследователя;

n – число исследователей;

m – число факторов;

Т – средняя сумма рангов.

Согласованность мнений экспертов оценивается с помощью коэффициента конкордации ω:

где

t_j— число одинаковых рангов в j-м ранжировании.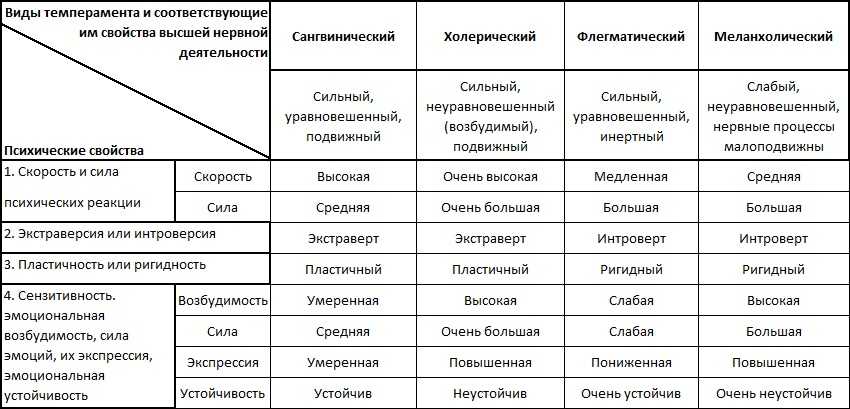

Следующим этапом является оценка значимости коэффициента конкордации оценки его значимости с помощью χ² – распределения с числом степеней свободы f = n – 1.

Значение – критерия определяют по формуле.

Гипотеза о наличии согласованности мнений исследователей может быть принята, если при заданном числе степеней свободы табличное значение χ² меньше расчетного для 5%-го уровня значимости.

Рассмотрим пример использования априорного ранжирования факторов для планирования эксперимента, предназначенного для установления зависимости влияния технологических параметров на качество плиты ДСП.

Опрос экспертов проводился с помощью анкеты, содержащей 7 факторов (k =7), которые нужно было проранжировать с учетом степени их влияния на плотность плиты ДСП. Были рассмотрены факторы, которые характеризовали условия изготовления продукции, а именно:

1. Время перемешивания стружки со смолой, отвердителем и добавками;

2. Средний размер стружки;

3. Температура прессования

4. Давление прессования;

5. Время сушки стружки

6. Время прессования

7. Температура сушки стружки;

Матрица рангов, полученная из анкет, приведена в таблице 1.

Исследователи	Факторы (n = 7)
Исследователи	X₁	X₂	X₃	X₄	X₅	X₆	X₇
1	6	7	2	5	3	4	1
2	7	6	3	5	2	4	1
3	7	6	2	5	4	3	1
4	7	6	2	5	3	4	1
5	6	7	2	4	3	5	1
	33	32	11	24	15	20	5
∆i	-13	-12	9	-4	5	0	15	S = 660
(∆i)²	169	144	81	16	25	0	225	S = 660

Несмотря на то, что полученное значение коэффициента конкордации значительно отличается от нуля, проверим его значимость по χ²-критерию:

С учетом 5%-го уровня значимости и числа степеней свободы f=6 табличное значение критерия χ² = 12,6. Следовательно, мнение экспертов согласовано. Построим среднюю диаграмму рангов для рассматриваемых факторов (рис. 1).

Рис. 1 Средняя априорная диаграмма

По результатам проведенного психологического эксперимента для дальнейшего планирования эксперимента целесообразно оставить два фактора: x₁ и x_2.

Библиографический список

Монтгомери, Д.К. Планирование эксперимента и анализ данных [Текст] / Д.К. Монтгомери – Л.: Судостроение, 1980. – 384 с.
Тарасов, Р.В. К вопросу применения экспертных методов в прогнозировании процессов, оценке уровня качества и принятии управленческих решений [Текст] / Р.В. Тарасов, Л.В. Макарова, О.Ф. Акжигитова // Современные научные исследования и инновации. – Апрель 2014. – № 4 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/04/33142.
Хамханов, К.М. Методические указания к практическим занятиям по дисциплине «Планирование эксперимента» [Текст] /К. М. Хамханов, Ю.Ж. Дондоков. – Улан-Уде: ВСГТУ, 2002.

Количество просмотров публикации: Please wait

Все статьи автора «Макарова Людмила Викторовна»

Определение априорной вероятности, формула, пример

От

Уилл Кентон

Полная биография

Уилл Кентон — эксперт в области экономики и инвестиционного законодательства. Ранее он занимал руководящие должности редактора в Investopedia и Kapitall Wire, имеет степень магистра экономики Новой школы социальных исследований и степень доктора философии по английской литературе Нью-Йоркского университета.

Узнайте о нашем
редакционная политика

Обновлено 17 ноября 2021 г.

Рассмотрено

Сомер Андерсон

Рассмотрено
Сомер Андерсон

Полная биография

Сомер Дж. Андерсон является дипломированным бухгалтером, доктором бухгалтерского учета и профессором бухгалтерского учета и финансов, который работает в сфере бухгалтерского учета и финансов более 20 лет. Ее опыт охватывает широкий спектр областей бухгалтерского учета, корпоративных финансов, налогов, кредитования и личных финансов.

Узнайте о нашем
Совет финансового контроля

Факт проверен

Кэтрин Бир

Факт проверен
Кэтрин Бир

Полная биография

Кэтрин Бир — писатель, редактор и архивариус из Нью-Йорка. У нее большой опыт исследовательской и писательской деятельности, она освещала такие разнообразные темы, как история общественных садов Нью-Йорка и выступление Бейонсе на фестивале Coachella в 2018 году.

Узнайте о нашем
редакционная политика

Что такое априорная вероятность?

Априорная вероятность относится к вероятности возникновения события, когда существует конечное количество исходов, и каждый из них имеет одинаковую вероятность. Исходы с априорной вероятностью не зависят от предыдущего исхода. Или, другими словами, любые результаты на сегодняшний день не дадут вам преимущества в прогнозировании будущих результатов. Подбрасывание монеты обычно используется для объяснения априорной вероятности. Вероятность выпадения орла или решки составляет 50% при каждом подбрасывании монеты, независимо от того, выпадет ли у вас серия орлов или решек. Самым большим недостатком этого метода определения вероятностей является то, что его можно применять только к конечному набору событий, поскольку большинство реальных событий, которые нас интересуют, в той или иной степени подвержены условной вероятности. Априорная вероятность также называется классической вероятностью.

Ключевые выводы

Априорная вероятность предполагает, что исход следующего события не зависит от исхода предыдущего события.
Априори также удаляет опыт независимых пользователей. Поскольку результаты случайны и не зависят от обстоятельств, вы не можете вывести следующий результат.
Хорошим примером этого является подбрасывание монеты. Независимо от того, что было перевернуто раньше или сколько раз произошло, шансы всегда равны 50%, поскольку есть две стороны.

Понимание априорной вероятности

Априорная вероятность в значительной степени является теоретической основой для вероятностей, которые могут быть ограничены небольшим числом результатов. Формула для расчета априорной вероятности очень проста:

Априорная вероятность = желаемый результат(ы)/общее количество результатов

Таким образом, априорная вероятность того, что на шестигранном кубике выпадет шестерка, равна единице (желаемый результат — шесть), деленной на шесть. Таким образом, у вас есть 16% шанс выбросить шестерку и точно такой же шанс с любым другим числом, которое вы выберете на кубиках. Конечно, априорные вероятности могут быть объединены в набор результатов, поэтому ваши шансы выбросить четное число на одном и том же кубике увеличиваются до 50% просто потому, что желаемых результатов больше.

Реальный пример априорной вероятности

Повседневный пример априорной вероятности — ваши шансы выиграть в лотерею, основанную на числах. Формула для расчета вероятности становится намного сложнее, поскольку ваши шансы основаны на комбинации чисел в билете, выбранной случайным образом в правильном порядке, и вы можете купить несколько билетов с несколькими комбинациями чисел. Тем не менее, существует ограниченный набор комбинаций, которые приведут к выигрышу. К сожалению, количество возможных результатов затмевает количество желаемых результатов — вашего конкретного набора билетов. Вероятность выиграть главный приз в такой лотерее, как лотерея Powerball в США, составляет один к сотням миллионов. Более того, шансы выиграть главный приз исключительно (без разделения) снижаются по мере увеличения банка и увеличения количества игроков.

Априорная вероятность и финансы

Применение априорной вероятности к финансам ограничено. Помимо отговорки людей от того, чтобы доверить свою финансовую судьбу лотерее, большинство результатов, о которых заботятся финансисты, не имеют конечного числа результатов. Вы не можете сказать, что у цены акции есть три возможных исхода: рост, падение или неизменность, когда на эти исходы влияет ряд внешних факторов, которые изменяют вероятность каждого исхода.

В финансах люди чаще используют эмпирическую или субъективную вероятность, а не классическую вероятность. В эмпирической вероятности вы смотрите на прошлые данные, чтобы получить представление о том, какими будут результаты в будущем. С субъективной вероятностью вы накладываете свой личный опыт и точки зрения на данные, чтобы сделать уникальный для вас звонок. Если акции были на разрыве в течение трех дней после того, как превзошли рекомендации аналитиков, инвестор может обоснованно ожидать, что они продолжатся, основываясь на недавнем ценовом действии. Однако другой инвестор может увидеть такое же движение цены и вспомнить, что консолидация последовала за резким ростом этих акций два года назад, принимая противоположное сообщение из тех же ценовых данных. В зависимости от рынка, оба инвестора могут быть не более точными, чем предсказание с помощью априорной вероятности, но мы чувствуем себя лучше, когда принимаем решения, которые можем обосновать хотя бы некоторой логикой, помимо случайности.

11.5 Априорный выбор | САМАЯ ХУДШАЯ СТАТИСТИКА

Самый распространенный подход к выбору модели — это, вероятно, , предшествующий выбору модели . Это означает рассмотрение только тех моделей, для которых у нас есть априорных причин для включения. Обычно это модели, предназначенные для представления конкурирующих [биологических] гипотез или для уравновешивания этих гипотез в рамках проверки. В простых ситуациях мы сравниваем все интересующие нас модели посредством одного этапа выбора модели. Будет придерживаться этого подхода для класса. Но в более сложных ситуациях мы могли бы применить иерархический (многоэтапный) подход, чтобы уменьшить сложность и проверять гипотезы о конкретных группах параметров по одной, чтобы избежать завышенной частоты ошибок типа I (да, это все еще актуально!), когда у нас есть много-много моделей.

11.5.1 Многоэтапный (иерархический) отбор

Иерархический выбор модели широко используется для сложных моделей, которые имеют различные лежащие в основе процессы (и часто «вероятности»). Отличным примером таких моделей являются модели занятости и метки-повторного захвата, которые включают «подмодели» для оценки вероятности обнаружения и другие «подмодели» для оценки таких вещей, как присутствие-отсутствие, выживание или изобилие. Эти методы широко используются в исследованиях популяций рыб и диких животных, а также являются краеугольным камнем современной эпидемиологии, когда мы хотим объяснить ложноположительные или ложноотрицательные результаты.

По сути, многоэтапный выбор модели означает, что мы налагаем некоторую иерархию на шаги, предпринимаемые для проверки конкурирующих гипотез. Например, мы могли бы сначала сравнить гипотезы о факторах, влияющих на вероятность обнаружения в наших примерах выше. Затем мы могли бы использовать лучшие модели из этого набора гипотез в качестве основы для проверки гипотез о факторах, влияющих на такие процессы, как выживание или вероятность размножения.

11.5.3 Инструменты для

априори выбор модели

Здесь мы сосредоточимся на нескольких общих подходах к выбору модели, которые могут быть полезны в различных ситуациях. Мы также обсудим важность размышлений о гипотезах, представленных нашими моделями, и о том, как результаты выбора модели интерпретируются по ходу дела. В этой области выбора модели важно, чтобы мы ограничивали количество рассматриваемых моделей, чтобы избежать введения ложных гипотез и ненужных выводов. Помните, теперь независимо от того, какую модель мы выберем как лучшую, она не может представлять хорошую гипотезу, если мы не знаем, что она означает. И, несмотря ни на что, у нас всегда будет лучшая модель, даже если самая лучшая модель — дерьмовая.

По словам великого Скробиуса Пипа в его Смерти журналиста :
> Бросай в стену достаточно дерьма, и часть его прилипнет
Но не заблуждайтесь, ваша стена все еще покрыта дерьмом

Чтобы убедиться, что наши стены вообще не покрыты экскрементами, мы рассмотрим историческое применение и трудности статистики Скорректированного R ², а затем мы углубимся в теоретико-информационные подходы с использованием информационного критерия Акаике (AIC), поскольку он, наряду с другими информационными критериями, в настоящее время является основным методом, используемым для выбора модели.

Давайте проверим некоторые из этих инструментов!

Начните с подгонки некоторых моделей. На этой неделе мы снова будем использовать данные swiss для демонстрации инструментов выбора, потому что это зашумленный набор данных с большой сложностью и коллинеарностью между переменными.

 данные ("швейцарские")
# Соответствуйте модели, которая тестирует
# влияние образования на индекс рождаемости
mod_Ed <- lm(Рождаемость ~ Образование, данные = швейцарские)
# Установите другую модель, которая тестирует
# эффекты % католика на фертильность
mod_Cath <- lm (фертилити ~ католик, данные = швейцарский)
# Подобрать модель с аддитивными эффектами
# обеих независимых переменных
mod_EdCath <- lm (рождаемость ~ образование + католицизм, данные = швейцарцы)
# Соответствуйте модели с мультипликативным
# влияние обеих независимых переменных
mod_EdxCath <- lm(Рождаемость ~ Образование * Католик, данные = швейцарский)

У нас есть четыре модели, представляющие конкурирующие гипотезы:

1. Образование Одно лишь лучшее объяснение среди рассмотренных для изменчивости рождаемости .

2.Процент Католик Одно только является лучшим объяснением среди рассмотренных для изменчивости рождаемости .

3. Аддитивные эффекты Образование и процент Католик являются лучшим объяснением среди рассмотренных для изменчивости в плодородие .

4. Интерактивные эффекты Образование и процент католиков являются лучшим объяснением среди рассмотренных для изменчивости рождаемости .

Отлично, но как мы можем оценить, какая из этих гипотез лучше всего подтверждается нашими данными?

Взгляните на остатки самой сложной из этих моделей, чтобы убедиться, что мы не нарушили предположения линейных моделей. В данном случае «наиболее сложная» означает модель с наибольшим количеством параметров, или мод.EdxCath . Если вы все еще не уверены, почему эта модель имеет больше параметров, чем mod.EdCath , посмотрите на вывод model.matrix() для каждого из них.

 # Извлечь остатки из
# подогнанный объект модели
остатки <- mod_EdxCath$остатки
# Добавляем остатки к швейцарским данным
swiss_resids <- data.frame(swiss, resids)

Они определенно выглядят нормально со средним значением, равным нулю:

 ggplot(swiss_resids, aes(x = resids)) +
  geom_histogram (ячейки = 5)

Взгляд на остатки по сравнению с подобранными, по-видимому, указывает на то, что у нас нет каких-либо значимых закономерностей в остатках по отношению к наблюдаемому значению рождаемости, хотя мы видим, что одна точка сама по себе слева, что может заставить нас хотеть блевать немного.

 # Сделайте красивый сюжет, чтобы убедиться, что мы не
# совсем забыл про этих надоедливых
# предположения из главы 9
ggplot (mod_EdxCath, aes (x = .fitted, y = .resid)) +
  геом_джиттер() +
  geom_abline (перехват = 0, наклон = 0) +
  xlab("Рождаемость") +
  ylab(выражение(вставить(эпсилон))) +
  тема_bw()

Теперь, когда мы убедились, что не нарушаем допущения, мы можем применить выбор модели, чтобы выяснить, явно ли одна лучше других, и если да, то какая. Затем мы будем использовать нашу лучшую модель, чтобы делать прогнозы, как на прошлой неделе, и на следующей неделе, и на следующей неделе… и так далее.

Давайте начнем с создания списка наших моделей и присвоения каждому элементу (модели) в списке имени:

 # Создание списка, содержащего модели внутри него
моды <- список (mod_Ed, mod_Cath, mod_EdCath, mod_EdxCath)
# Дайте имена каждому элементу списка (каждой модели)
имена(моды) <- c("Ed", "Cath", "EdCath", "EdxCath")

11.5.3.1 Скорректированный R

Скорректированный R ² предлагает относительно простой инструмент для выбора модели. Он превосходит множитель R ², с которым мы работали, только потому, что уравновешивает количество параметров в модели с количеством наблюдений в наших данных.

Как и раньше, мы можем просмотреть сводку объектов нашей модели, которые мы сохранили в этом списке.

 # Образовательная модель, можно посмотреть, вот так
резюме (моды $ Эд)

 ##
## Вызов:
## lm(formula = Fertility ~ Education, data = swiss)
##
## Остатки:
## Мин.  1 кв. Медиана 3 кв. Макс.
## -17,036 -6,711 -1,011 9,526 19,689
##
## Коэффициенты:
## Оценить стандарт. Значение ошибки t Pr(>|t|)
## (Перехват) 79,6101 2,1041 37,836 < 2e-16 ***
## Образование -0,8624 0,1448 -5,954 3,66e-07 ***
## ---
## Значение. коды: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 '' 1
##
## Остаточная стандартная ошибка: 9,446 при 45 степенях свободы
## Множественный R-квадрат: 0,4406, скорректированный R-квадрат: 0,4282
## F-статистика: 35,45 на 1 и 45 DF, p-значение: 3,659e-07

 # ПОМНИТЕ: эта модель представляет собой объект, хранящийся в R,
# так что мы также можем посмотреть на имена этого резюме,
# как это
name(summary(mods$Ed))

 ## [1] "вызов" "термы" "остатки" "коэффициенты"
## [5] "aliased" "sigma" "df" "r.squared"
## [9] "adj.r.squared" "fstatistic" "cov.unscaled"

Ого, , это тяжелая штука. Напомним, что мы составили список моделей, каждая из которых на самом деле является списком. Каждая модель имеет множество элементов. Выход summary() для каждой модели также является списком, и элементы имеют собственные имена. В этом окончательном списке мы можем найти Adusted R-squared или то, что summary() называет adj.r.squared . Это черепахи снова и снова.

Конечно, мы можем извлечь скорректированное значение R ² из вывода summary() по имени:

 ed_r <- summary(mods$Ed)$adj.r.squared
cath_r <- summary(mods$Cath)$adj.r.squared
EdCath_r <- summary(mods$EdCath)$adj.r.squared
EdxCath_r <- summary(mods$EdxCath)$adj.r.squared

И мы могли бы даже поместить их во фрейм данных с оригинальными названиями моделей, чтобы сравнить значения R ².

 данных.кадр(
  модель = имена (моды),
  adj_r_squared = c(ed_r, кат_r, EdCath_r, EdxCath_r)
)

 ## модель adj_r_squared
## 1 Эд 0.4281849
## 2 Кат 0.1975591
## 3 EdCath 0.5551665
## 4 EdxCath 0.5700628

При сравнении скорректированных R ² , модель с наибольшим R ² является «лучшей моделью» . Итак, в данном случае мы бы сделали вывод, что EdxCath — лучшая модель. Но у нас есть две проблемы. Во-первых, как определить, статистически значимо ли значение R ², равное 0,57, чем значение R ², равное 0,57? Во-вторых, мы знаем, что в EdxCath больше параметров, чем в EdxCath . Стоят ли эти дополнительные параметры небольшой прибавки в ² руб?. Хотя мы не будем углубляться в статистику, подобную статистике PRESS, эта и другие традиционные статистические данные о выборе модели страдают теми же двумя недостатками. Наконец, Р ² — это статистика, полученная из суммы квадратов ошибок в оценке методом наименьших квадратов, поэтому мы не сможем использовать ее, начиная с главы 12, когда мы начнем оценивать коэффициенты регрессии с использованием оценки максимального правдоподобия.

Итак, как жить?

11.5.3.2 Подходы теории информации

Информационный критерий Акаике (AIC)

Этот инструмент (или популярные альтернативы BIC, DIC и WAIC) будет более полезен для нас в течение следующих нескольких недель, чем любой из методов, которые мы обсуждали до сих пор, потому что он позволяет нам делать выводы на основе вероятности модель, а не сумма квадратов ошибок, которых, как мы узнаем, нет в GLM и других обобщениях!

Информационно-теоретические подходы к выбору модели основаны на компромиссе между информацией, полученной за счет добавления параметров (независимых переменных и способов их сочетания) и дополнительной сложностью моделей по отношению к размеру выборки. Я воздержусь от подробного объяснения, потому что вы узнаете больше об этом инструменте в своих чтениях. Итак, давайте сразу к делу.

Помните, что мы составили список априорных моделей выше, которые мы хотели бы рассмотреть.

Взгляните на названия этих моделей на случай, если вы их забыли.

 name(mods)

 ## [1] "Ed" "Cath" "EdCath" "EdxCath"

Мы можем извлечь значение AIC для каждой модели в нашем списке, используя lapply() или mapply функции. Эти функции будут разделять список и «применять» функцию к каждому из элементов этого списка. Основное отличие состоит в том, что lapply() возвращает именованный список, а mapply() возвращает атомарный вектор с именованными элементами (с ним проще работать, если мы хотим объединить результаты с именами моделей).

 mods_AIC <- mapply (FUN = "AIC", моды)
данные.кадр(
  Модель = имена (моды),
  AIC = моды_AIC
)

 ## Модель AIC
## Эд Эд 348. 4223
## Кэт Кэт 364.3479
## EdCath EdCath 337.5636
## EdxCath EdxCath 336.8823

Теперь мы напечатали фрейм данных с именами наших моделей в одном столбце и их значениями AIC в другом. В отличие от Р² статистика, чем меньше, тем лучше, когда речь идет об AIC (и других подходах к ИТ), даже если значения отрицательные. Фактическое значение AIC для любой данной модели не имеет никакой интерпретации, кроме как относительно оставшихся трех . Уточняю: если у меня одно значение AIC для одной модели, то это бессмысленно. У меня должна быть другая модель с таким же откликом (и данными!!) для сравнения. Не существует такого понятия, как «хороший» или «плохой» AIC по своей сути. Они интерпретируются только относительно других моделей в том же наборе кандидатов. Это принципиально отличается от R ² статистика.

С первого взгляда видно, что наша модель с взаимодействием является «лучшей» моделью в наборе, как показывают другие наши статистические данные, но на этот раз она лучше только менее чем на 1 AIC ( чем ниже AIC, тем лучше ). Можем ли мы что-нибудь сказать об этом?

Забавно, что вы должны спросить. Да мы можем. У нас есть несколько общих эмпирических правил для интерпретации статистики AIC, и мы можем получить целый набор статистических данных на основе этих рейтингов.

Открытая банка червей…

 # Во-первых, нам нужна еще одна библиотека
библиотека (AICcmodavg)
# Давайте начнем копаться в этом материале
# создав таблицу, которая может нам помочь.
aictab(cand.set = моды, имена модов = имена (моды))

 ##
## Выбор модели на основе AICc:
##
## K AICc Delta_AICc AICcWt Суммарная масса LL
## EdxCath 5 338,35 0,00 0,52 0,52 -163,44
## EdCath 4 338,52 0,17 0,48 1,00 -164,78
## Изд 3 348,98 10,63 0,00 1,00 -171,21
## Кат 3 364,91 26.56 0.00 1.00 -179.17

Здесь много чего происходит… Что все это значит ?

Пройдемся по столу Слева направо. Во-первых, обратите внимание, что row.names() на самом деле являются именами наших моделей, что приятно. Далее следует принять к сведению, что модели ранжированы в порядке возрастания AIC. Имея некоторый контекст, мы можем посмотреть на каждый столбец следующим образом:

K — количество параметров в каждой из моделей

AICc — это оценка AIC, но она скорректирована с учетом размера выборки. Вообще говоря, это означает, что модели с большим количеством параметров и небольшим количеством наблюдений наказываются потенциальной нестабильностью вероятности. В общем, использование AIC _c почти всегда является практичным подходом, потому что он консервативен, когда у нас мало данных, а эффект штрафа исчезает при достаточно больших размерах выборки (поэтому он становится эквивалентным AIC).

Delta_AICc — разница в AIC _c между лучшей моделью и каждой из других моделей.

AICcWt — вероятность того, что данная модель является лучшей моделью в наборе кандидатов.

Cum.Wt — совокупный вес, представленный каждой из моделей от лучшей до последней. Это можно использовать для создания набора моделей с доверительной вероятностью 95%.

LL - это логарифмическая вероятность каждой модели, то же самое, что обсуждалось в начале наших обсуждений вероятностных распределений!

11.5.3.4 Усреднение модели

Используя усреднение модели для учета неопределенности модели, мы можем видеть, что безусловный доверительный интервал для Образование отрицателен и не перекрывает ноль, а в тренде для очевидна обратная тенденция Католик . Мы также обнаруживаем, что взаимодействие между Образование и Католик на самом деле незначительно, что, вероятно, является причиной того, что модель главных эффектов имела эквивалентную поддержку в наборе кандидатов.

 modavg(моды,
  parm = "Образование", modnames = имена (моды),
  conf. level = .95, исключить = TRUE
)

 ##
## Мультимодельный вывод по «Образованию» на основе AICc
##
## Таблица AICc, используемая для получения усредненной по модели оценки:
##
## K AICc Delta_AICc AICcWt Оценка SE
## Эд 3 348,98 10,63 0,00 -0,86 0,14
## EdCath 4 338,52 0,17 0,48 -0,79 0,13
## EdxCath 5 338,35 0,00 0,52 -0,43 0,26
##
## Усредненная по модели оценка: -0,6
## Безусловный SE: 0,28
## 95% Безусловный доверительный интервал: -1,14, -0,06

 modavg(mods,
  parm = "Католик", modnames = имена (моды),
  conf.level = .95, исключить = TRUE
)

 ##
## Мультимодельный вывод о "католике" на основе AICc
##
## Таблица AICc, используемая для получения усредненной по модели оценки:
##
## K AICc Delta_AICc AICcWt Оценка SE
## Кат 3 364,91 26,56 0,00 0,14 0,04
## EdCath 4 338,52 0,17 0,48 0,11 0,03
## EdxCath 5 338,35 0,00 0,52 0,18 0,05
##
## Усредненная по модели оценка: 0,15
## Безусловный SE: 0,06
## 95% Безусловный доверительный интервал: 0,04, 0,26

 modavg(mods,
 parm = "Образование: католическое", modnames = имена (моды),
 conf.