Задачи оптимизации: Постановка задачи оптимизации и численные методы ее решения

Задача оптимизации | это… Что такое Задача оптимизации?

ТолкованиеПеревод

Задача оптимизации

Задачей оптимизации в математике называется задача о нахождении экстремума (минимума или максимума) вещественной функции в некоторой области. Как правило, рассматриваются области, принадлежащие и заданные набором равенств и неравенств.

Содержание 1 Постановка задачи оптимизации 2 Классификация методов оптимизации 3 Литература 4 Ссылки

Постановка задачи оптимизации

Для того, чтобы корректно поставить задачу оптимизации необходимо задать:

1. Допустимое множество — множество ;
2. Целевую функцию — отображение ;
3. Критерий поиска (max или min).

Тогда решить задачу означает одно из:

1. Показать, что .
2. Показать, что целевая функция не ограничена.
3. Найти .
4. Если , то найти .

Если минимизируемая функция не является выпуклой, то часто ограничиваются поиском локальных минимумов и максимумов: точек x₀ таких, что всюду в некоторой их окрестности для минимума и для максимума.

Если допустимое множество , то такая задача называется задачей безусловной оптимизации, в противном случае — задачей условной оптимизации.

Классификация методов оптимизации

Методы, по средством которых решают задачи оптимизации, подразделяются на виды, соответствующие задачам, к которым они применяются:

• Локальные методы (задача оптимизации унимодальной целевой функции).
• Глобальные методы (имеют дело с многоэкстремальными целевыми функциями. При глобальном поиске основной задачей является выявление тенденций глобального поведения целевой функции.).

Существующие в настоящее время методы поиска можно разбить на три большие группы:

1. детерминированные;
2. случайные;
3. комбинированные.

Некоторые детерминированные методы:

• Задачи оптимизации, в которых целевая функция и ограничения являются линейными функциями, разрешаются так называемыми методами линейного программирования.
• В противном случае имеют дело с задачей нелинейного программирования и применяют соответствующие методы. В свою очередь из них выделяют две частные задачи:
  • если и  — выпуклые функции, то такую задачу называют задачей выпуклого программирования;
  • если , то имеют дело с задачей целочисленного (дискретного) программирования.

Помимо того, оптимизационные методы делятся на следующие группы:

• аналитические методы;
• численные методы;
• графические методы.

Также они разделяются по критерию размерности допустимого множества на методы одномерной оптимизации и методы многомерной оптимизации.

Литература

1. Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. пец. вузов. — М.: Высшая школа, 1986.
2. Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М.: Мир, 1985.
3. Коршунов Ю.М., Коршунов Ю.М. Математические основы кибернетики. — М.: Энергоатомиздат, 1972.
4. Максимов Ю.А.,Филлиповская Е.А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
5. Максимов Ю.А. Алгоритмы линейного и дискретного программирования. — М.: МИФИ, 1980.
6. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.
7. Жиглявский А.А., Жилинкас А.Г. Методы поиска глобального экстремума. — М.: Наука, Физматлит, 1991.
8. Растригин Л.А. Статистические методы поиска. — М.: 1968.
9. Абакаров А.Ш., Сушков Ю.А. Статистическое исследование одного алгоритма глобальной оптимизации. — Труды ФОРА, 2004.

Ссылки

• MDOP — Поиск глобального оптимума для задач оптимального проектирования систем или определения оптимальных законов управления.
• Глобальная оптимизация, принятие решений — Программные системы поддержки принятия оптимальных решений. Глобальные алгоримы.

Wikimedia Foundation.
2010.

Игры ⚽ Поможем решить контрольную работу

• Задача о четырёх красках
• Задача трех тел

Полезное

Оптимизационные задачи, их классификация

Оптимизационная
задача задаётся тройкой
,
гдеF
– функция, определённая на множестве
,
аD
– некоторое подмножество множества
.

Функция
F
называется целевой
функцией;

D
– множеством
допустимых
решений (допустимой
областью)

оптимизационной
задачи;

_{U—
пространством оптимизации.}

Оптимизационная
задача максимизации

(минимизации)
состоит в отыскании наибольшего
(наименьшего) значения целевой функции
F
на допустимом
множестве
D.

Любая задача
максимизации
сводится к задаче минимизации.

Решить оптимизационную
задачу – значит найти её оптимальное
решение, либо установить неразрешимость
этой задачи. Например, задача максимизации
(минимизации)
будет неразрешимой, если щелевая функцияF
неограниченна сверху (снизу) на множестве
D.

_{Методы решения
оптимизационных задач зависят как от
вида целевой функции} F,
так и от вида множества допустимых
решения D.
_{— оптимизируемая целевая функция, или
целевой функционал , критерий качества
— численно выражает степень достижения
целей функционирования оптимизируемого
объекта. Целевая функция
представляет собой набор критериев
качества, которые должны быть оптимизированы
одновременно. Соответственно, приk=1
имеем задачу однокритериальной
или скалярной
оптимизации, а при k>1
– задачу многокритериальной
или векторной
оптимизации.}

_{Вектор неизвестных
может
содержать одну компоненту (n=1)
и тогда мы имеем задачу одномерной
оптимизации, а может иметь и много
составляющих (n>1)
и тогда это задача многомерной
оптимизации
или задача
оптимизации со многими
переменными.}

_{Допустимая
область
Dможет
совпадать с пространством оптимизации
(D
=U), что
означает отсутствие каких-либо ограничений
на неизвестные. В этом случае имеем
задачу безусловной
оптимизации
или задачу
оптимизации без
ограничений.
Если же
,
то в задаче не все значения переменных
допустимы, т. е. имеются некоторые
ограничения на них. Соответствующая
задача оптимизации называетсяусловной
или задачей
с ограничениями.}

_{Пространство
оптимизации
Uможет
совпадать с евклидовым пространством
и мы получаем задачу
оптимизации с
непрерывными переменными.}

_{Если переменные
являются целочисленными, то соответствующая
задача носит название целочисленной
оптимизации.
Частным
случаем целочисленной оптимизации
является булевая
оптимизация,
при которой переменные могут принимать
только два значения – ноль и единица.
Если при этом целевая функция принимает
значения из множества вещественных
чисел, то такая задача называется задачей
псевдобулевой
оптимизации,
чтобы
подчеркнуть ее отличие от случая, когда
и значения функции тоже являются нулем
или единицей.}

_{Если же значение
целевой функции зависит от некоторых
комбинаций объектов из конечного набора,
их размещения или способа упорядочения,
то такие задачи называются задачами
комбинаторной
оптимизации.}

_{Задачи
целочисленной и комбинаторной оптимизации
объединяются понятием задач дискретной
оптимизации.
Наконец,
существуют задачи смешанной
оптимизации,
в которых могут одновременно присутствовать
переменные всех типов. Наиболее известным
случаем таких задач являются дачи
смешанного
целочисленного
программирования с целочисленными и
непрерывными переменными.}

_{Приведем
классификацию задач оптимизации с
учетом конкретной формы задачи и свойств
функции, входящих в ее постановку, как
это сделано в работе [15]}

_{Прежде всего
целевая функция и функции, описывающие
ограничения, могут быть заданы не
аналитически, а в виде компьютерных
программ, имитационных моделей,
человеко-машинных процедур или даже
как выход реальной системы.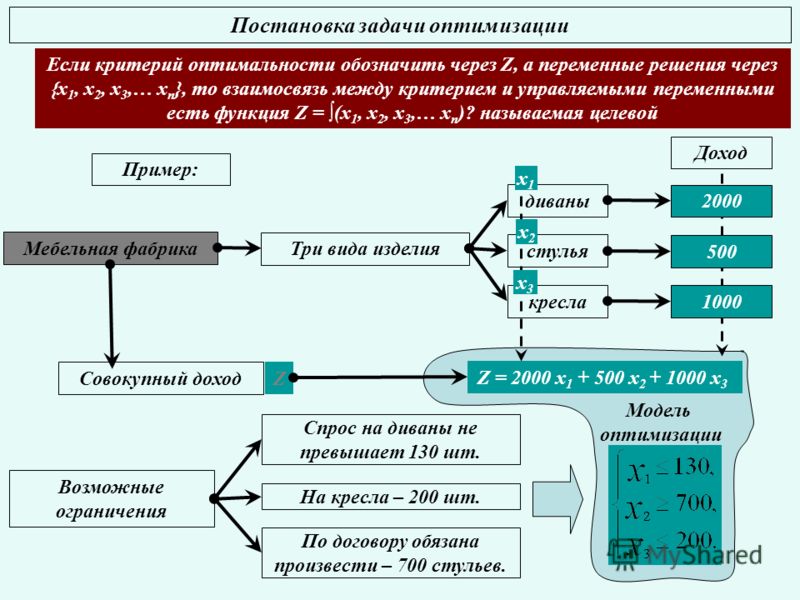 Такие задачи
оптимизации называют задачами оптимизации
с неявными функциями или поисковыми
задачами оптимизации.
Процесс оптимизации в таком случае
больше похож на экспериментирование,
чем на вычисление.}

_{Если же все
функции, входящие в постановку задачи,
записываются в явном аналитическом
виде ,
то соответствующая задача оптимизации
называется задачей математического
программирования.
Чаще всего математическим
программированием называют задачи
оптимизации с ограничениями, подчеркивая
их отличие от задач безусловной
оптимизации.}

В математическом
программировании основными разделами
являются: линейное программирование,
целочисленное, выпуклое программирование.

Оптимизационная
задача
,
в которой целевая функцияF является
линейной функцией на
,
аD
является
множеством решений некоторой системы
линейных уравнений и линейных неравенств
от
неизвестных, называетсязадачей
линейного программирования.
Систему линейных уравнений и неравенств,
определяющую множество D
, называют
системой
ограничений
задачи линейного программирования.

_{Существуют
более узкие постановки задачи линейного
программирования – транспортная задача,
задача о назначениях, задача целочисленного
линейного программирования и другие.}

_{Если целевая
функция сепарабельна, т.е. изменяется
независимо по каждой переменной в
отдельности, а ограничения – линейны,
то задача называется задачей сепарабельного
программирования.}

_{Если целевая
функция квадратична, а ограничения –
линейны, то задача называется задачей
квадратичного
программирования.}

_{Если целевая
функция выпукла, а функции-ограничения
образуют выпуклую допустимую область,
то соответствующая задача носит название
задачи выпуклой
оптимизации.}

_{В случае функций
общего вида говорят об общей задаче
нелинейного
программирования.}

_{Предполагалось
также,
что
все функции и коэффициенты, входящие в
постановку задачи являются постоянными
величинами, а они могут на самом деле
зависеть от некоторого параметра или
параметров. В таком случае нужно изучать
поведение оптимального решения при
изменении исходных данных задачи,
разрабатывать методы, позволяющие
находить оптимальный план сразу для
совокупности значений параметров.
Соответствующие задачи получили название
параметрических
задач оптимизации,
а этот раздел методов оптимизации
называется параметрическим
программированием.}

_{Наконец, до сих
пор, опять таки неявно, предполагалось,
что вся исходная информация определена
однозначно. Такие задачи называются
детерминированными.
Такие модели могут оказаться неадекватными
реальным процессам, которые могут
характеризоваться неполнотой, неточностью
данных, на основе которых формируется
модель.}

_{В ситуациях,
когда все или некоторые параметры модели
носят вероятностный характер, говорят
опринятии
решения в условиях риска
и соответствующие оптимизационные
задачи называют стохастическими,
а соответствующий раздел теории –
стохастическим
программированием
или стохастической аппроксимацией.}

_{Однако
неопределенность данных задачи может
иметь и не вероятностный характер. В
таких ситуациях говорят об
оптимизации в условиях неопределенности.
Методы решения в таких случаях основываются
на теории нечетких
множеств
и так называемой нечеткой
логике
и объединяются под названием нечеткого
математического программирования
или нечеткой
оптимизации.}

Как решить задачи оптимизации в исчислении — Matheno.com

Нужно решить задачи оптимизации в исчислении? Давайте разберем их и разработаем стратегию, которую вы сможете использовать, чтобы решать их самостоятельно.

Обзор

Задачи оптимизации всегда будут просить вас максимизировать или минимизировать какое-то количество, описав ситуацию словами (вместо того, чтобы сразу дать вам функцию максимизировать/минимизировать). Типичные фразы, указывающие на проблему с оптимизацией, включают:

• Найдите самый большой ….
• Найдите минимум….
• Какие размеры дадут наибольшее…?

Каждая из этих фраз должна наводить вас на мысль: «Я ищу максимальное (или минимальное) значение».

Большинство студентов не понимают, что вам нужно пройти два разных этапа.

Прежде чем вы сможете искать это максимальное/минимальное значение, вам сначала нужно разработать функцию, которую вы собираетесь оптимизировать. Таким образом, для полного решения этих проблем существует два отдельных этапа — то, что большинство студентов изначально не осознают [Ссылка].

Первый этап вообще не связан с исчислением, в то время как второй этап представляет собой просто задачу на макс/мин, которую вы недавно научились решать:

Этап I. Разработайте функцию. Сначала вы должны преобразовать описание ситуации в функцию — и, что особенно важно, в функцию, которая зависит только от одной единственной переменной .

Этап II. Максимизируйте или минимизируйте эту функцию. Теперь максимизируйте или минимизируйте функцию, которую вы только что разработали. Вы будете использовать свои обычные инструменты исчисления, чтобы найти критические точки, определить, являются ли они максимальными или минимальными, и так далее. 93$.) Какие размеры (высота и радиус) минимизируют стоимость металла, необходимого для изготовления банки?

Этап I.

Разработка функции

Шаг 1.
В задачах оптимизации всегда начинайте с наброска ситуации . Всегда. По крайней мере, этот шаг означает, что вы смотрите не на чистый лист бумаги; вместо этого вы начали создавать свое решение.

Задача требует от нас минимизировать стоимость металла, используемого для изготовления банки, поэтому мы показали каждый кусок металла отдельно: круглую верхнюю часть банки, цилиндрическую сторону и круглое дно. Мы обозначили высоту банки h и его радиус r . Мы ищем значения h и r (в пересчете на V ), которые минимизируют стоимость изготовления банки.

Шаг 2.

Чаще всего вы будете использовать свои знания геометрии.

Нарисовав картинку, следующим шагом будет написать уравнение для величины, которую мы хотим оптимизировать . Чаще всего для этого шага вы будете использовать свои повседневные знания по геометрии. В этой задаче, например, мы хотим минимизировать стоимость изготовления банки, а это значит, что мы хотим использовать 92 + 2 \pi r h
\end{align*}

Вот и все; Вы сделали шаг 2! Вы написали уравнение для величины $(A_\text{total})$, которую хотите минимизировать, относительно соответствующих величин ( r и h ).

ДОПОЛНИТЕЛЬНЫЕ МАТЕРИАЛЫ

• Проблемы оптимизации и полные решения

Шаг 3.
Вот ключевой момент, который нужно знать о том, как решать проблемы оптимизации: вам почти всегда придется использовать подробную информацию, приведенную в задаче. до перепишите уравнение, которое вы разработали на шаге 2, чтобы оно использовало одну переменную.

Например, приведенное выше уравнение для $A_\text{total}$ имеет две переменные: r и h . Мы должны устранить одного из них, чтобы продолжить. Выбор того, что оставить, а что исключить, произволен; для нашего решения здесь мы решили сохранить r . (С тем же успехом мы могли бы выбрать ч и развивать наше решение по этому пути. Мы пришли бы к тому же конечному результату.) Поскольку мы решили работать с 92 + \frac{2V}{r}$$
Теперь мы пишем $A(r)$, чтобы подчеркнуть, что A является функцией только одной переменной r , и мы опустили нижний индекс « total» из $A_\text{total}$, так как он нам больше не нужен.

Это также завершает этап I нашей работы: за эти три шага мы разработали функцию, которую теперь собираемся минимизировать!

Заметьте, кстати, что до сих пор в нашем решении мы вообще не использовали Исчисление. Так будет всегда, когда вы решаете проблему оптимизации: вы не используете исчисление, пока не дойдете до стадии II.

Стадия II: максимизируйте или минимизируйте свою функцию

Многие учащиеся не понимают, что задача оптимизации на самом деле является задачей макс/мин.

Многие учащиеся не понимают, что задача оптимизации на самом деле является задачей макс/мин; это просто тот случай, когда вам сначала нужно разработать функцию, которую вы собираетесь максимизировать или минимизировать, как мы это сделали на этапе I выше. После этого оставшиеся шаги точно такие же, как и для задач на макс/минимум, которые вы недавно научились решать. 92 + \dfrac{710}{r}\,.$ Найдите значение r , которое минимизирует эту площадь».

Вероятно, вы автоматически нашли бы производную $A'(r)$ (которую вы могли бы эквивалентно записать как $\dfrac{dA}{dr})$, затем нашли критические точки, затем определили, представляет ли каждая из них максимум или минимум для функции и так далее. Это именно то, что мы сейчас собираемся сделать на Этапе II. Следовательно, вы уже знаете, как выполнить все следующие шаги; единственная новая часть задач максимизации — это то, что мы сделали на этапе I выше. 93 &= \frac{V}{2\pi} \\[8px]
r &= \sqrt[3]{\frac{V}{2\pi}}
\end{align*} \]
Таким образом, у нас есть только одна критическая точка для исследования, $r = \sqrt[3]{\dfrac{V}{2\pi}}\,. $

Шаг 5.
Далее мы должны обосновать, что Критическая точка, которую мы нашли, представляет минимум для площади поверхности банки (в отличие от максимума или седловой точки). Мы могли бы рассуждать физически или использовать тест первой производной, но мы думаем, что в этом случае проще всего использовать тест второй производной. Давайте быстро вычислим вторую производную, начиная с первой производной, которую мы нашли выше: 9\prime(r) > 0 \right)$. То есть график A(r) против r всегда вогнут вверх. Следовательно, эта единственная критическая точка дает нам минимум (в отличие от максимума или седловой точки), что и требуется:

Минимальная площадь поверхности возникает, когда $ r = \ sqrt [3] {\ dfrac {V {2\пи}}\,. \quad \triangleleft$

Шаг 6.
Теперь, когда мы нашли критическую точку, соответствующую минимальной площади поверхности банки (тем самым минимизируя стоимость), давайте 9{1/3}}\,\sqrt[3]{\frac{V}{\pi}} \\[8px]
&= 2 \sqrt[3]{\frac{V}{2\pi}} = 2r
\end{align*} \]
поскольку напомним, что идеальный радиус равен $r = \sqrt[3]{\dfrac{V}{2\pi}}\,. $ Следовательно, идеальная высота h ровно в два раза больше идеального радиуса.

Подводя итог, мы заключаем, что оптимальные размеры для банки с закрытой крышкой, которая должна содержать объем жидкости V , составляют
\[ \begin{align*}
\text{radius } r &= \sqrt[3 ] {\ dfrac {V} {2 \ pi}} \ quad \ cmark \\ [8px]
\text{высота} h &= 2\sqrt[3]{\dfrac{V}{2\pi}} \quad \cmark
\end{align*} \]

Шаг 7. Последняя проверка

Вы потеряете очки, если не ответите на заданный вопрос.

Поскольку решения по оптимизации могут быть длинными, мы рекомендуем, прежде чем закончить, вернуться и проверить, какое количество/количества запросила проблема, и убедиться, что вы предоставили это — , особенно на экзамене, где вы проиграете баллы, если вы не ответите точно на вопрос, который был задан. Например, задача 9.0020 мог бы запросить значение наименьшей возможной площади поверхности A или минимальную стоимость.

Вместо этого в этом случае задача гласила: «Какие размеры (высота и радиус) минимизируют стоимость металла для изготовления банки?» Мы обеспечили эти два измерения, и на этом мы закончили. $\checkmark$

Резюме: Стратегия решения проблем

Теперь мы проиллюстрировали шаги, которые мы используем для решения каждой отдельной проблемы оптимизации, с которой мы сталкиваемся, и они всегда работают.

СТРАТЕГИЯ РЕШЕНИЯ ЗАДАЧ: Оптимизация

Стратегия состоит из двух Больших Этапов. Первый вообще не связан с исчислением; второй идентичен тому, что вы сделали для задач max/min.

Этап I: Разработка функции.

Ваша первая задача — разработать функцию, представляющую количество, которое вы хотите оптимизировать. Это может зависеть только от одной переменной . Шаги:

1. Нарисуйте картину физической ситуации.
   Также обратите внимание на любые физические ограничения, определяемые физической ситуацией.
2. Напишите уравнение , которое связывает количество, которое вы хотите оптимизировать, с точки зрения соответствующих переменных.
3. При необходимости используйте другую предоставленную информацию, чтобы переписать уравнение с одной переменной.

Этап II: максимизация или минимизация функции.

Теперь вам нужно решить стандартную задачу на макс/мин.

4. Возьмем производную вашего уравнения относительно вашей единственной переменной. Затем найдите критические точки.
5. При необходимости определите максимумы и минимумы.
   Не забудьте проверить конечные точки , если они есть.
6. Обоснуйте свои максимумы или минимумы , либо рассуждая о физической ситуации, либо с помощью теста первой производной, либо с помощью теста второй производной.
7. Наконец, проверьте, правильно ли вы ответили на заданный вопрос : Перечитайте задачу и убедитесь, что вы предоставляете запрошенные значения: значение x или y ; или координаты; или максимальная площадь; или кратчайшее время; что бы ни спрашивали.

Хотите посмотреть, как мы решаем другие примеры задач?

Хотите посмотреть, как мы используем эту стратегию для решения других примеров задач? Перейдите на нашу страницу Оптимизация, чтобы увидеть больше примеров с бесплатными комплексными решениями.

А пока, к вам:

• Какими советами вы можете поделиться о том, как решить проблемы оптимизации?
• Какие у вас есть вопросы? Проблемы с оптимизацией могут быть сложными для начала, и мы будем рады помочь!
• Как мы можем сделать подобные сообщения более полезными для вас?

Пожалуйста, зайдите на наш форум и напишите!

[Спасибо С. Кэмпбеллу за его конкретное исследование обучения студентов оптимизации:

«Трудности студентов колледжа с прикладными задачами оптимизации в вводном исчислении», неопубликованная магистерская диссертация, Университет штата Мэн, 2013 г.]

Примеры задач оптимизации | Solr

Загрузить 119 примеров моделей сейчас

Оптимизация — это инструмент, который применяется во многих отраслях и функциональных областях. Чтобы узнать больше, зарегистрируйтесь, чтобы просмотреть избранные примеры онлайн по функциональным областям или отраслям. Вот полный список примеров моделей, к которым вы получите доступ после входа в систему. Вы можете запустить все эти модели с помощью базового решателя Excel.

Когда вы загрузите и установите бесплатную пробную версию наших усовершенствованных решателей для настольных компьютеров Microsoft Excel, вы обнаружите, что более девяноста (9)0) для вашего использования доступны небольшие, но полностью функциональные примеры моделей, охватывающие обычную оптимизацию, моделирование и анализ рисков, анализ решений (с использованием деревьев решений), оптимизацию с помощью моделирования, стохастическую оптимизацию и надежную оптимизацию. Вы можете сделать это в любое время после регистрации.

Примеры по функциональным областям

Корпоративные финансы

• Управление оборотным капиталом0030 : Инвестируйте в 1-месячные, 3-месячные и 6-месячные депозитные сертификаты, чтобы максимизировать проценты при удовлетворении потребности в наличных деньгах
   
• Планирование капиталовложений : Выберите комбинацию капитальных проектов, чтобы максимизировать общую NPV (чистую приведенную стоимость)
   
• Управление запасами : Сравните политики хранения запасов и повторного заказа с моделью EOQ (экономичный объем заказа)
   
• Управление денежными средствами : Определите, где разместить сейфы, чтобы свести к минимуму «плавающие» или процентные потери из-за задержек с почтой
   
• Планирование мощностей : определите, какие заводы следует открыть или закрыть

Инвестиции

• Оптимизация портфеля — Markowitz Model : Alling Funds на запасы для минимизирования для целевой ставки — с известной и невозможной.
• Управление портфелем акций : использует макрос VBA для оптимизации нескольких сценариев с минимальным риском при различных целевых нормах доходности, затем рисует график эффективной границы
   
• Оптимизация портфеля — модель Шарпа (CAPM) : использует функции регрессии Excel для расчета альф и бета акций по отношению к рыночному индексу, а затем использует их для поиска эффективного портфеля
   
• Управление портфелем облигаций : выделять средства на облигации, чтобы максимизировать доход, гарантируя, что дюрация портфеля равна инвестиционному горизонту до погашения — с известной или рассчитанной дюрацией
   
• Портфель облигаций Точное совпадение : Выделите средства на облигации, чтобы максимизировать доходность портфеля, обеспечивая при этом выполнение периодических обязательств — с реинвестированием или без него

Производство

• Продукт. : определить, сколько продуктов каждого типа из сборки от определенных частей до максимизации, в то время как недоступные части : vontestory inventory inventory inventory 9.0007  
• Распределение машин : Распределение производства продукта на разных машинах с различной производительностью, стоимостью запуска и эксплуатационными расходами для достижения производственных целей при минимальных затратах
   
• Смешивание : определить, какое сырье из разных источников смешивать для получения вещества с определенными желаемыми качествами при минимальных затратах
   
• Выбор процесса — Решите, какой из нескольких процессов (с различной скоростью, стоимостью и т. д.) следует использовать для производства желаемого количества продукта за определенное время с минимальными затратами
   
• Режущий материал : определить, как разрезать большие куски дерева, стали и т. д. на более мелкие куски желаемого размера, каждый из которых необходим в определенных количествах, чтобы свести к минимуму отходы =

Распространение

• Транспортная модель : определить, сколько продуктов на каждую заводя , чтобы свести к минимуму стоимость доставки при соблюдении складских требований и не превышая заводские поставки
   
• Многоуровневая, многотоварная транспортировка Модель : определите, сколько продуктов нескольких различных типов необходимо отправить с каждого завода на каждый склад и каждому клиенту, чтобы минимизировать общую стоимость доставки при удовлетворении спроса и не превышении мощностей и запасов
   
• Частичная загрузка — Решите, какие размеры или типы продуктов следует загружать в транспортное средство, учитывая его ограничения по размеру, чтобы наилучшим образом удовлетворить спрос или свести к минимуму неиспользуемое пространство
   
• Местоположение объекта : Определите, какие заводы (если таковые имеются) необходимо закрыть, чтобы свести к минимуму общие затраты, включая фиксированные эксплуатационные расходы и расходы на доставку между объектами
   
• Модель производства/транспортировки : определите, сколько продукции производить на каждом заводе и отгружать на склады и клиентам, чтобы минимизировать общие затраты при удовлетворении спроса, складских мощностей и фабричных поставок

Закупки

• Контракты позволяют указывать минимальные цены для каждого штата поставщикам, которые сделали ставки
   
• Хранение запасов/повторный заказ : сравнение политики складирования и повторного заказа с моделью EOQ (экономичный объем заказа)
   
• Медиа-планирование — Решите, сколько рекламы закупить в различных СМИ, чтобы минимизировать общие затраты при достижении целевого уровня охвата или частоты
   
• Закупки/транспортировка Модель : определите, сколько нужно закупить у разных поставщиков по заданным ценам, чтобы доставить из их мест на различные заводы, чтобы минимизировать общие затраты, включая затраты на покупку и доставку

Human Resources

• Планировка экипажа : rewing rews в разные авиационные сегменты, чтобы минимизировать общую стоимость, обеспечивая, что экипаж «Глова» и концы с конца
• Назначение офиса : Назначьте сотрудников в доступные офисы, чтобы максимально удовлетворить предпочтения сотрудников
   
• Планирование работы сотрудников : Планируйте сотрудников парка на еженедельные «смены» (пять рабочих дней плюс два последовательных выходных дня), чтобы минимизировать расходы на заработную плату при удовлетворении меняющегося спроса в каждый день недели, при необходимости с учетом стажа работы и предпочтений сотрудников
   
• Состав рабочей силы : Решите, сколько сотрудников необходимо переобучить, нанять и уволить, чтобы соответствовать изменяющимся требованиям к составу рабочей силы при минимизации затрат или текучести кадров
   
• Перемещение рабочей силы : Решите, сколько войск переместить из нескольких лагерей на несколько других баз, чтобы минимизировать время перемещения или общую стоимость

Examples by Industry

Airlines and Trucking

• Crew Scheduling :  Given a flight schedule, aircraft assignments, and restrictions в период дежурства наиболее эффективно распределять экипажи по рейсам
   
• Маршрутизация и назначение флота : Определите, какие самолеты будут летать по каждому маршруту, и последовательность сегментов, выполняемых каждым самолетом
   
• Управление доходами : для разных классов билетов определите, сколько мест нужно продать или оставить по мере приближения даты рейса

Нефть и газ

• Смешивание бензина : Из углеводородов с определенным октановым числом, давлением паров, летучестью и стоимостью определите, какое количество каждого из них необходимо смешать вместе для получения бензина обычного, среднего и высшего качества
   
• Покупка по контракту на газ : При прогнозируемом, но неопределенном спросе на газ определите, какие контракты покупать и сколько газа хранить в разное время
   
• Аукцион пропускной способности трубопровода : определите, какие заявки по разным ценам должны быть присуждены, чтобы максимизировать доход от продаж, не превышая при этом суточную пропускную способность трубопровода

.