А.В. Зыкина методы оптимизации. Методы оптимизации корнеенко
А.В. Зыкина методы оптимизации
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«Омский государственный технический университет»
Конспект лекций
Омск 2007
УДК 007(075)
ББК 32.81я73
З-96
Рецензенты:
О.В. Кириченова, канд. физ.-мат. наук, доц. ОмГПУ;
О.П. Диденко, канд. пед. наук, доц. ОмГИС
Зыкина, А.В.
З-96 Методы оптимизации: конспект лекций /А.В. Зыкина. – Омск: Изд-во
ОмГТУ, 2007. – 36 с.
В конспекте лекций приводятся основные теоретические сведения по линейной оптимизации. Излагается графический метод решения задачи линейного программирования, рассматриваются прямой и двойственный симплекс-методы, метод отсечений для задачи целочисленной оптимизации, метод потенциалов для решения транспортной задачи линейного программирования.
Конспект лекций предназначен для студентов специальности 230102 и направления подготовки 23010062.
Печатается по решению редакционно-издательского совета Омского государственного технического университета.
УДК 007(075)
ББК 32.81я73
Редактор Н.Н. Пацула
ИД № 06039 от 12,10,2001
Сводный темплан 2007 г.
Подписано к печати 20.02.07. Бумага офсетная.
Формат 6084 1/16. Отпечатано на дупликаторе.
Усл. печ. л. 2,25. Уч.-изд. л. 2,25
Тираж . экз. Заказ
Издательство ОмГТУ. 644050, г. Омск, пр-т Мира,11
Типография ОмГТУ
© А.В. Зыкина, 2007
© Омский государственный
технический университет, 2007
Введение
При решении широкого комплекса практических задач, в том числе задач создания и эксплуатации АСОИУ, возникают своеобразные модели оптимизации решений, для которых характерны следующие черты:
показатель эффективности (целевая функция) является линейной функцией от элементов решения;
ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств.
Такие задачи называются задачами линейного программирования (ЛП).
Первые исследования по ЛП были проведены в конце 30-х годов в Ленинградском университете академиком Л. В. Кантаровичем (первая публикация – в 1939 году). Л. В. Кантарович предложил легко алгоритмизируемый метод решения задач ЛП – метод последовательного улучшения допустимого вектора. Американский математик Дж. Данциг в 1947 году разработал симплекс-метод решения задачи ЛП. По существу симплекс-метод является табличной формой записи метода последовательного улучшения допустимого вектора. В 1951 году Дж. Данциг ввел термин «линейное программирование» (слово «программирование» в данном случае означает не что иное, как «планирование»).
В настоящее время, с точки зрения уровня теоретических разработок, сфера приложения и реализации вычислительных методов ЛП является одним из наиболее развитых направлений в области решения оптимизационных задач. Успехи в использовании методов ЛП во многом обусловлены значительным увеличением быстродействия и объема памяти ЭВМ. Достижения в области ЛП в свою очередь содействовали прогрессу в разработке алгоритмов решения других задач математического программирования. Сущность этих алгоритмов состоит в том, что исходная (в общем случае, нелинейная) задача сводится к одной линейной задаче или их совокупности. Таким образом, линейное программирование выделяется среди других методов программирования как основа для многих процедур решения.
При нахождении решений для моделей математического программирования (МП) применительно к реальным задачам процедуры ручного счета практически никогда не используются. Такого рода работа, как правило, осуществляется с помощью ЭВМ. Возникает вполне законный вопрос: не достаточно ли одного умения строить модели? Нет, не достаточно. Значительный опыт по использованию методов математического программирования при решении производственных задач подтвердил, что руководитель должен понимать принцип работы алгоритмов, чтобы добиться действительно эффективного и обоснованного применения этого инструмента организации управления. При практическом применении МП всегда стремятся получить более содержательную информацию, нежели ответ в числовом выражении. Главная цель расчетов – не цифры, а понимание.
studfiles.net
Самостоятельная работа 2 часа в неделю
министерство образования и науки российской федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Московский физико-технический институт (государственный университет)»
УТВЕРЖДАЮ
проректор по учебной работе
Ю.Н. Волков
«___» _____________ 20___ г.
П Р О Г Р А М М А
курса АНАЛИЗ МОДЕЛЕЙ И ОПТИМИЗАЦИЯ В УСЛОВИЯХ СТОХАСТИЧЕСКОЙ НЕОПРЕДЕЛЕННОСТИ
по направлению 010900 «Прикладные математика и физика»
по магистерским программам 010990
факультет управления и прикладной математики (ФУПМ)
кафедра предсказательного моделирования и оптимизации
курс IV
семестры 8 (весенний)
семинары нет зачёт дифф. 8 семестр (весенний)
лабораторные занятия нет
самостоятельная работа 2 часа в неделюВСЕГО ЧАСОВ 32
Программу составил: к.ф.-м.н. Дорофеев Е.А.
Программа обсуждена на заседании кафедры
предсказательного моделирования и оптимизации
14 марта 2011 года
Заведующий кафедрой
чл.-корр. РАН А.П. Кулешов
Программа обсуждена на заседании методического
совета ФУПМ 20 апреля 2011 года
Председатель методического совета
чл.-корр. РАН Ю.А. Флёров
1. Анализ источников неопределенности.
Эмпирические функции распределения. Методы ядерного сглаживания. Стандартные одно- и многомерные функции распределения. Анализ корреляций. Графический анализ с помощью QQ- графиков. Оценки параметров. Хи-квадрат тест. Тестирование по Колмогорову-Смирнову. Принцип максимального правдоподобия. Байесовские информационные критерии.
2. Вероятностные критерии качества и теория надежности. Аналитические методы.
Изовероятностные преобразования. Преобразование Розенблата. Преобразование Натафа. Точка наибольшей вероятности. Индекс надежности. Методы оценки надежности первого, второго и высших порядков (FORM, SORM, HORM). Проблема неединственности точки наибольшей вероятности.
3. Вероятностные критерии качества и теория надежности. Методы прямого компьютерного моделирования.
Методы пробных выборок. Различные разновидности метода Монте-Карло. Метод существенных выборок. Выборки направлений. Метод Латинского гиперкуба.
4. Оптимизация в условиях статистической неопределенности (робастная оптимизация).
Характеристика задач оптимизации в условиях неопределенности. Одноэтапная задача оптимизации. Двухэтапная задача оптимизации. Гибкость и стоимость исходной информации. Свойства функции гибкости.Метод множества активных ограничений. Метод ветвей и границ. Метод перебора. Функция потерь и функция вероятности. Функция квантили. Методы детерминированного эквивалента. Билинейная функция потерь и сферически симметричные распределения. Функция потерь возрастающая по стратегии. Аддитивная функция потерь. Метод эквивалентных преобразований. Доверительный метод. Максимизация целевых функций на доверительном эллипсоиде. Стохастические квазиградиентные алгоритмы. Задачи стохастического программирования с вероятностным ограничением.
5. Многокритериальная оптимизация в условиях неопределенности.
Скаляризация по Пасколетти-Серафини и её обобщения. Методы наискорейшего спуска и методы квази-Ньютона в многокритериальной оптимизации. Simulated annealing (SA) методы. Генетические алгоритмы. Множество Парето. Использование множества Парето для принятия решения. Обобщенный метод усредненного критерия. Метод последовательных уступок. Обобщенный метод Гермейера. Обобщенный метод ε-ограничений.
СПИСОК ЛИТЕРАТУРЫ
1. Боровков А.А. Математическая статистика: Оценка параметров. Проверка гипотез. М.: Наука, 1984.
2. Измайлов А.Ф., Солодов М.И. Численные методы оптимизации. М.: ФИЗМАТЛИТ, 2008.
3. Ермаков C.М. Метод Монте-Карло в вычислительной математике: вводный курс. М.: «БИНОМ. Лаборатория знаний» - СПб.: «Невский диалект», 2009.
4. Ермаков C.М. Статистическое моделирование: учебное пособие для вузов. М.: Наука, 1982. 296 с.
5. Соболь И.М. Численные методы Монте-Карло. М.: Наука, 1973.
6. Корниенко В.П. Методы оптимизации. М.: Высшая школа, 2007.
7. Поляк Б.Т. Введение в оптимизацию. М.: Наука, 1983.
8. Островский Г.М., Волин Ю.М. Технические системы в условиях неопределенности: анализ гибкости и оптимизация. М: БИНОМ. Лаборатория знаний, 2008.
9. Кан Ю.С., Кибзун А.И. Задачи стохастического программирования с вероятностными критериями. М.: ФИЗМАТЛИТ, 2009.
10. Ермольев Ю.М. Методы стохастического программирования. М.: Наука, 1976.
lib.znate.ru
Методы оптимизации.
32
Министерство образования Российской Федерации
Тольяттинский ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра «Автоматизация машиностроения»
Линейное программирование (ЛП).
Симплекс – метод решения задач ЛП.
Учебное пособие по дисциплине
«Основы САПР»
Тольятти 2003
УДК 002
Методы оптимизации. Линейное программирование (ЛП). Симплекс метод решения задач ЛП: Учебное пособие по дисциплине «Основы САПР»/ сост. Пиастро Г.П., Атлягузова Е.И., Коротыч В.И. - Тольятти: ТГУ, 2003.
Составители: Пиастро Г.П., Атлягузова Е.И., Коротыч В.И.
Научный редактор: Ройтбург Ю.С.
(с) Тольяттинский Государственный Университет, 2003
ОГЛАВЛЕНИЕ.
ВВЕДЕНИЕ. 4
1. Геометрическая интерпретация задачи. Анализ вариантов решений. 6
9
2. КАНОНИЧЕСКАЯ ФОРМА ПРЕДСТАВЛЕНИЯ ОГРАНИЧЕНИЙ. ДОПУСТИМЫЕ БАЗИСНЫЕ РЕШЕНИЯ. 10
3.СИМПЛЕКС-МЕТОД. АНАЛИЗ ПРОЦЕДУРЫ РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (С ПРИМЕРОМ). 12
4. ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ. 15
5. Прямой алгоритм симплексного метода 21
6. Прямой алгоритм с искусственными переменными 28
ВВЕДЕНИЕ.
Задача повышения эффективности технологических и организационных систем (например: металлорежущего станка, автоматической линии, производства в целом) путём принятия обоснованных решений актуальна во всех областях деятельности человека. Количественная оценка эффективности может быть получена при заданной цели функционирования системы, с учётом ограничений на ресурсы, привлекаемые для достижения цели. При этом задача принятия решения ставится как задача выбора параметров системы, обеспечивающих максимизацию или минимизацию целевой функции. Последняя количественно определяет степень достижения цели – величину критерия оптимизации. В качестве критерия можно принять, например, себестоимость изделия (цель-минимизация), быстродействие машины или прибора (цель-максимизация) и другие показатели.
Обоснованное применение количественных методов для принятия решений - оптимизацию поведения структур систем называют исследованием операций (ИСО). Здесь операция – комплекс целенаправленных действий.
Задача, рассмотренная выше, решается с применением математической модели системы, объединяющей упомянутые ограничения на ресурсы и целевую функцию. Нахождение величин упомянутых параметров системы (они входят в математическую модель как неизвестные) путём решения математической задачи называют математическим программированием. Математическое программирование – важнейшая область математики, ориентированная на широкое применение компьютеров. Одним из разделов этой области является линейное программирование.
В моделях линейного программирования так называемая «основная задача» состоит в нахождении неотрицательного решения системы линейных уравнений или неравенств (ограничений), которая минимизирует или максимизирует линейную форму (целевую функцию). Математическая задача линейного программирования записывается в сокращённом виде следующим образом:
найти 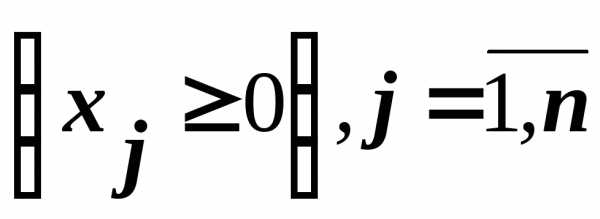
при ограничениях типа:
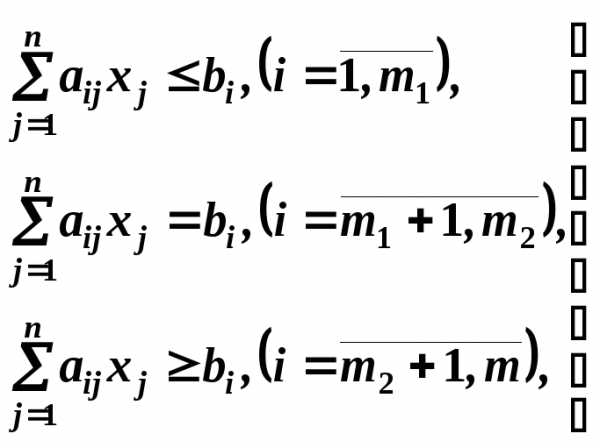 (0.1)
(0.1)
которые минимизируют (или максимизируют) линейную форму – целевую функцию:
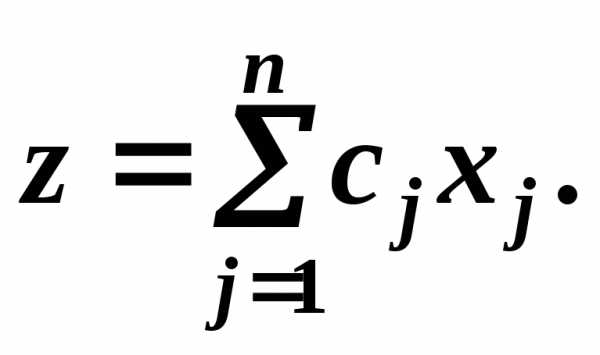 (0.2)
(0.2)
studfiles.net